性质
平衡二叉树(Balanced Binary Tree)又被称为AVL树(有别于AVL算法),除了具有二叉查找树的性质,还具有以下性质:
- 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,
- 并且左右两个子树也是平衡二叉树。
这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
平衡因子
一个节点的平衡因子就是该节点左子树的高度减去右子树的高度。
平衡二叉树上所有结点的平衡因子只可能是 -1,0,1。只要树上有结点的平衡因子的绝对值大于 1,则该二叉树就是不平衡的。
平衡调整的4种类型
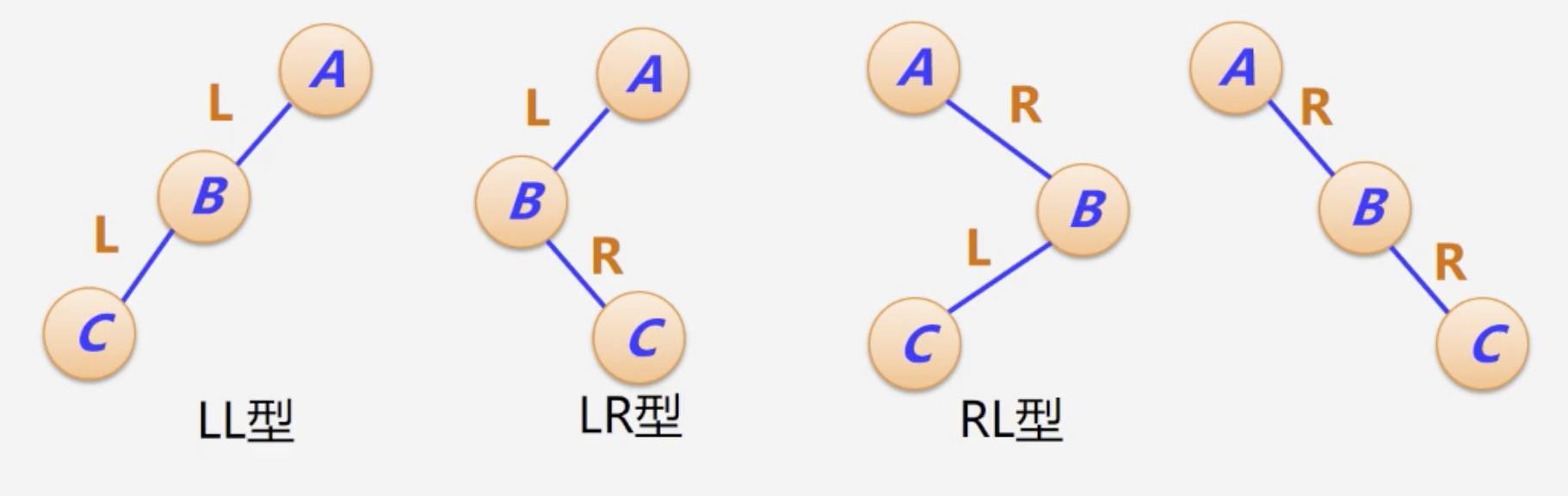
若因某个操作导致不平衡,则先找到离操作节点最近的平衡因子的绝对值大于1的节点A,再对以A为根的子树进行位置调整,使之重新达到平衡。

平衡二叉树的查找长度
假设以nh表示深度为h的平衡树中含有的最少节点数。显然有,n0=0,n1=1,n2=2,并且有nh=nh-1+nh-2+1。可以证明,含有n个节点的平衡二叉树的最大深度为O(log2n)。
代码实现
代码:
<?php
class AvlNode
{
public $key;
public $parent;
public $left;
public $right;
public $balanceFactor;
public function __construct($key)
{
$this->key = $key;
$this->parent = null;
$this->left = null;
$this->right = null;
$this->balanceFactor = AvlTree::EH;
}
}
class AvlTree
{
public $root;
const LH = 1;
const EH = 0;
const RH = -1;
private function inOrderTraverse($tree, $depth=0) // 注意 $tree 也可能是 null
{
if (!empty($tree)) {
$this->inOrderTraverse($tree->left, $depth + 1);
for ($i=0; $i < $depth; $i++) {
echo '-';
}
echo "{$tree->key}({$tree->balanceFactor})\n"; // --6(black)
$this->inOrderTraverse($tree->right, $depth + 1);
}
}
public function inOrder()
{
$this->inOrderTraverse($this->root);
}
private function searchNode(&$x, $key)
{
if (empty($x)) {
return '未找到'; // null
}
if($key < $x->key) {
return $this->searchNode($x->left, $key);
} elseif ($key > $x->key) {
return $this->searchNode($x->right, $key);
} else {
return $x->key;
}
}
public function search($key)
{
return $this->searchNode($this->root, $key);
}
/*
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋):
* px px
* / /
* x y
* / \ --(左旋)--> / \
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
private function leftRotate(AvlNode $x)
{
$y = $x->right;
$x->right = $y->left;
if (!empty($y->left)) {
$y->left->parent = $x;
}
$y->parent = $x->parent;
if (empty($x->parent)) { // $x 是根节点
$this->root = $y;
} else {
if ($x == $x->parent->left) { // $x 是其父亲的左孩子
$x->parent->left = $y;
} else { // $x 是其父亲的右孩子
$x->parent->right = $y;
}
}
$y->left = $x;
$x->parent = $y;
}
/*
* 对红黑树的节点(y)进行右旋转
*
* 右旋示意图(对节点y进行左旋):
* py py
* / /
* y x
* / \ --(右旋)-. / \
* x ry lx y
* / \ / \
* lx rx rx ry
*
*/
private function rightRotate(AvlNode $y)
{
$x = $y->left;
$y->left = $x->right;
if (!empty($x->right)) {
$x->right->parent = $y;
}
$x->parent = $y->parent;
if (empty($y->parent)) {
$this->root = $x;
} else {
if ($y == $y->parent->right) {
$y->parent->right = $x;
} else {
$y->parent->left = $x;
}
}
$x->right = $y;
$y->parent = $x;
}
private function calDepth($node)
{
if (empty($node)) {
return 0;
}
$left_depth = $this->calDepth($node->left);
$right_depth = $this->calDepth($node->right);
if($left_depth > $right_depth) {
return $left_depth + 1;
}
return $right_depth + 1;
}
public function getDepth($node)
{
return $this->calDepth($node);
}
// 左平衡处理
private function leftBalance(&$tree)
{
$lc = $tree->left; // 将成为新的“根”节点
switch ($lc->balanceFactor) {
case self::LH: // 新节点插入在 $tree 的左孩子的左子树上,作单右旋处理
$tree->balanceFactor = self::EH;
$lc->balanceFactor = self::EH;
$this->rightRotate($tree);
break;
case self::RH: // 新节点插入在 $tree 的左孩子的右子树上,作双旋处理(先左旋,后右旋)
$lc_rc = $lc->right;
switch ($lc_rc->balanceFactor) {
case self::LH:
$tree->balanceFactor = self::RH;
$lc->balanceFactor = self::EH;
break;
case self::EH:
$tree->balanceFactor = self::EH;
$lc->balanceFactor = self::EH;
break;
case self::RH:
$tree->balanceFactor = self::EH;
$lc->balanceFactor = self::LH;
break;
}
$lc_rc->balanceFactor = self::EH;
$this->leftRotate($tree->left);
$this->rightRotate($tree);
}
}
// 右平衡处理
private function rightBalance(&$tree)
{
$rc = $tree->right;
switch ($rc->balanceFactor) {
case self::RH:
$tree->balanceFactor = self::EH;
$rc->balanceFactor = self::EH;
$this->leftRotate($tree);
break;
case self::LH:
$rc_lc = $rc->left;
switch ($rc_lc->balanceFactor) {
case self::RH:
$tree->balanceFactor = self::LH;
$rc->balanceFactor = self::EH;
break;
case self::EH:
$tree->balanceFactor = self::EH;
$rc->balanceFactor = self::EH;
break;
case self::LH:
$tree->balanceFactor = self::EH;
$rc->balanceFactor = self::RH;
break;
}
$rc_lc->balanceFactor = self::EH;
$this->rightRotate($tree->right);
$this->leftRotate($tree);
}
}
private function insertAvl(&$tree, $node, &$taller)
{
if (empty($tree)) { // 插入新节点
$tree = $node;
$taller = true;
} else {
if ($node->key == $tree->key) {
$taller = false;
return false;
} elseif ($node->key < $tree->key) {
if (!$this->insertAvl($tree->left, $node, $taller)) {
return false; // 因关键字已存在,未插入
}
// 插入成功的话设置父指针
if (empty($tree->left->parent)) {
$tree->left->parent = $tree;
}
if ($taller) {
// 插入成功则$tree的左子树“长高”
switch ($tree->balanceFactor) {
case self::LH: // 原本左子树比右子树高,需要作左平衡处理
$this->leftBalance($tree);
$taller = false;
break;
case self::EH: // 原本左右子树等高,现左子树增高而使树增高
$tree->balanceFactor = self::LH;
$taller = true;
break;
case self::RH: // 原本右子树比左子树高,现在左右子树等高
$tree->balanceFactor = self::EH;
$taller = false;
break;
}
}
} else { // 对称处理即可
if (!$this->insertAvl($tree->right, $node, $taller)) {
return false;
}
if (empty($tree->right->parent)) {
$tree->right->parent = $tree;
}
if ($taller) {
switch ($tree->balanceFactor) {
case self::LH:
$tree->balanceFactor = self::EH;
$taller = false;
break;
case self::EH:
$tree->balanceFactor = self::RH;
$taller = true;
break;
case self::RH:
$this->rightBalance($tree);
$taller = false;
break;
}
}
}
}
return true;
}
public function insert($node)
{
$taller = false;
return $this->insertAvl($this->root, $node, $taller);
}
}
$AvlTree = new AvlTree();
$AvlTree->insert(new AvlNode(6));
$AvlTree->insert(new AvlNode(1));
$AvlTree->insert(new AvlNode(3));
$AvlTree->insert(new AvlNode(5));
$AvlTree->insert(new AvlNode(2));
$AvlTree->insert(new AvlNode(8));
$AvlTree->insert(new AvlNode(12));
$AvlTree->insert(new AvlNode(15));
$AvlTree->insert(new AvlNode(20));
$AvlTree->insert(new AvlNode(16));
echo '插入多个节点后的情况:', PHP_EOL;
$AvlTree->inOrder();
echo PHP_EOL;
echo '搜索关键字 15:', PHP_EOL;
print_r( $AvlTree->search(15) );
echo PHP_EOL;
echo '搜索关键字 30:', PHP_EOL;
print_r( $AvlTree->search(30) );
echo PHP_EOL;
输出:
插入多个节点后的情况:
-1(-1)
--2(0)
3(-1)
---5(0)
--6(0)
---8(0)
-12(0)
---15(0)
--16(0)
---20(0)
搜索关键字 15:
15
搜索关键字 30:
未找到