[数据结构与算法]Algorithm第四版算法 C++实现(九)——红黑树

红黑二叉查找树，简称红黑树。红黑树是2-3树的一种实现方法。

2-3树

所谓2-3树，就是 *2-节点（一个键与两条链接）与 3-节点（两个键与三条链接）的树
一颗完美平衡的2-3树所有空连接到根根节点的距离应该是相同的
由于2-3树的插入代码比较复杂，我在此就不再赘述了，有兴趣的读者可以查阅相关资料
由于实现2-3树的代码非常复杂，而且其产生的大量额外开销使得2-3树甚至比普通的二叉树更慢。所以我们必须使用更高效的方式实现他们。于是红黑树就出现了

红黑树

红黑树就是用普通二叉树与一些额外信息来表示2-3树：红链接将两个2-结点连接成一个3-节点，黑链接表示普通链接

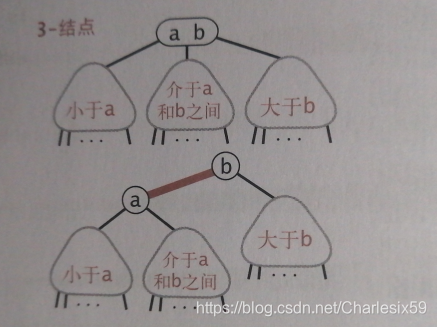
红黑树需要满足的条件：

1. 红链接均为左连接
2. 没有任何一个节点同时和两条红链接相连
3. 树是完美黑色平衡的，即任意空链接到根节点路径上的黑链接数量相同

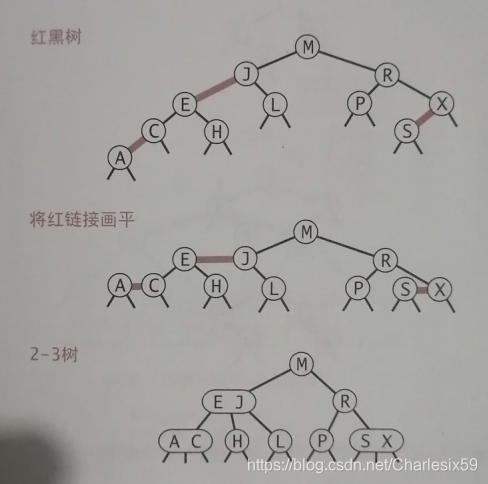
我们可以将红链接画平，如图

要使得红黑树具有上述性质，我们需要在插入新节点后对树节点进行旋转来配平。因为旋转的方式并不容易理解，我此处就不多赘述了，可以参考一些动态图或者视频来理解红黑树的旋转。（类似的旋转在AVL的构造中也会出现，但书中貌似并未提到普通的AVL）
我们可以直接使用标准二叉树的get等方法。所以此处我就不在列出了，请去上去查看get()的代码。你甚至可以把红黑树作为二叉树的一个子类（感兴趣的朋友可以尝试这种类继承的方式）

template<typename T,typename V>
class RBT
{
public:
	void put(T key, V value)
	{
		root = put(root, key, value);
		root->color = black;
	}
private:
	const bool red = true;
	const bool black = false;
	struct node
	{
		T key;
		V value;
		node *left;
		node *right;
		int n;
		bool color;
	};
	node *root;
	node *create_node(T key, V value, int n, bool color)
	{
		node *newnode = new node;
		newnode->key = key;
		newnode->value = value;
		newnode->n = n;
		newnode->color = color;
		newnode->left = nullptr;
		newnode->right = nullptr;
		return newnode;
	}
	bool is_red(node *x)
	{
		if (x == NULL)
			return false;
		return x->color;
	}
	int size(node *x)
	{
		if (x == NULL)
			return 0;
		else
			return x->n;
	}
	void rotate_left(node *h)
	{
		node *x = h->right;
		h->right = x->left;
		x->left = h;
		x->color = h->color;
		h->color = red;
		x->n = h->n;
		h->n = 1 + size(h->left) + size(h->right);
	}
	void rotate_right(node *h)
	{
		node *x = h->left;
		h->left = x->right;
		x->right = h;
		x->color = h->color;
		h->color = red;
		x->n = h->n;
		h->n = 1 + size(h->left) + size(h->right);
	}
	void flip_color(node *h)
	{
		h->color = red;
		h->left->color = black;
		h->right->color = black;
	}
	node *put(node *h, T key, V value)
	{
		if (h == nullptr)
			return create_node(key, value, 1, red);
		if (key < h->key)
		{
			h->left = put(h->left, key, value);
		}
		else if (key > h->key)
		{
			h->right = put(h->right, key, value);
		}
		else
		{
			h->value = value;
		}
		if (is_red(h->right) && !is_red(h->left))
		{
			rotate_left(h);
		}
		if (is_red(h->left) && is_red(h->right))
		{
			rotate_right(h);
		}
		if (is_red(h->right) && is_red(h->left))
		{
			flip_color(h);
		}
		h->n = size(h->left) + size(h->right) + 1;
		return h;
	}
};