贪心算法
1. “455. 分发饼干”
先对饼干和胃口进行升序排序,
这里的局部最优就是小饼干喂给胃口小的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
如果没有喂饱,则换下一个饼干,
如果喂饱了,则用下一个饼干喂下一个孩子
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int ans = 0;
int j = 0;
for (int i = 0; i < s.length; i++) {
if (j == g.length) {
break;
}
if (g[j] <= s[i]) {
ans++;
j++;
}
}
return ans;
}
}
2. “1005. K 次取反后最大化的数组和”

贪心的思路,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。局部最优可以推出全局最优。
先对数组进行升序排序,然后把最大的负数依次变为正数。
如果此时还有取反次数,但是所有负数已经全部变为正数了,那就将绝对值最小的数进行取反,直到取反次数等于k。
因为这个数组是升序排序的,因此当nums[i]大于等于0时,绝对值最小的数一定是nums[i]或者是nums[i-1],也就是0的左右两个数一定是绝对值最小的
class Solution {
public int largestSumAfterKNegations(int[] nums, int k) {
Arrays.sort(nums);
for (int i = 0; i < k; i++) {
if (nums[i] < 0) {
nums[i] = -nums[i];
} else {
int j = i;
while (j++ < k) {
if (i - 1 > -1 && Math.abs(nums[i]) > Math.abs(nums[i - 1])) {
nums[i - 1] = -nums[i - 1];
} else {
nums[i] = -nums[i];
}
}
break;
}
}
int ans = 0;
for (int i : nums) {
ans += i;
}
return ans;
}
}
3. “860. 柠檬水找零”
有如下三种情况:
情况一:账单是5,直接收下。
情况二:账单是10,消耗一个5,增加一个10
情况三:账单是20,优先消耗一个10和一个5,如果不够,再消耗三个5
class Solution {
public boolean lemonadeChange(int[] bills) {
int five = 0;
int ten = 0;
int twenty = 0;
for (int i = 0; i < bills.length; i++) {
if (bills[i] == 10) {
if (five == 0) {
return false;
}
five--;
ten++;
} else if (bills[i] == 20) {
if (ten >= 1 && five >= 1) {
ten--;
five--;
twenty++;
} else if (five >= 3) {
five -= 3;
twenty++;
} else {
return false;
}
} else {
five++;
}
}
return true;
}
}
序列问题
4. “376. 摆动序列”

https://leetcode-cn.com/problems/wiggle-subsequence/solution/376-bai-dong-xu-lie-tan-xin-jing-dian-ti-vyxt/
class Solution {
public int wiggleMaxLength(int[] nums) {
int curDiff = 0;
int preDiff = 0;
int ans = 1;
for (int i = 1; i < nums.length; i++) {
curDiff = nums[i] - nums[i - 1];
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
ans++;
preDiff = curDiff;
}
}
return ans;
}
}
5. “738. 单调递增的数字”
题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]–,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
这一点如果想清楚了,这道题就好办了。
局部最优:遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]–,然后strNum[i]给为9,可以保证这两位变成最大单调递增整数。
全局最优:得到小于等于N的最大单调递增的整数。
但这里局部最优推出全局最优,还需要其他条件,即遍历顺序,和标记从哪一位开始统一改成9。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
所以从前后向遍历会改变已经遍历过的结果!
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
class Solution {
public int monotoneIncreasingDigits(int n) {
String s = String.valueOf(n);
char[] ch = s.toCharArray();
int k = -1;
for (int i = s.length() - 1; i > 0; i--) {
if (ch[i] - '0' < ch[i - 1] - '0') {
ch[i - 1] = Character.forDigit(ch[i - 1] - '1', 10);
k = i;
}
}
if (k == -1) {
return n;
}
for (int j = k; j < s.length(); j++) {
ch[j] = '9';
}
return Integer.valueOf(String.valueOf(ch));
}
}
股票问题
6. “122. 买卖股票的最佳时机 II“

买卖多次获得最大利润可以通过计算大于0的所有利润之和来获得
class Solution {
public int maxProfit(int[] prices) {
int ans = 0;
for (int i = 1; i < prices.length; i++) {
ans += Math.max(prices[i] - prices[i - 1], 0);
}
return ans;
}
}
7. ”714. 买卖股票的最佳时机含手续费“
两个维度权衡问题
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。如果两个维度一起考虑一定会顾此失彼。
8. “135. 分发糖果”
使用一个数组记录每个孩子分到的糖果数量,并且每个孩子至少一个糖果,数组初始化为1。
题目要求评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果,
也就是说评分更高的孩子比左边孩子的糖果数要多一个,并且比右边孩子的糖果数也要多一个。
因此,进行两次遍历,第一次从左往右,使得评分更高的孩子比左边孩子的糖果数多一个,
第二次从右往左,使得评分更高的孩子比右边的孩子的糖果数多一个。需要注意的是,第二次遍历时,得分更高的孩子的糖果数有可能要比右边的孩子的糖果数要多不止一个,那么此时糖果数是不变的,也就是Math.max(candy[i] + 1, candy[i - 1])
为什么第二次要从右往左呢?
因为第二次遍历是右边孩子的糖果数+1,因此需要依赖右边的数值,所以从右往左
class Solution {
public int candy(int[] ratings) {
int ans = 0;
int[] candy = new int[ratings.length];
Arrays.fill(candy, 1);
for (int i = 1; i < ratings.length; i++) {
if (ratings[i] > ratings[i - 1]) {
candy[i] = candy[i - 1] + 1;
}
}
for (int i = ratings.length - 1; i > 0; i--) {
if (ratings[i - 1] > ratings[i]) {
candy[i - 1] = Math.max(candy[i] + 1, candy[i - 1]);
}
}
for (int i : candy) {
ans += i;
}
return ans;
}
}
9. “406. 根据身高重建队列”
https://leetcode-cn.com/problems/queue-reconstruction-by-height/solution/406du-shuo-shi-tan-xin-na-yao-wei-shi-yao-yong-tan/
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
if (a[0] == b[0]) {
return a[1] - b[1];
}
return b[0] - a[0];
}
});
List<int[]> ans = new LinkedList<>();
for (int[] p : people) {
ans.add(p[1], p);
}
return ans.toArray(new int[people.length][2]);
}
}
区间问题
10. ”55. 跳跃游戏“
这个问题就是求所能达到的最大区间,只要每次都选择区间内的最大区间就可以了。
局部最优解就是选择局部最大区间
全局最优解就是局部最大区间是否能达到数组最后一个数
class Solution {
public boolean canJump(int[] nums) {
if (nums.length == 1) {
return true;
}
int maxRange = nums[0];
for (int i = 0; i <= maxRange; i++) {
maxRange = Math.max(maxRange, i + nums[i]);
if (maxRange >= nums.length - 1) {
return true;
}
}
return false;
}
}
11. “45. 跳跃游戏 II”
这题和上一题最大的区别就是,这题需要在每次可以跳跃的区间内选择最大的,而上一题是遇到更大的区间就跳
class Solution {
public int jump(int[] nums) {
if (nums.length == 1) {
return 0;
}
int curRange = 0;
int nextRange = 0;
int ans = 0;
for (int i = 0; i < nums.length - 1; i++) {
nextRange = Math.max(nextRange, nums[i] + i);
if (i == curRange) {
curRange = nextRange;
ans++;
}
}
return ans;
}
}
12. “452. 用最少数量的箭引爆气球”
先来分析题目,要求用最少的箭射最多的气球,也就是求气球的最大公共区间,因此局部最优解就是气球的最大公共区间,全局最优解就是有几个不同的公共区间。
接下来的问题就是如何求气球的最大公共区间,
首先对气球的左区间进行从小到大排序,然后就依次查看右区间能否覆盖下一个气球,也就是右区间是否大于等于下一个气球的左区间,如果大于等于,说明可以覆盖,右区间更新为当前右区间和被覆盖的气球的右区间的最小值。
如果小于,说明不能覆盖,则两者无公共区间,右区间更新为下一气球的右区间,ans+1。
画个图就很清楚了
class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
if (a[0] == b[0]) {
return a[1] - b[1];
}
return Long.compare(a[0], b[0]);
}
});
int ans = 1;
int right = points[0][1];
for (int i = 1; i < points.length; i++) {
if (points[i][0] <= right) {
right = Math.min(right, points[i][1]);
} else {
right = points[i][1];
ans++;
}
}
return ans;
}
}
13. “435. 无重叠区间”
首先将数组进行排序,将区间大的放在后面,比如说[1,2][2,3][1,3],[1,3]的区间比[1,2][2,3]更大,也就是说排序之后如果存在重叠区间,最大的父区间一定是在它包含的子区间后面的。就是这样[子区间][子区间][父区间],比如说[1,2][2,3][1,3]。
排好序后问题就简单了,要做的就是判断是否存在重叠区间,当前区间的左边大于等于上一个区间的右边就代表无重叠,更新右边界。
否则代表有重叠,有重叠就将这个区间删除,但是我们没有必要真的去做删除的逻辑,而是将这个区间给忽略掉,也是相当于删除了,也就是说当有重叠时,右边界还是不变的。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length < 2) {
return 0;
}
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
if (a[1] == b[1]) {
return b[0] - a[0];
}
return a[1] - b[1];
}
});
int right = intervals[0][1];
int ans = 0;
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] >= right) {
right = intervals[i][1];
} else {
ans++;
}
}
return ans;
}
}
14. “763. 划分字母区间”
先分析题目,题目要求把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
说白了也就是区间问题,将字母装换为区间,就是在求不重合的区间罢了。
比如说"ababcbacadefegdehijhklij"装换为区间
/**
a:0-8
b:1-5
c:4-7
d:9-14
e:10-15
f:11-11
g:13-13
h:16-19
i:17-22
j:18-23
k:20-20
l:21-21
*/
首先利用LinkedHashMap来存储字符和对应的区间数组,为什么要用LinkedHashMap呢?这是因为我们后续判断不重合区间是需要升序来进行的。
然后遍历map,找到不重合的区间并记录下标。
class Solution {
public List<Integer> partitionLabels(String s) {
List<Integer> ans = new ArrayList<>();
Map<Character, int[]> map = new LinkedHashMap<>();
int sLen = s.length();
for (int i = 0; i < sLen; i++) {
char ch = s.charAt(i);
if (!map.containsKey(ch)) {
map.put(ch, new int[]{i,i});
} else {
map.get(ch)[1] = i;
}
}
int left = -1;
int right = -1;
int pre = 0;
for (int[] arr : map.values()) {
if (left == -1 && right == -1) {
left = arr[0];
right = arr[1];
continue;
}
if (arr[0] > right) {
ans.add(arr[0] - pre);
pre = arr[0];
}
right = Math.max(right, arr[1]);
}
ans.add(right - pre + 1);
return ans;
}
}
15. “56. 合并区间”

虽然这是一道常规的区间问题,但是它的解题方法还是非常巧妙的。
首先按照左边界升序排序,
然后遍历数组,当是第一个数组元素或者左边界大于list中最后一个元素的右边界时(也就是无重叠),将这个元素加入到list中,
如果左边界小于list中最后一个元素的右边界时(也就是有重叠),将list中最后一个元素的右边界改为当前元素右边界(如果当前元素右边界小于list中最后一个元素的右边界,则不变)。
该题利用了在list中区间的有序性,并对最后一个区间进行修改,这个思路还是非常巧妙的
class Solution {
public int[][] merge(int[][] intervals) {
if (intervals.length == 1 || intervals.length == 0) {
return intervals;
}
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] a, int[] b) {
return a[0] - b[0];
}
});
List<int[]> ans = new ArrayList<>();
for (int i = 0; i < intervals.length; i++) {
int left = intervals[i][0];
int right = intervals[i][1];
if (i == 0 || left > ans.get(ans.size() - 1)[1]) {
ans.add(new int[]{left, right});
} else {
ans.get(ans.size() - 1)[1] = Math.max(ans.get(ans.size() - 1)[1], right);
}
}
return ans.toArray(new int[ans.size()][]);
}
}
其他
16. “53. 最大子序和”

贪心贪的是哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
class Solution {
public int maxSubArray(int[] nums) {
int cur = 0;
int max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
cur += nums[i];
if (cur > max) {
max = cur;
}
if (cur <= 0) {
cur = 0;
}
}
return max;
}
}
17. “134. 加油站”
可以换一个思路,首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,再从0计算curSum。
目标就是找出rest[i]大于0的区间的起始位置,并且rest[i]一定是i~length-1这个范围内的。
两个问题:
-
rest[i]大于0的区间有什么意义?
首先,rest[i]代表了i~length-1这个范围内的剩余油量,因此rest[i]大于0就说明从这个区间开始走,一定是可以开往下一个区间的 -
为什么rest[i]的起始位置就一定是出发的位置?
首先需要明确的是,因为这个起始位置剩余油量一定是大于0的,然后前面的区间油量之和一定是小于0的,并且总油量之和一定是大于等于0的,只有加上了这个起始位置,才使得总油量之和大于等于0
https://leetcode-cn.com/problems/gas-station/solution/shou-hua-tu-jie-liang-ge-guan-jian-jie-lun-de-jian/
https://leetcode-cn.com/problems/gas-station/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-tan-x-f3cv/
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int cur = 0;
int max = 0;
int ans = 0;
for (int i = 0; i < gas.length; i++) {
cur += gas[i] - cost[i];
max += gas[i] - cost[i];
if (cur < 0) {
cur = 0;
ans = i + 1;
}
}
if (max < 0) {
return -1;
}
return ans;
}
}
18.“968. 监控二叉树”
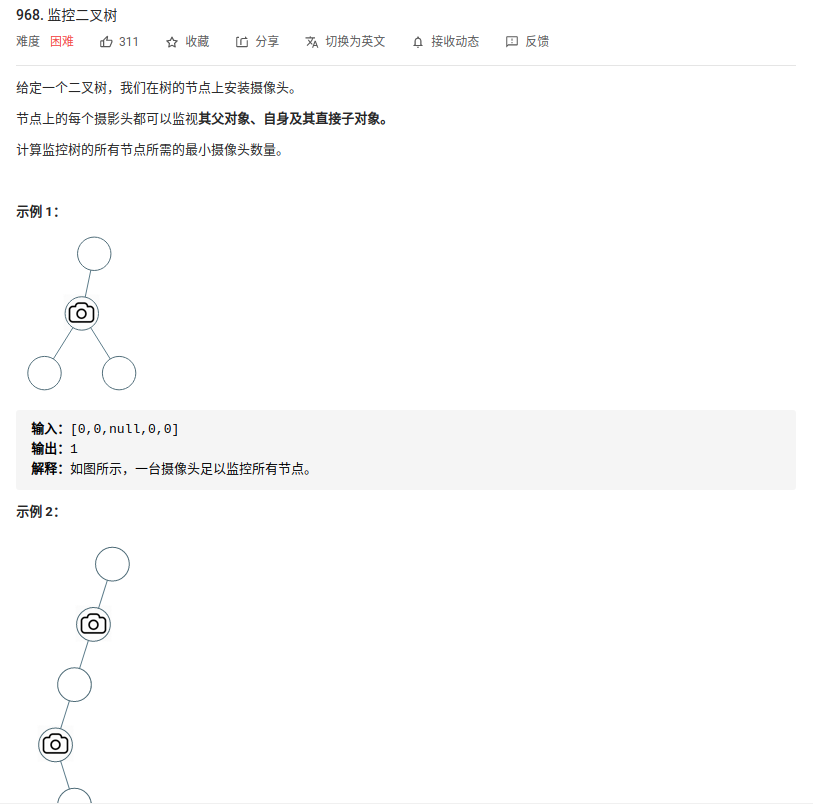
根据题意可知,每个节点有三种状态:
0. 状态0代表空节点或者是照相机节点的父节点
- 状态1代表状态0的父节点,照相机节点的子节点
- 状态2代表照相机节点
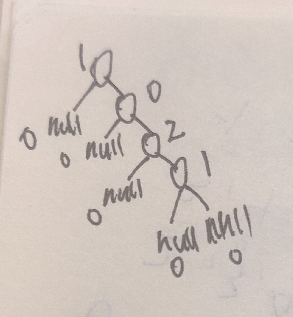
并且判断的优先级也需要注意,首先肯定是状态为1的节点优先,因为如果1不优先则会造成有节点没有被监控的情况,其次是状态为2,这是为了不重复监控
class Solution {
private int ans = 0;
public int minCameraCover(TreeNode root) {
if (dfs(root) == 1) {
return ans + 1;
}
return ans;
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int left = dfs(root.left);
int right = dfs(root.right);
if (left == 1 || right == 1) {
ans++;
return 2;
} else if (left == 2 || right == 2) {
return 0;
} else if (left == 0 || right == 0) {
return 1;
}
return 0;
}
}