动态规划可以简单地理解为对传统递归的一种优化。Dynamic Programming不是编程，而是决策。只是这种决策不是一下就出来的，而是一步步(multistage)积累出来。换句话说我们需要一个决策，但这个决策太大了，我们做不了，所以需要把他递归到我们可以简单做出决策的状态，然后从这些状态开始，慢慢的“动态地”演进到最终的决策。

比如说用最少的硬币换零钱？

突然和你说要换78分钱，你怎么就能迅速给出答案呢，你不能。但是如果是1分的话，你就可以，2分的话呢，就是在1分的基础上再加1分，你也可以。于是你就慢慢地从1分开始一直算到78就有答案了。从另一个角度说，如果你用DP算出了怎么换78分，那如果我问你76分怎么换，你也应该有答案了。

所以，DP在实践中很重要的就是递推关系和边界条件。

已知问题规模为n的前提A，求解一个未知解B。（我们用An表示“问题规模为n的已知条件”）

此时，如果把问题规模降到0，即已知A0，可以得到A0->B.

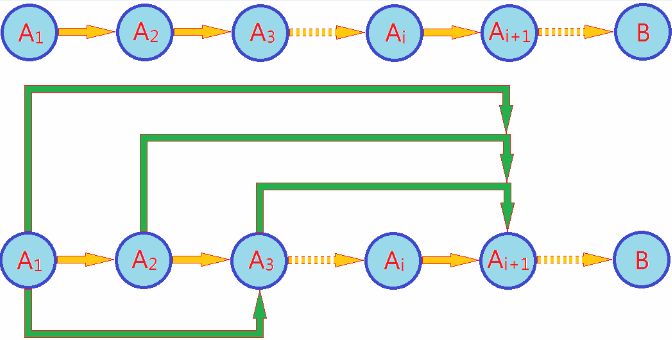
如果从A0添加一个元素，得到A1的变化过程。即A0->A1; 进而有A1->A2; A2->A3; …… ; Ai->Ai+1. 这就是严格的归纳推理，也就是我们经常使用的数学归纳法；
对于Ai+1，只需要它的上一个状态Ai即可完成整个推理过程（而不需要更前序的状态）。我们将这一模型称为马尔科夫模型。对应的推理过程叫做“贪心法”。

然而，Ai与Ai+1往往不是互为充要条件，随着i的增加，有价值的前提信息越来越少，我们无法仅仅通过上一个状态得到下一个状态，因此可以采用如下方案：

{A1->A2}; {A1, A2->A3}; {A1,A2,A3->A4};……; {A1,A2,...,Ai}->Ai+1. 这种方式就是第二数学归纳法。???????
对于Ai+1需要前面的所有前序状态才能完成推理过程。我们将这一模型称为高阶马尔科夫模型。对应的推理过程叫做“动态规划法”。

上述两种状态转移图如下图所示：

1.1 使用动态规划的条件

该问题是否能用动态规划解决的是可以分为多个相关子问题，这些”小问题“会不会被被重复调用。而不是一个“大问题”能够被拆解为一堆“小问题”

举个例子，有n个阶梯，一个人每一步只能跨一个台阶或是两个台阶，问这个人一共有多少种走法？

首先对这个问题进行抽象，n个阶梯，每个阶梯都代表一个“位置”，就像是图论中的一个“点”，然后这n个不同位置之间会有一些桥梁把它们连接起来。==>也可以写成列表形式，或邻接矩阵。

idea：如果是暴力遍历的话，从3到10的时候，你肯定会把5-10的可能路径都算一遍，然后从4-10的时候，你又会把5-10的路径算一遍，也就是重复计算了。

solve：创建一个数组a[]，专门来存放位点x到10的所有可能路径数。?

?a[5] = a[6] + a[7]

a[4] = a[5] + a[6] ? ? ? ? ? ? ? ? 数学归纳法？

.......

a[x] = a[x+1] + a[x+2]

我们发现在计算a[4]和a[5]的时候，都用到了a[6]，也就是重复利用了结果。

==>换句话说，如果从6-10的最优路径确定了，那无论是从3、4、5开始的路径，凡是再次到达6，那么从6往后的最优路径就不用再重复计算了。?

1.2 应用动态规划的步骤

(1) 按顺序从小到大计算。因为如果直接让你计算f(11)，你肯定一脸懵逼，但f(0), f(1)你却能很快理解，发现规律

(2) 建立状态转移方程。求得f(n)表达式

(3) 缓存以往结果以复用。比如刚刚求得f(99)，如果不将其缓存起来，那么求f(100)时，我们就必须重新从头计算。?

1.3 DP和贪心算法区别

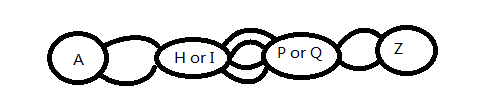
?贪心：如果第一步到H和I都可以，第二步到P和Q都可以，那我每一步只选最优，用贪心得到结果。<== 因为你要经历的每个阶段状态跟决策无关，即每个阶段状态相互独立，互不影响。

但现实情况是，你第一步的选择会影响后面的分支。?

比如你第一步选择H或I，但是到了H后，你就只能选择经过P或Q到Z了，而如果到了I，你只能选择R或S到Z。

这样一来，即便第一步到H或I你选择了较好的一条路，也不保证最终结果最优。?

==> 所以我们要把所有的路都尝试一遍，才知道哪个最优。-->穷举

但我们只需要计算到每个共有状态的位置，求各阶段的最优，最后每阶段选最优组合贪心组合起来就行，因为共有状态不影响决策，即不影响最终最优路径选择。对A->H->Q->Z和A->I->Q->Z，Q->Z是共有状态。Q->Z的最优可减少每条经过Q的最优路径的重复计算，当然可能存在A->H->Z路径比任何一条经过Q的路径更短，但我们说的是减少经过Q往后的路径的重复计算。?

1.4 DP和递归区别

1.4.1 斐波那契递归实现

# 递归实现
def fib_re(n):
    if n < 2:
        return n
    else:
        return fib_re(n-1) + fib_re(n-2)
    # 递归实现fib(100)时间太长，我出去打个电话都没运算完，而动态规划fib(100)秒算

if __name__ == '__main__':
    result = fib_re(100)
    print(result)

递归这种方式造成栈空间极大浪费！！！?

其指数级时间复杂度 $O(2^{n})$ 跟不能用没啥区别！！！出个打个20分钟的电话都没结束

1.4.2 斐波那契动态规划实现

# 动态规划实现
def fib_DP(n):
    results = list(range(n+1))
    for i in range(n+1):
        if i < 2:
            results[i] = i
        else:
            results[i] = results[i-1] + results[i-2]
    return results[n]


if __name__ == '__main__':
    result = fib_DP(100)
    print(result)

秒算?