图的基础
在线性表中,数据元素之间存在线性关系,每个元素存在前驱和后继结点;在树结构中,数据元素之间存在层次关系,并且一个结点可能和下一层次结点存在一对多的关系;而在图结构中,结点之间的关系可以是任意的,符合现实中很多事物之间的关系。
- 图的定义:图G=<V,E>(V vertex 顶点集,E edge 边集)。E可以为空,那时G只有顶点。
- 图的分类:有向图(边都为有向边)和无向图(边都为无向边)。<x,y>x为有向边起点,y为终点;<x,y>又称弧,x为弧尾,y为弧头。
- 图的术语(n,顶点数目;e,边的数目)
- 子图:G(V,E)和G1(V1,E1),V1和E1分别包含于V和E,称G1为G的子图。
- 无向完全图和有向完全图:无向图满足e=n*(n-1)/2(n的结点两两成边的组合);有向图满足e=n*(n-1)(n的结点两两成边的排列)
- 权和网:边带边权值,可以表示为两个顶点的距离或消耗。这样带权的图被称为网
- 邻接点:无向图G,存在边<v,v1>,那么v和v1互为邻接点,边和这俩顶点相关联。
- 度、出度和入度:顶点的度为与该顶点相关联的边的数目。入度为该顶点为弧头的边的数目,相对应,出度为顶点为弧尾的边的数目。e为各顶点度的和的1/2。
- 路径和路径长度:一个顶点到另一个顶点经过的顶点序列。路径长度为路径上边或弧的数目。
- 回路或环:路径中第一个顶点和最后一个顶点相同。
- 简单路径、简单环:路径中不存在重复顶点。
- 连通:顶点v到v1存在路径。
- 无图中从每一个顶点到另一个顶点都存在路径被称为连通图。若整个图不满足但是极大连通子图满足,被称为连通分量;若为有向图,称为强连通图。类似的,满足的条件的极大连通子图被称为强连通分量。
- 连通图的生成树:一个极小连通子图,含有全部n的顶点,和足以构成一棵树的n-1个边。如下图表示的一颗生成树。
- 有向树和生成森林:有一个顶点入度为0,其他顶点的入度都为1的有向图被称为有向树。一个有向图的生成树由若干树组成。
~如图左边的有向图和右边的生成树
图的存储结构
邻接矩阵
存储思想
因为图的任意两个顶点之间可能存在关系,所以一个G含有n个顶点,可以用n阶矩阵来表示顶点之间邻接关系,也称邻接矩阵。
如果图中存在<i,j>这条弧:
- 如果是有向图,致矩阵aij = 1,否则为0;
- 同理可知无向图的矩阵为对称矩阵,aij = aji = 1;
- 若是网,那么致aij = wij ,否则为无穷大。
下图为有向网的邻接矩阵
代码
邻接矩阵的实现采用,一个顶点集,一个边集来存储表示。
///GAmatrix.h
#pragma once
#include<stdio.h>
#define Maxint 32767
#define MAX 10
//类型定义
typedef char VertexType;
typedef int Edgetype;
//邻接表定义
typedef struct {
VertexType V[MAX]; //顶点集
Edgetype E[MAX][MAX]; //边集
int n, e;
}G_Amatreix;
//创建图
void CreateG(G_Amatreix& g);
//找到顶点在顶点集中的标号
int LocateV(G_Amatreix g, VertexType v);
函数实现
#include<stdio.h>
#include"GAmatrix.h"
/// ===============================================
/// 图接口实现
/// ===============================================
//创建图
void CreateG(G_Amatreix& g) {
printf("input n , e:\n");
scanf_s("%d,%d", &g.n, &g.e);
getchar();
//初始化V
for (int i = 0; i < g.n; ++i) {
printf("input V[%d]:", i);
scanf_s("%c", &g.V[i], 1);
char ch = getchar();
while (ch != '\n')
ch = getchar();
}
//初始化E
for (int i = 0; i < g.n; ++i) {
for (int j = 0; j < g.n; ++j) {
g.E[i][j] = Maxint; //创立网是为无穷大,图时为0
}
}
//输入边
char v1 = 0, v2 = 0;
int m = 0;;
int j, k;
for (int i = 0; i < g.e; ++i) {
printf("input the edge:(v1 v2 w)\n");
scanf_s("%c %c %d", &v1, 1, &v2, 1, &m);
char ch = getchar();
while (ch != '\n')
ch = getchar();
j = LocateV(g, v1);
k = LocateV(g, v2);
g.E[j][k] = m; //创立网时为权值w,图时为1
g.E[k][j]=g.E[j][k]; //无向时为对称矩阵
}
//输出边
for (int i = 0; i < g.n; ++i) {
printf("顶点%c:\n", g.V[i]);
for (int j = 0; j < g.n; ++j) {
if (g.E[i][j] != Maxint)
printf("边为<%c,%c>,权值为%d:\n", g.V[i], g.V[j], g.E[i][j]);
}
}
}
//找到顶点在顶点集中的标号
int LocateV(G_Amatreix g, VertexType v) {
int j = 0;
for (; j < g.n; ++j) {
if (g.V[j] == v)
return j;
}
return j;
}
int main(int argc, char* argv[]) {
G_Amatreix g;
CreateG(g);
return 0;
}

优缺点
优点
- 便于判断两顶点是否有边和添加边,根据邻接矩阵对应的值
- 便于统计顶点的度,根据邻接矩阵的对应的行或列
缺点
- 不便于顶点的添加删除,用的固定大小数组存储不便于添加删除。
- 不便于统计边的数目,需要扫描邻接表,O(n*n)
- 空间复杂度高。对于n个结点的邻接矩阵需要n*n个单元存储,即使是无向图可以用对称矩阵的压缩存储也需要n * (n+1) / 2的单元。空间复杂度都为 O ( n * n),对于稀疏矩阵来说,空间浪费严重
邻接表
存储思想
邻接表的实现是类似与树的孩子表示法的单链表和顺序存储结构结合的存储方式的。类似的把每一个顶点看作一个根结点,每一个与它有邻接关系的顶点都是它的孩子。为每个顶点创建一个头结点存储顶点信息和一个指针,指针指向一个与它有邻接关系的顶点结点。

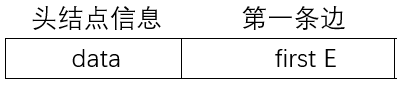
- 表头结点和边结点
若是表示网的话,可以在边结点中加入一个权值域来表示边的权值
- 邻接表和逆邻接表
无向图的邻接表可以通过每个顶点的边链表的结点数目知道顶点的度;而有向图边链表的结点数目仅表示出度,入度则需要遍历全表。所以为了便于计算顶点的入度,可以用图的逆邻接表(以弧的弧头为头结点,弧尾为边界点)来计算。
代码
邻接表ADT
///GAlist.h
#pragma once
#include<stdio.h>
#define MAX 20
//结点类型
typedef char VertexType;
typedef int Edgetype;
//边结点
typedef struct Enode{
int vnum;
Edgetype info;
struct Enode* Enext;
}ENode,*Ep;
//头结点
typedef struct Vnode{
VertexType v;
Ep fristE;
}VNode,Alist[MAX];
//邻接表
struct GAlist {
Alist list;
int n, e;
};
//创建图
void CreateG(GAlist& g);
//找到顶点在顶点集中的标号
int LocateV(GAlist g, VertexType v);
//释放边结点
void freeG(GAlist& g);
实现和测试
#include<stdio.h>
#include"GAlist.h"
/// ===============================================
/// 图接口实现
/// ===============================================
//创建图
void CreateG(GAlist& g) {
printf("input n , e:\n");
scanf_s("%d,%d", &g.n, &g.e);
getchar();
//初始化Alist
for (int i = 0; i < g.n; ++i) {
printf("input V[%d]:", i);
scanf_s("%c", &g.list[i].v, 1);
g.list[i].fristE = NULL;
char ch = getchar();
while (ch != '\n')
ch = getchar();
}
//输入边
char v1 = 0, v2 = 0;
int m = 0;
int j, k;
for (int i = 0; i < g.e; ++i) {
printf("input the edge:(v1 v2 w)\n");
scanf_s("%c %c %d", &v1, 1, &v2, 1, &m);
char ch = getchar();
while (ch != '\n')
ch = getchar();
j = LocateV(g, v1);
k = LocateV(g, v2);
//生成边结点
Ep p = new ENode;
p->vnum = k;
p->info = m;
p->Enext = g.list[j].fristE;
g.list[j].fristE = p;
//对称结点的边结点生成
Ep p2 = new ENode;
p2->vnum = j;
p2->info = m;
p2->Enext = g.list[k].fristE;
g.list[k].fristE = p2;
}
//输出
for (int i = 0; i < g.n; ++i) {
printf("顶点%c:\n", g.list[i].v);
Ep p = g.list[i].fristE;
if (!p)
printf("null");
while (p) {
int j;
Ep q = p->Enext;
j = p->vnum;
printf("边为<%c,%c>,权值为%d:\n", g.list[i].v, g.list[j].v, p->info);
p = q;
}
}
}
//找到顶点在顶点集中的标号
int LocateV(GAlist g, VertexType v) {
int j = 0;
for (; j < g.n; ++j) {
if (g.list[j].v == v)
return j;
}
return j;
}
//释放边结点
void freeG(GAlist& g) {
for (int i = 0; i < g.n; ++i) {
Ep p = g.list[i].fristE;
while (p) {
Ep q = p->Enext;
delete p;
p = q;
}
}
}
int main(int argc, char* argv[]) {
GAlist g;
CreateG(g);
freeG(g);
return 0;
}
测试结果

优缺点
优点:
- 链表便于结点的删除和增加结点。
- 统计边的数目,时间复杂度O(n+e)
- 空间效率高。空间复杂度为O(n+e),适用于稀疏图
缺点:- 对于一条边存在与否,需要遍历邻接表。
- 不便于计算顶点的度。无向图的边表结点数为度,但有向图的出度需要遍历邻接表。如果采用逆邻接表,结果相反。
十字链表(有向图改进版)
邻接链表的边结点注定存储后只能求得有向图的出度,而求入度还得遍历全邻接表,所以十字链表以弧结点存储,将相同的弧头和弧尾的结点链接起来,就只需要遍历该结点对于的边结点链就可以得到出度或入度。
存储思想
- 弧结点
- 头结点
书上一个例子:
代码
ADT头文件
///GClist.h 十字链表
#pragma once
#include<stdio.h>
#define MAX 20
typedef char VertexType;
typedef int Edgetype;
//弧结点
typedef struct Enode {
int Tnum;
int Hnum;
Edgetype info;
struct Enode* Tnext,* Hnext;
}ENode, * Ep;
//头结点
typedef struct Vnode {
VertexType v;
Ep Tfrist;
Ep Hfrist;
}VNode, Clist[MAX];
//十字链表
struct GClist {
Clist list;
int n, e;
};
//创建十字链表
void CreateG(GClist& g);
//找到顶点在顶点集中的标号
int LocateV(GClist g, VertexType v);
//释放边结点
void freeG(GClist& g);
实现和测试
#include<stdio.h>
#include"GClist.h"
/// ===============================================
/// 图接口实现
/// ===============================================
//创建图
void CreateG(GClist& g) {
printf("input n , e:\n");
scanf_s("%d,%d", &g.n, &g.e);
getchar();
//初始化Alist
for (int i = 0; i < g.n; ++i) {
printf("input V[%d]:", i);
scanf_s("%c", &g.list[i].v, 1);
g.list[i].Hfrist = NULL;
g.list[i].Tfrist = NULL;
char ch = getchar();
while (ch != '\n')
ch = getchar();
}
//输入边
char v1 = 0, v2 = 0;
int m = 0;
int j, k;
for (int i = 0; i < g.e; ++i) {
printf("input the edge:(v1 v2 w)\n");
scanf_s("%c %c %d", &v1, 1, &v2, 1, &m);
char ch = getchar();
while (ch != '\n')
ch = getchar();
j = LocateV(g, v1);
k = LocateV(g, v2);
//生成弧结点
Ep p = new ENode;
p->Tnum = j;
p->Hnum = k;
p->info = m;
//将弧结点放在弧尾的Tfirst指针后
p->Tnext = g.list[j].Tfrist;
g.list[j].Tfrist = p;
//将弧结点放在弧头的Hfirst指针后
p->Hnext = g.list[k].Hfrist;
g.list[k].Hfrist = p;
}
for (int i = 0; i < g.n; ++i) {
printf("顶点%c:\n", g.list[i].v);
Ep p = g.list[i].Tfrist;
Ep p1 = g.list[i].Hfrist;
//输出以顶点为弧尾的弧
printf("输出以%c为弧尾的弧\n", g.list[i].v);
while (p) {
Ep q = p->Tnext;
printf("边为<%c,%c>,权值为%d:\n", g.list[p->Tnum].v, g.list[p->Hnum].v, p->info);
p = q;
}
printf("输出以%c为弧头的弧\n", g.list[i].v);
while (p1) {
Ep q = p1->Hnext;
printf("边为<%c,%c>,权值为%d:\n", g.list[p1->Tnum].v, g.list[p1->Hnum].v, p1->info);
p1 = q;
}
}
}
//找到顶点在顶点集中的标号
int LocateV(GClist g, VertexType v) {
int j = 0;
for (; j < g.n; ++j) {
if (g.list[j].v == v)
return j;
}
return j;
}
//释放边结点
void freeG(GClist& g) {
for (int i = 0; i < g.n; ++i) {
Ep p = g.list[i].Hfrist;
while (p) {
Ep q = p->Hnext;
delete p;
p = q;
}
}
}
int main(int argc, char* argv[]) {
GClist g;
CreateG(g);
freeG(g);
return 0;
}
测试结果
将图中的v1-v4用a~d表示,测试结果
输出:
邻接多重表(无向图改进版)
无向图用邻接表表示的时候,同一条边会被存储为两个结点然后分别链接到两个顶点的链中,对于空间的浪费,使得我们用类似十字链表弧结点链接弧头弧尾的方式,将一个边的两个结点存储在一个边结点中,然后用两个结点的链接到这一个结点上。
存储思想
- 边结点
- 头结点
书上的例子
代码
ADT头文件
///GAMList.h 邻接多重表
#pragma once
#include<stdio.h>
#define MAX 20
typedef char VertexType;
typedef int Edgetype;
//边结点
typedef struct Enode {
int Lvertex;
int Rvertex;
Edgetype info;
struct Enode* Lnext, * Rnext;
}ENode, * Ep;
//头结点
typedef struct Vnode {
VertexType v;
Ep Efrist;
}VNode, AMlist[MAX];
//邻接多重链表
struct GAMlist {
AMlist list;
int n, e;
};
//创建十字链表
void CreateG(GAMlist& g);
//找到顶点在顶点集中的标号
int LocateV(GAMlist g, VertexType v);
//释放边结点
void freeG(GAMlist& g);
实现和测试
#include<stdio.h>
#include"GAMlist.h"
/// ===============================================
/// 图接口实现
/// ===============================================
//创建图
void CreateG(GAMlist& g) {
printf("input n , e:\n");
scanf_s("%d,%d", &g.n, &g.e);
getchar();
//初始化Alist
for (int i = 0; i < g.n; ++i) {
printf("input V[%d]:", i);
scanf_s("%c", &g.list[i].v, 1);
g.list[i].Efrist = NULL;
char ch = getchar();
while (ch != '\n')
ch = getchar();
}
//输入边
char v1 = 0, v2 = 0;
int m = 0;
int j, k;
for (int i = 0; i < g.e; ++i) {
printf("input the edge:(v1 v2 w)\n");
scanf_s("%c %c %d", &v1, 1, &v2, 1, &m);
char ch = getchar();
while (ch != '\n')
ch = getchar();
j = LocateV(g, v1);
k = LocateV(g, v2);
//生成边结点
Ep p = new ENode;
p->Lvertex = j;
p->Rvertex = k;
p->info = m;
//将边结点放在左顶点的Efirst指针后
p->Lnext = g.list[j].Efrist;
g.list[j].Efrist = p;
//将边结点放在右顶点的Efirst指针后
p->Rnext = g.list[k].Efrist;
g.list[k].Efrist = p;
}
for (int i = 0; i < g.n; ++i) {
printf("顶点%c:\n", g.list[i].v);
Ep p = g.list[i].Efrist;
Ep q = NULL;
printf("输出以%c为顶点的边\n", g.list[i].v);
while (p) {
if (i == p->Lvertex)
q = p->Lnext;
else
q = p->Rnext;
printf("边为<%c,%c>,权值为%d:\n", g.list[p->Lvertex].v, g.list[p->Rvertex].v, p->info);
p = q;
}
}
}
//找到顶点在顶点集中的标号
int LocateV(GAMlist g, VertexType v) {
int j = 0;
for (; j < g.n; ++j) {
if (g.list[j].v == v)
return j;
}
return j;
}
//释放边结点
void freeG(GAMlist& g) {
for (int i = 0; i < g.n; ++i) {
Ep p = g.list[i].Efrist;
Ep q=NULL;
while (p) {
if (i == p->Lvertex)
q = p->Lnext;
else
q = p->Rnext;
delete p;
p = q;
}
}
}
int main(int argc, char* argv[]) {
GAMlist g;
CreateG(g);
freeG(g);
return 0;
}
测试例子和结果