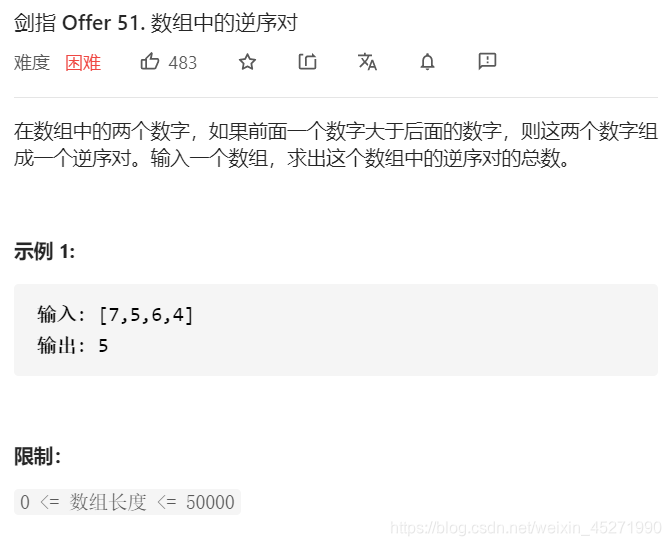
51.数组中的逆序对(※)
思路一:暴力
枚举每一个数字,然后遍历之后的数字,找到比当前数字小的
但是超时了
class Solution {
public int reversePairs(int[] nums) {
int res = 0;
for(int i = 0;i < nums.length;i++){
for(int j = i+1; j < nums.length;j++){
if(nums[i] > nums[j]){
res++;
}
}
}
return res;
}
}
思路二:归并排序
利用归并排序统计数组中的逆序对是非常常见的做法。
为什么归并排序可以做到统计数组的逆序对?
首先什么是归并排序?
归并排序涉及到两个阶段,一个是分 ,然后是和。
首先将数组一分为二,然后分别对左右的两个数组进行再次的递归处理,再次进行划分,直到每一个小区间的数组长度是1
那么每一个划分的小数组都可以看作是数组内有序的。
然后对相邻的左右两个数组进行合并
那么逆序对怎么算呢 ?
如果当前左边的元素大于当前右边的元素 ,那么右边元素可以对应的逆序对就是从左边元素到开始到左边数组结束。

==老是忘记数组的判定是否个数为0的情况 ==
以及拷贝数组的用法 (源数组(拷贝的数据从哪来),源数组下标, 目的数组(拷贝到那里去),拷贝数组下标,拷贝的长度)
class Solution {
int res = 0;
public int reversePairs(int[] nums) {
if(nums.length == 0) return res;
int length = nums.length;
int left = 0;
int right = length-1;
merSortInternal(nums,left,right);
return res;
}
private void merSortInternal(int[] nums, int left, int right) {
int length = right-left+1;
//说明划分区间已经结束了
//递归的终止条件
if(length == 1) return ;
int mid = (right + left)/2 ;
merSortInternal(nums,left,mid);
merSortInternal(nums,mid+1,right);
//开始对两个区间进行合并
merge(nums,left, mid, mid+1,right);
}
private void merge(int[] nums, int leftIndex, int mid , int rightIndex, int highIndex) {
int[] newArr = new int[highIndex-leftIndex+1];
int left = leftIndex;
int right = rightIndex;
int index = 0;
while (left <= mid && right <= highIndex){
while (left <= mid && right <= highIndex &&nums[left] <= nums[right]){
newArr[index++] = nums[left];
left++;
}
while (left <= mid && right <= highIndex && nums[left] > nums[right]){
newArr[index++] = nums[right];
//这里计算逆序对通过找到当前left 到mid 的个数
res += mid-left+1;
right++;
}
}
while (left <= mid){
newArr[index++] = nums[left];
left++;
}
while (right <= highIndex){
newArr[index++] = nums[right];
right ++;
}
//源数组 数组的来源 -- 目标数组 从哪开始拷贝的个数
System.arraycopy(newArr,0,nums,leftIndex,highIndex-leftIndex+1);
}
}
52. 两个链表的第一个公共结点(※※)
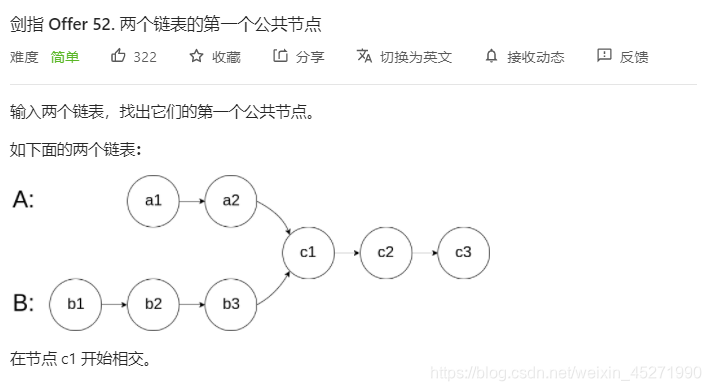
怎么说这个题呢,就是做一次,错一次,永远不可能一次做对,我不太懂我自己为啥会这样…
思路很多种 主要写一下双指针的思路。
定义两个指针,分别指向链表1和链表2 然后分别往后走
如果在这之中,出现某个指向为null 就让他指向另一个链表的头节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null || headB == null) return null;
ListNode cur1 = headA;
ListNode cur2 = headB;
while(cur1 != cur2){
if(cur1 == null) {
cur1 = headB;
}else{
cur1 = cur1.next;
}
if(cur2 == null){
cur2 = headA;
}else{
cur2 = cur2.next;
}
}
return cur1;
}
}
或者是用一个哈希表的做法
首先遍历链表headA,并将链表 headA 中的每个节点加入哈希集合中。
然后遍历链表headB,对于遍历到的每个节点,判断该节点是否在哈希集合中,即可。
53-I.在排序数组查找数字I

思路:二分查找
以nums[mid] < target 作为check函数
那么 左半部分是满足的 右半部分是不满足的,要找的是右半部分 第一个不满足的点 (二分的模板二) 所以更新mid的方式是(left+right)/2
class Solution {
public int search(int[] nums, int target) {
if(nums.length == 0) return 0;
int res = 0;
//二分查找
int left = 0;
int right = nums.length-1;
int mid = 0;
while(left < right){
mid = (left+right)/2;
if(nums[mid] < target){
left = mid+1;
}else {
right = mid;
}
}
//说明找到了
while(left < nums.length && nums[left] == target ){
res++;
left++;
}
return res;
}
}
53-II 0~n-1中缺失的数字

这个题的通俗意思就是下面这样的。

思路一:遍历比较
比较好写,注意 0 1 2 这种情况就可以了
class Solution {
public int missingNumber(int[] nums) {
for(int i = 0; i< nums.length;i++){
if(i != nums[i]) return i;
}
//最后就说明是少一个数字
return nums.length;
}
}
思路二:二分查找
排序数组的搜索问题,一定要先看看二分可不可以用
二分的check函数 是判断 当前的下标是否和数值相等 要找到第一个不相等的
如果相等left = mid+1
不相等 right = mid
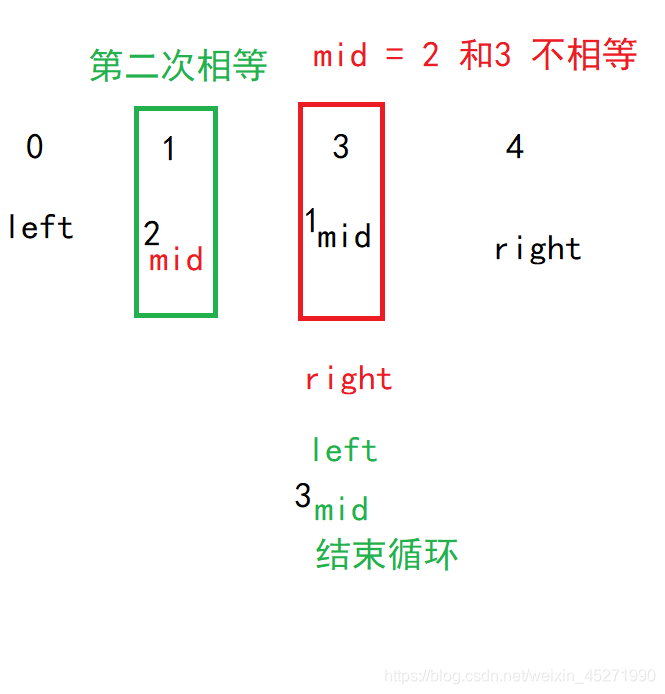
但是注意跳出的时候 因为是自己写死了二分查找的模板,所以最后有可能出现这样的情况

class Solution {
public int missingNumber(int[] nums) {
int bound = nums.length;
int left = 0;
int right = nums.length-1;
int mid = 0;
while(left < right){
mid = (left + right)/2;
if(nums[mid] == mid){
left= mid+1;
}else {
//如果发现了不匹配 应该接着往前找
right = mid;
}
}
if(left == nums[left]) return left+1;
return left;
}
}
发现自己两个53的二分查找搜写的不顺畅,果然啊学过的东西不复习,就算简单也有可能会忘掉的。
还是遍历最简单,暴力永远是一切算法的的神啊。
54.二叉搜索树的第k大节点
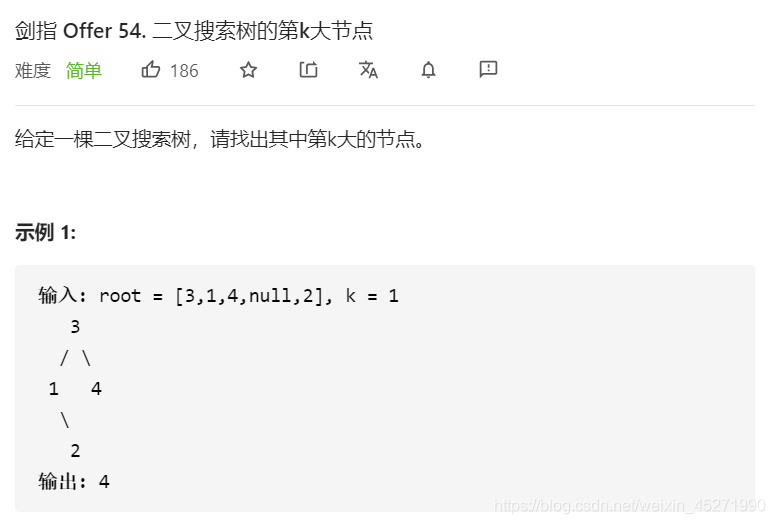
1 ≤ k ≤ 二叉搜索树元素个数
中序遍历的结果是有序的 依次递增 左根右
那么颠倒中序遍历的顺序 右根左 即可得到倒叙序列 同时得到第k个即可。
用一个全局变量来维护当前遍历到的第几大
class Solution {
int count;
int number;
public int kthLargest(TreeNode root, int k) {
count = k;
dfs(root);
return number;
}
public void dfs(TreeNode root){
if(root == null) return ;
//右
dfs(root.right);
//根
if(count-1 == 0) {//如果当前是第k个那么 number 赋值,count一定要变化 然后往回递归
number = root.val;
count--; //这里必须要变化,否则往会递归层层跳出的时候 number会重复赋值
return;
}else{ // 如果当前的root 不是那么就一直遍历就好啦。
count--;
}
//左
dfs(root.left);
}
}
55-II.平衡二叉树 (※※)
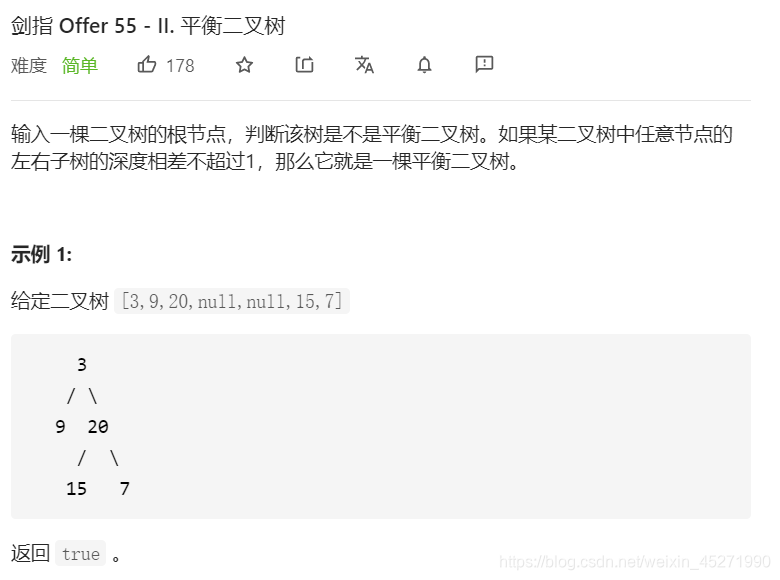
采用自底向上的做法
层层向上汇报 如果当前的左子树的高度是-1 或者右子树的高度是-1 或者两棵树的高度差是-1 那么就要返回-1。
是一道easy,但老写错…
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null || root.left == null && root.right == null) return true;
return dfs(root) != -1;
}
public static int dfs(TreeNode root){
if(root == null) return 0;
int leftHigh = dfs(root.left);
int rightHigh = dfs(root.right);
if(leftHigh == -1 || rightHigh == -1 || Math.abs(leftHigh-rightHigh) >1){
return -1;
}else {
return Math.max(leftHigh,rightHigh)+1;
}
}
}
56-I.数组中数字出现的次数 (√)

思路一:对数组排序,然后两两进行比较
如果当前的和后一个不相等那么当然加入结果集
如果当前的和后一个相等 那么手动让i+1 之后循环的i++就可以跳过这对相等的。
但是注意一个判断的条件 当i = = length-1 的时候循环时无法进去的,那么如果最后一个和之前的相等
此时的i = = length 如果和最后一个不相等,就需要加入结果,所以最后需要特判一下。
class Solution {
public int[] singleNumbers(int[] nums) {
Arrays.sort(nums);
int[] res = new int[2];
int index = 0;
int i = 0;
for(i =0; i < nums.length-1;i++){
if(nums[i] != nums[i+1]){
res[index++] = nums[i];
}else{
i = i+1;
}
}
if(i == nums.length-1) res[1] = nums[i];
return res;
}
}
思路二:位运算
首先将数组的所有元素整体异或运算一遍,得到结果 temp 就是两个不相同的数字异或的结果。
之后对这个temp进行位运算,找到第一个二进制为1 的比特位,然后根据第一个二进制为1的比特位就可以得到一个split数字,把整个数组按照这个split 一分为二。
如何做到呢?
- 首先两个不同的数字某个比特位的异或的结果是1,那么就说明他们两个的这一位是不一样的。
- 那么就让split 和所有数字按位与一次 这两个数字按位与的结果肯定不一样就被分到了两个组
- 其他数字也是不用管 数字被分到了那一组 可以肯定的是 每一组里面除了一个不同的额数字 其他都是出现了两次就可以
- 结果是0 分到一个组
- 不是0的分到一个组 (注意一定写的是不是0 而不是写==1 )
class Solution {
public int[] singleNumbers(int[] nums) {
//全部异或一遍 得到是两个出现一次的数字的异或结果
int temp = 0;
for(int num: nums){
temp ^= num;
}
//遍历这个异或的结果 看看哪一个位置是1 然后得到这个对应的十进制数字就可以把数组一分为二
int count = 0;
while(count < 32){
if(( (temp >> count )& 1 )== 1){
break;
}
count++;
}
//跳出循环后找到了第一个1的二进制位
int[] res = new int[2];
int split = Math.pow(2,count);
for(int num:nums){
if((num & split) == 0) {
res[0] ^= num;
}else{
res[1] ^= num;
}
}
return res;
}
}
56-II.数组中出现的次数II (√)

思路一:排序+二分查找的变形
如果最后没有返回 结束了循环
那么最后一个数字就是要找的数字
比如 333 4
class Solution {
public int singleNumber(int[] nums) {
Arrays.sort(nums);
int left = 0;
int right = 1;
while(left < right && right < nums.length){
if(nums[left] != nums[right]){
return nums[left];
}
while(left < right && nums[left] == nums[right]){
right++;
}
left = right;
right = left+1;
}
return nums[left];
}
}
思路二:位运算
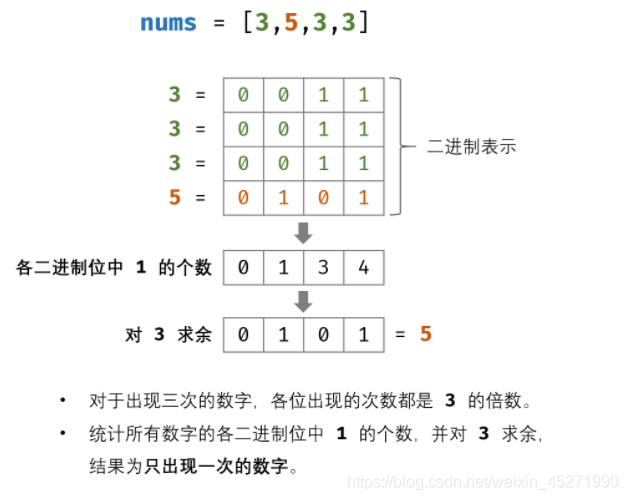
这种思想确实是想不到的,但是见过一次,有个印象开阔思路吧。
对应的一种解法是使用一个32位的哈希表,但是空间复杂度太大。但是那个有限状态机的解法我也确实看不懂,主要是真的看不进去… 所以我觉得思路一就是一个不错的解法!
class Solution {
public int singleNumber(int[] nums) {
int[] count = new int[32];
for(int num: nums){
//遍历一个数字的32位
for(int j = 0; j<32;j++){
count[j]+= (num >> j) & 1;
}
}
//然后每一位 % 3 同时进行运算
int res = 0;
for (int i= 0;i<32;i++){
count[i] = count[i] %3;
if (count[i] == 1) {
res += Math.pow(2,i);
}
}
return res;
}
}
57.和为s的两个数字 (※)

思路一:朴素哈希法
class Solution {
public int[] twoSum(int[] nums, int target) {
HashSet<Integer> set = new HashSet<>();
for(int num : nums){
if(set.contains(target - num)){
return new int[]{target-num,num};
}else{
set.add(num);
}
}
return new int[2];
}
}
思路二:二分查找+双指针
哈希表的空间复杂度O(n)
二分查找首先找到最后一个比target小的数字,然后利用双指针找到和为target的两个数字。
class Solution {
public int[] twoSum(int[] nums, int target) {
int leftIndex = 0;
int rightIndex = binarySearch(nums,target);
while (leftIndex < rightIndex){
if(nums[leftIndex] + nums[rightIndex] == target){
return new int[]{nums[leftIndex],nums[rightIndex]};
}
if(nums[leftIndex] + nums[rightIndex] < target){
leftIndex++;
}else {
rightIndex--;
}
}
return new int[2];
}
private int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
int mid = 0;
while (left < right){
mid = (left + right+1)/2;
if(nums[mid] < target){
left =mid;
}else {
right = mid-1;
}
}
return left;
}
}
57-II.和为s的连续正数序列 (※)
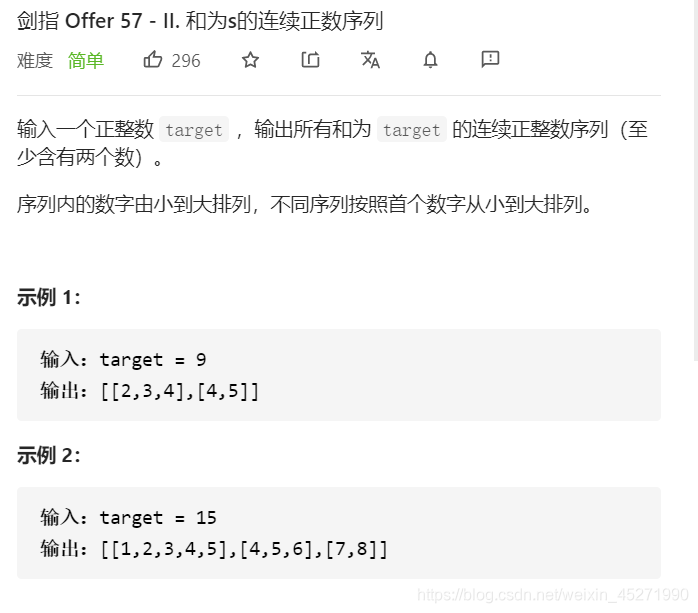
思路一:滑动窗口
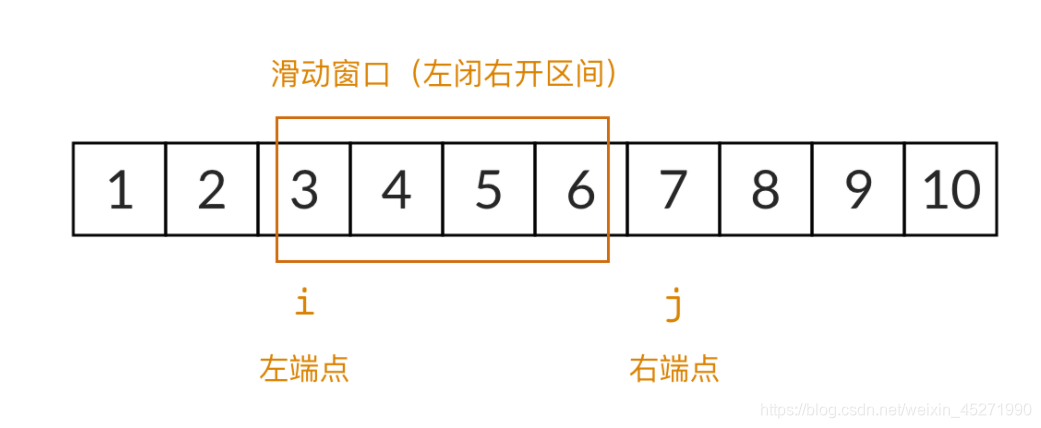
注意滑动窗口都是只可以向右滑动
滑动停止搜索的条件 一定是左窗口的值 <= target的一半!
class Solution {
public int[][] findContinuousSequence(int target) {
int left = 1;
int right = 1;
int sum = 0;
List<int[]> res = new ArrayList<>();
//结束查找的条件 如果滑动窗口最左边的数字 都要比target还要大的话
//进一步优化条件 因为是一个有序递增不重复的序列 所以如果 最左边的数字 比target的一半还要大 那么就结束
//一定要写 <= target = 5 5/2 = 2
while (left <= target/2){
if(sum < target){
sum+= right;
right++;
}else if(sum > target){
sum -= left;
left++;
}else {
//记录结果
int[] arr = new int[right-left];
for(int k = left;k < right;k++){
arr[k-left] = k;
}
res.add(arr);
//然后继续去找下一个结果
sum -=left;
left++;
}
}
return res.toArray(new int[res.size()][]);
}
}
然后是关于这句话
res 这个数组链表里面存放的是数组 转换为二维数组这样写!要指明第一维度的长度
return res.toArray(new int[res.size()][]);
愚蠢的我,其实最先想到的办法是暴力枚举,甚至还想用深搜+记忆数组的优化去写…
59 - I. 滑动窗口的最大值 (※)
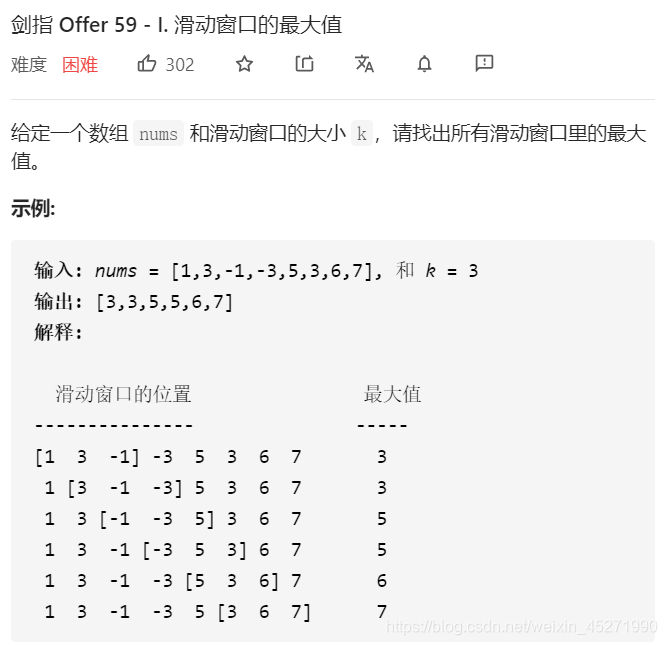
思路一:暴力法
找到窗口的范围区间,然后每一次再范围区间内找到最大值的时间复杂度是o(k)
数组长度的是n窗口大小是k 可以形成的窗口数 (n-k+1)个窗口;
关于计算窗口数量

思路二: 构造一个单调队列
使得找最大值的时间复杂度降低到o(1)
每次进入队列的时候 弹出所有比当前进入队列都小的值 维护的队列是一个非单调递增( 也就是说可能单调递减,也可能是相邻的值相等的情况)

除了维护好一个单调的队列以外,还有一个坑就是当right = num.lenght-1 也就是最后一个元素的时候,循环不可以再进去了。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0) return new int[0];
int left = 0;
int right = k-1;
int[] res = new int[nums.length-k+1];
Deque<Integer> queue = new LinkedList<>();
int index = 0;
//窗口初始化
for(int i =0;i < k;i++){
if(!queue.isEmpty()){
while (!queue.isEmpty() && nums[i] >queue.peekLast()){
queue.removeLast();
}
}
queue.addLast(nums[i]);
}
res[index++] = queue.peekFirst();
//移动窗口
//坑!
while (right < nums.length-1){
if(!queue.isEmpty() && nums[left] == queue.peekFirst()){
queue.removeFirst();
}
left++;
right++;
while (!queue.isEmpty() && nums[right] > queue.peekLast()){
queue.removeLast();
}
queue.addLast(nums[right]);
res[index++] = queue.peekFirst();
}
return res;
}
}
59.-II 队列的最大值 (※)
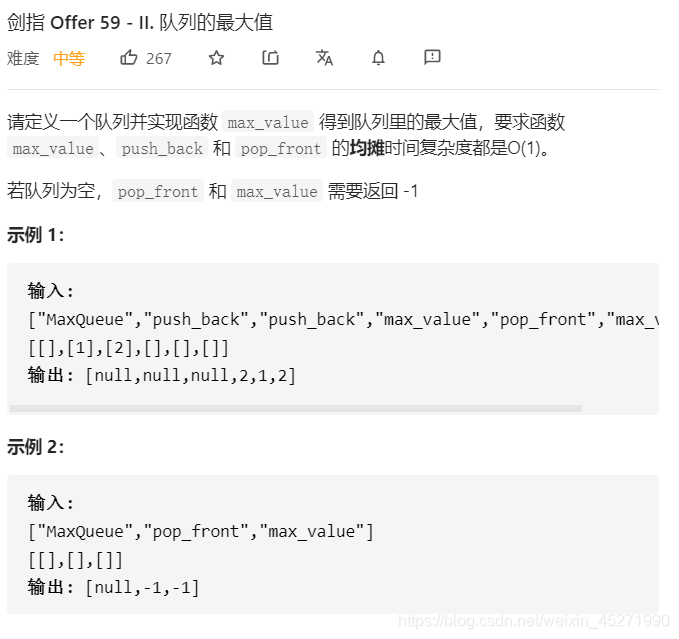
为了实现此递减列表,需要使用 双向队列 ,假设队列已经有若干元素:
当执行入队 push_back() 时: 若入队一个比队列某些元素更大的数字 xx ,则为了保持此列表递减,需要将双向队列 尾部所有小于 xx 的元素 弹出。
当执行出队 pop_front() 时: 若出队的元素是最大元素,则 双向队列 需要同时 将首元素出队 ,以保持队列和双向队列的元素一致性。
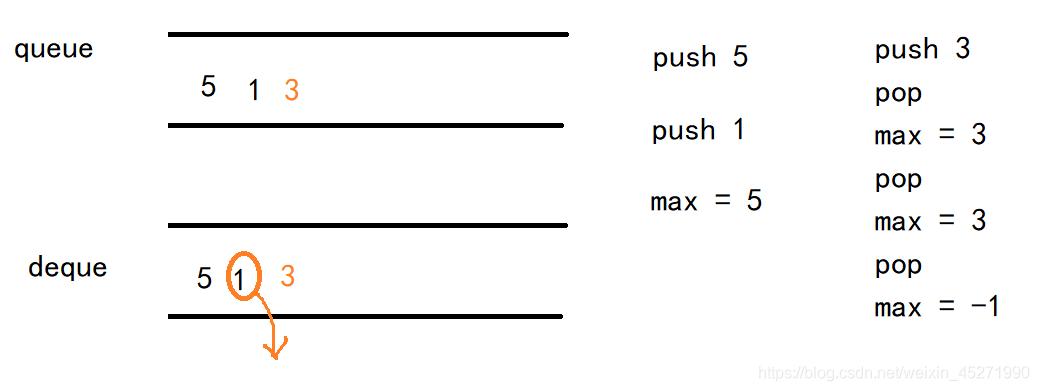
class MaxQueue {
/**
* 维护一个单调不递增的序列
* 也就是说这个双端队列中的样子是
* 5 4 3 2
* 5 5 4 4 2 2
*/
Queue<Integer> queue = null;
Deque<Integer> temp = null;
public MaxQueue() {
queue = new LinkedList<>();
temp = new LinkedList<>();
}
public int max_value() {
if(temp.size() == 0){
return -1;
}
//否则返回队尾元素
return temp.peekFirst();
}
public void push_back(int value) {
queue.add(value);
while (temp.size() != 0 && value > temp.peekLast()){
temp.removeLast();
}
temp.addLast(value);
}
public int pop_front() {
if(queue.size() != 0){
int num = queue.remove();
if(temp.size()!= 0 &&num == temp.peekFirst()){
temp.remove();
}
return num;
}
return -1;
}
}
60.n个骰子的点数(※)
这个动态规划,蛮有意思的,可以多看看。
/**
* 普通的动态规划
* double 是用来存放所有可能的点数和 那么double 的取值范围 [n*1,n*6]
* 1 <=i <= n
* n*1 <=j <= n*6
* dp [i][j] 表示的是 用了i个骰子 可以得到的点数和的概率
*
* 状态转移方程
* 也就是说当前的状态 可能是在上一个骰子基础上 新增加的骰子点数是 k = 1 2 3 4 5 6
* dp[i][j] = dp[i-1][j-1]/6 + dp[i-1][j-2]/6 + ...+ dp[i-1][j-6]/6
* 但是注意处理可能的越界问题
* 必须要保证 j-k >0
* dp[2][2] = dp[1][2-1]
* 同时 j >= i
* @param n
* @return
*/
class Solution {
public double[] dicesProbability(int n) {
double[] res = new double[5*n+1];//为了方便理解 从点数和也就是下标1 表示1 开始
double dp[][] = new double[n+1][n*6+1];
//初始化
for(int i = 1;i <= 6;i++){
dp[1][i] = 1.0/6; //注意这里用小数点计算嗷!
}
//枚举每一个骰子可以形成的点数
for(int i = 2; i <= n;i++){
for(int j = i; j <= i*6;j++){ // 2个骰子最小的点数和是2
//为什么这里不可以用 k <= j 因为j 是可以取7 的但是骰子的最大数值是6
for(int k= 1;k<=6;k++){
if(j-k >0) {
dp[i][j] += dp[i - 1][j - k] / 6; //表示之前的i-1个骰子和是j-k 的概率 + 第i个骰子的是j的概率
}else {
break;
}
}
}
}
//遍历所有的集合
//res结果的数量就是 n个骰子的取值范围 的差
// 6*n -n = 5n;
for(int i = 0; i <= 5*n;i++){
res[i] = dp[n][n+i];
}
//就是吧所有的dp[n] 的元素搬出来就好啦
//其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
return res;
}
}
可能要做的事情太多了吧,但是一件件的来吧,感觉老是看着哪些要做却没做的很多东西会很焦虑的。
分享一句话给自己加个油。希望你自大,眼里永远闪着不妥协的光!