链表–常见应用场景
链表反转
单向表的反转,是面试中的一个高频题目。
需求:
单向链表
- 原链表中数据为:1->2->3>4
- 反转后链表中数据为:4->3->2->1
反转API:

原来解析:
- 使用递归可以完成反转,递归反转其实就是从原链表的第一个存数据的结点开始,依次递归调用反转每一个结点,直到把最后一个结点反转完毕,整个链表就反转完毕。
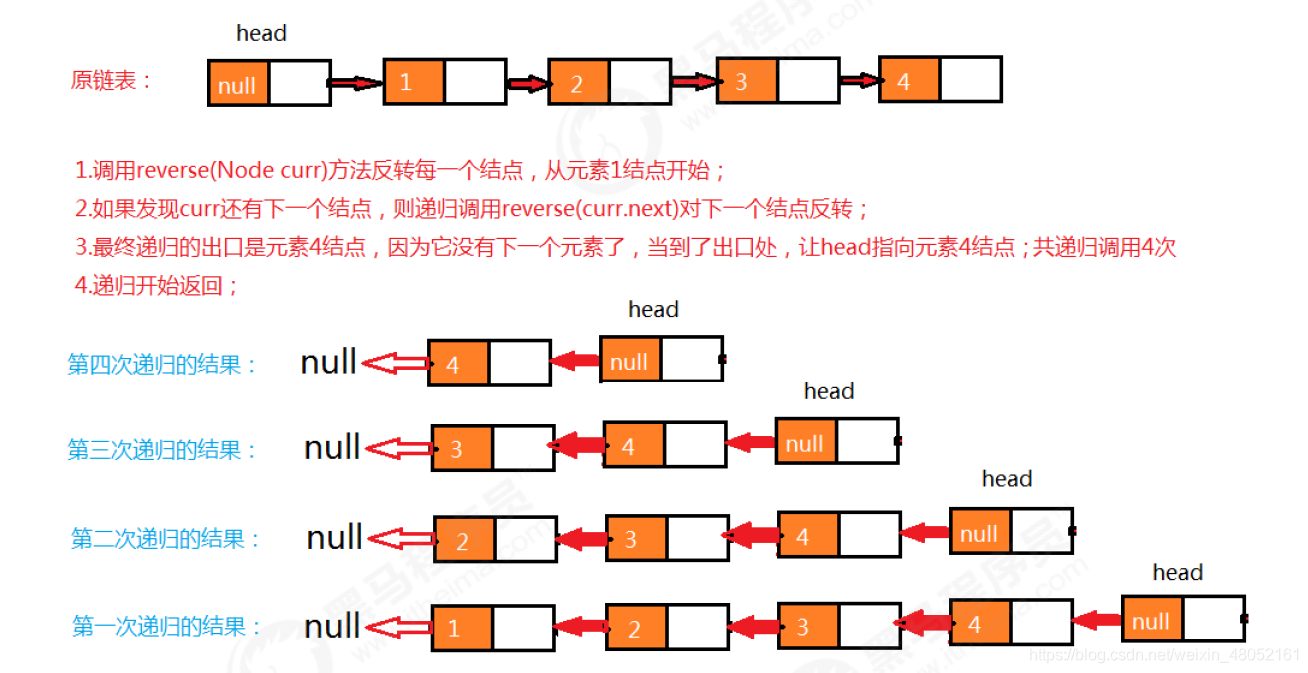
代码实现:
- 单向链表LinkList
//用来反转整个链表
public void reverse(){
//判断当前链表是否为空链表,如果是空链表,则结束运行,如果不是,则调用重载的reverse方法完成反转
if (isEmpty()){
return;
}
reverse(head.next);
}
//反转指定的结点curr,并把反转后的结点返回
public Node reverse(Node curr){
if (curr.next==null){
head.next=curr;
return curr;
}
//递归的反转当前结点curr的下一个结点;返回值就是链表反转后,当前结点的上一个结点
Node pre = reverse(curr.next);
//让返回的结点的下一个结点变为当前结点curr;
pre.next=curr;
//把当前结点的下一个结点变为null
curr.next=null;
return curr;
}
测试:
@Test
public void test01(){
LinkList<Integer> list = new LinkList<>();
list.insert(1);
list.insert(2);
list.insert(3);
list.insert(4);
for (Integer i : list) {
System.out.print(i+" ");
}
System.out.println();
System.out.println("--------------------");
list.reverse();
for (Integer i : list) {
System.out.print(i+" ");
}
}
快慢指针
- 快慢指针指的是定义两个指针,这两个指针的移动速度一块一慢,以此来制造出自己想要的差值,这个差值可以然我们找到链表上相应的结点。一般情况下,快指针的移动步长为慢指针的两倍
1. 中间值问题
需求;
- 找到一串节点当中的中间值元素
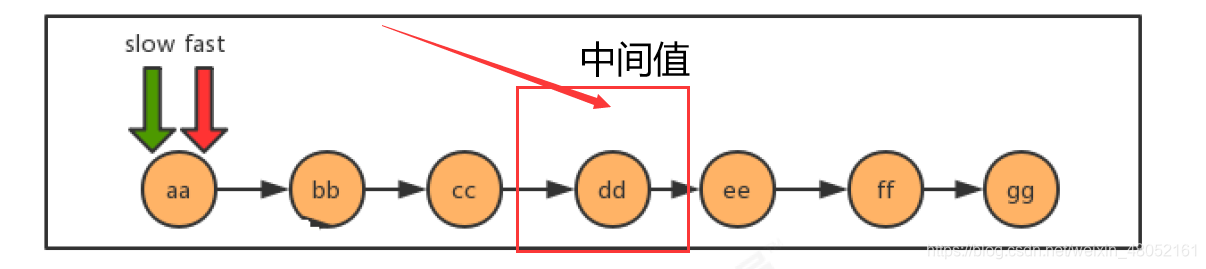
原理分析:
- 利用快慢指针,我们把一个链表看成一个跑道,假设a的速度是b的两倍,那么当a跑完全程后,b刚好跑一半,以此来达到找到中间节点的目的。
图解:
- 如下图,最开始,slow与fast指针都指向链表第一个节点,然后slow每次移动一个指针,fast每次移动两个指针。
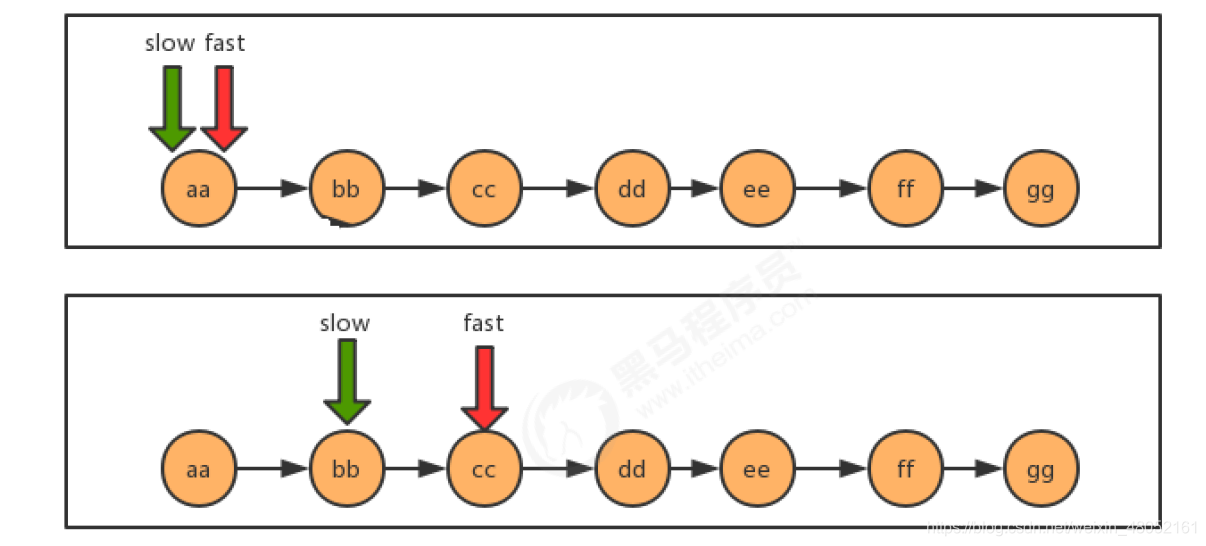
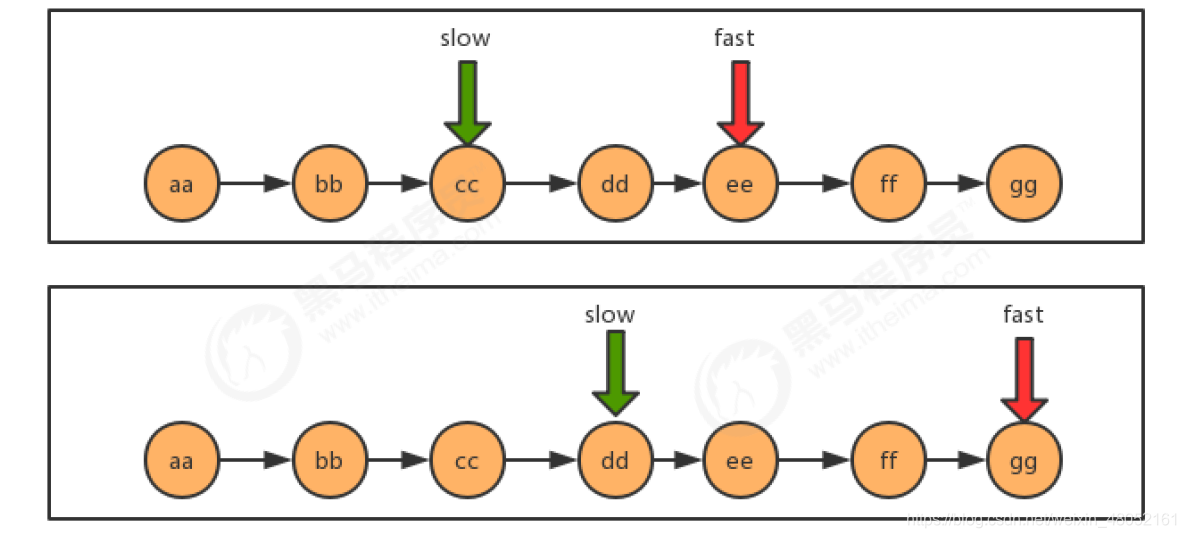
代码:
/**
* @param first 链表的首结点
* @return 链表的中间结点的值
*/
public static String getMid(Node<String> first) {
//定义两个指针
Node<String> fast = first;
Node<String> slow = first;
//使用两个指针遍历链表,当快指针指向的结点没有下一个结点了,就可以结束了,结束之后,慢指针指向的结点就是中间值
while(fast!=null &&fast.next!=null){
//变化fast的值和slow的值
fast = fast.next.next;
slow=slow.next;
}
return slow.item;
}
测试:
public class FastSlowTest {
public static void main(String[] args) throws Exception {
//创建结点
Node<String> first = new Node<String>("aa", null);
Node<String> second = new Node<String>("bb", null);
Node<String> third = new Node<String>("cc", null);
Node<String> fourth = new Node<String>("dd", null);
Node<String> fifth = new Node<String>("ee", null);
Node<String> six = new Node<String>("ff", null);
Node<String> seven = new Node<String>("gg", null);
//完成结点之间的指向
first.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
fifth.next = six;
six.next = seven;
//查找中间值
String mid = getMid(first);
System.out.println("中间值为:"+mid);
}
/**
* @param first 链表的首结点
* @return 链表的中间结点的值
*/
public static String getMid(Node<String> first) {
//定义两个指针
Node<String> fast = first;
Node<String> slow = first;
//使用两个指针遍历链表,当快指针指向的结点没有下一个结点了,就可以结束了,结束之后,慢指针指向的结点就是中间值
while(fast!=null &&fast.next!=null){
//变化fast的值和slow的值
fast = fast.next.next;
slow=slow.next;
}
return slow.item;
}
//结点类
private static class Node<T> {
//存储数据
T item;
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
2. 单向链表是否有环问题
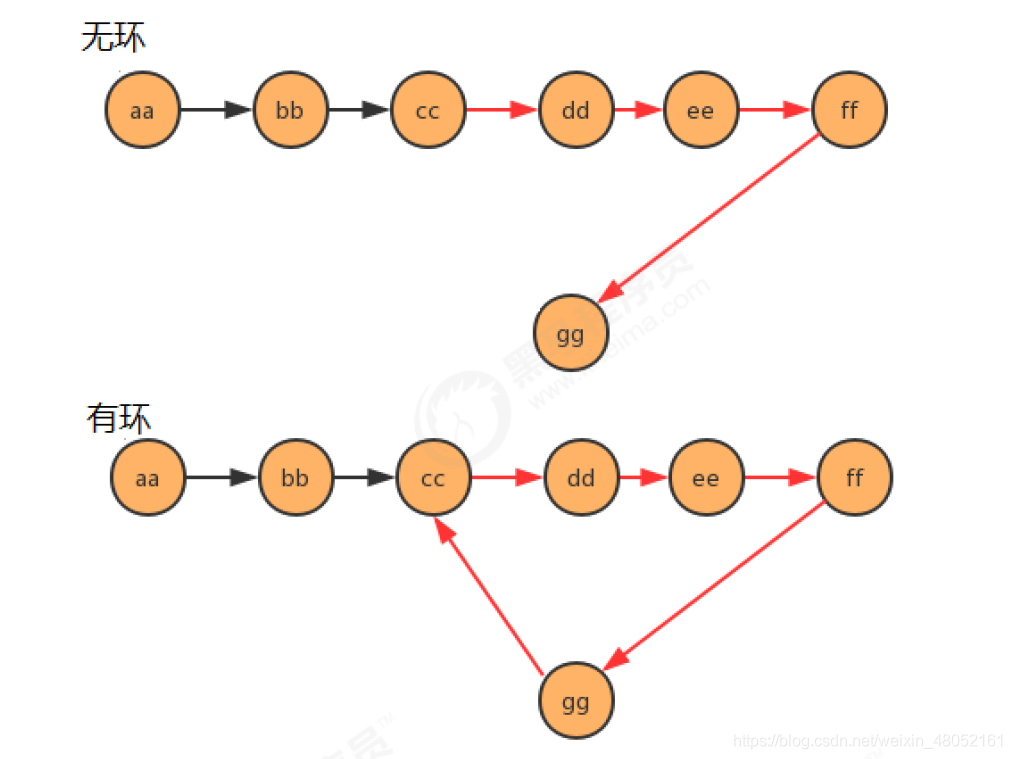
原理解析:
- 使用快慢指针的思想,还是把链表比作一条跑道,链表中有环,那么这条跑道就是一条圆环跑道,在一条圆环跑道中,两个人有速度差,那么迟早两个人会相遇,只要相遇那么就说明有环。
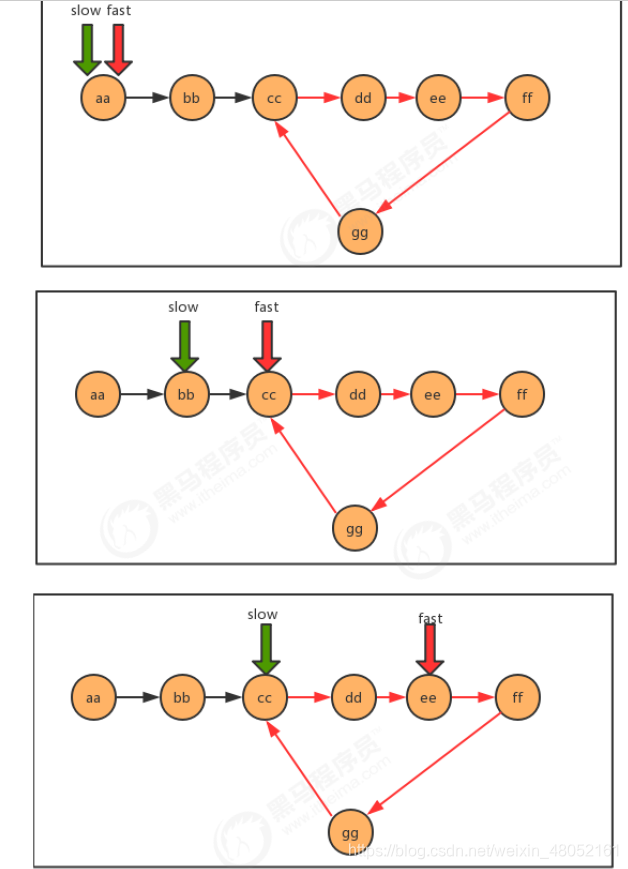
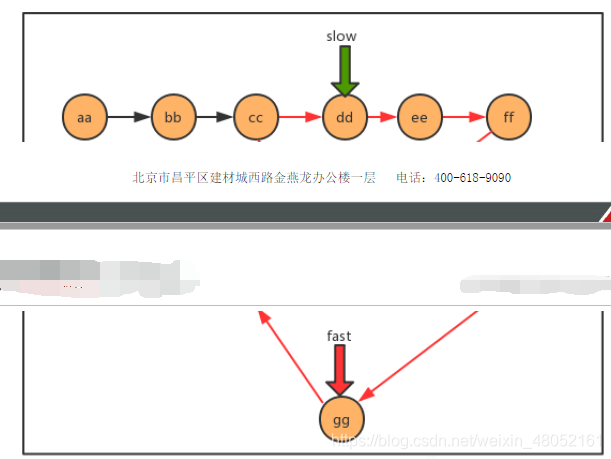
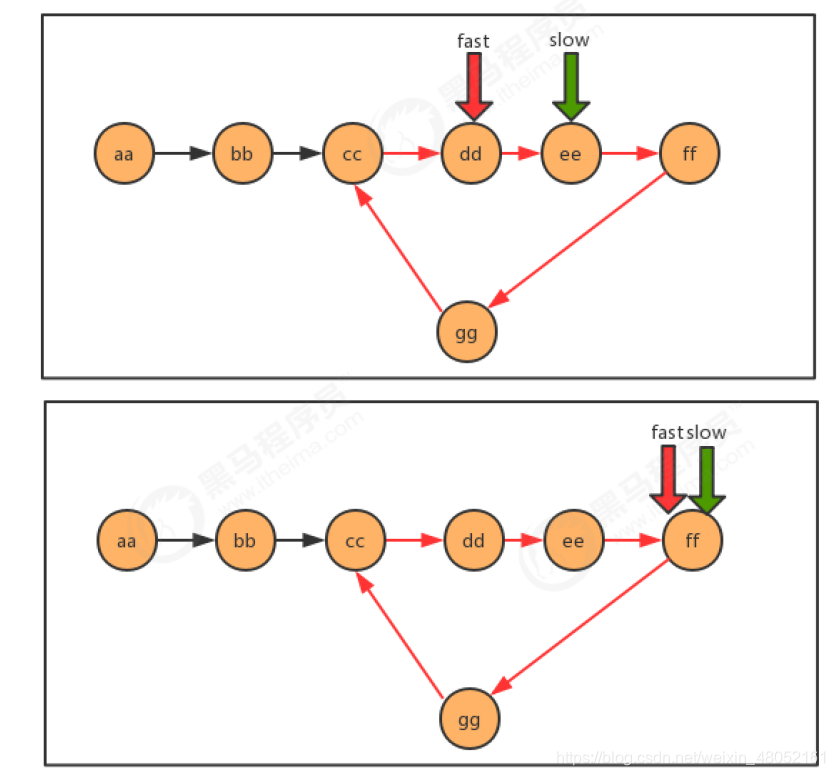
代码
/**
* 判断链表中是否有环
* @param first 链表首结点
* @return ture为有环,false为无环
*/
public static boolean isCircle(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
//遍历链表,如果快慢指针指向了同一个结点,那么证明有环
while(fast!=null && fast.next!=null){
//变换fast和slow
fast = fast.next.next;
slow = slow.next;
if (fast.equals(slow)){
return true;
}
}
return false;
}
测试
public class CircleListCheckTest {
public static void main(String[] args) throws Exception {
//创建结点
Node<String> first = new Node<String>("aa", null);
Node<String> second = new Node<String>("bb", null);
Node<String> third = new Node<String>("cc", null);
Node<String> fourth = new Node<String>("dd", null);
Node<String> fifth = new Node<String>("ee", null);
Node<String> six = new Node<String>("ff", null);
Node<String> seven = new Node<String>("gg", null);
//完成结点之间的指向
first.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
fifth.next = six;
six.next = seven;
// //产生环
seven.next = third;
//判断链表是否有环
boolean circle = isCircle(first);
System.out.println("first链表中是否有环:"+circle);
}
/**
* 判断链表中是否有环
* @param first 链表首结点
* @return ture为有环,false为无环
*/
public static boolean isCircle(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
//遍历链表,如果快慢指针指向了同一个结点,那么证明有环
while(fast!=null && fast.next!=null){
//变换fast和slow
fast = fast.next.next;
slow = slow.next;
if (fast.equals(slow)){
return true;
}
}
return false;
}
//结点类
private static class Node<T> {
//存储数据
T item;
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
3. 有环链表入口问题:
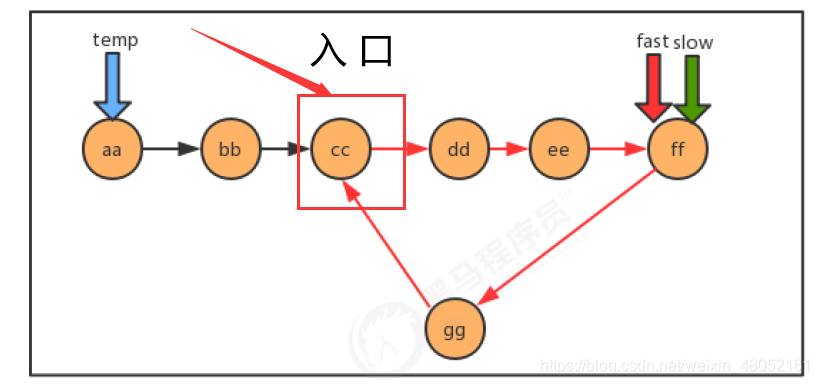
原理解析:
- 当快慢指针相遇时,我们可以判断到链表中有环,这时重新设定一个新指针指向链表的起点,且步长与慢指针一样为1,则慢指针与“新”指针相遇的地方就是环的入口。证明这一结论牵涉到数论的知识,这里略,只讲实现。
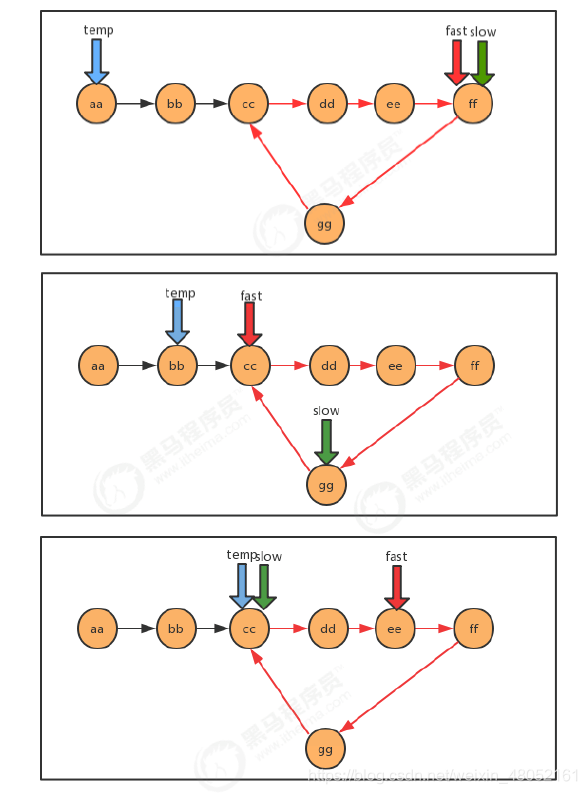
代码:
/**
* 查找有环链表中环的入口结点
* @param first 链表首结点
* @return 环的入口结点
*/
public static Node getEntrance(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
Node<String> temp = null;
//遍历链表,先找到环(快慢指针相遇),准备一个临时指针,指向链表的首结点,继续遍历,直到慢指针和临时指针相遇,那么相遇时所指向的结点就是环的入口
while(fast!=null && fast.next!=null){
//变换快慢指针
fast = fast.next.next;
slow = slow.next;
//判断快慢指针是否相遇
if (fast.equals(slow)){
temp = first;
continue;
}
//让临时结点变换
if (temp!=null){
temp = temp.next;
//判断临时指针是否和慢指针相遇
if (temp.equals(slow)){
break;
}
}
}
return temp;
测试:
package main.java.Algorithms.linear;
public class CircleListInTest {
public static void main(String[] args) throws Exception {
Node<String> first = new Node<String>("aa", null);
Node<String> second = new Node<String>("bb", null);
Node<String> third = new Node<String>("cc", null);
Node<String> fourth = new Node<String>("dd", null);
Node<String> fifth = new Node<String>("ee", null);
Node<String> six = new Node<String>("ff", null);
Node<String> seven = new Node<String>("gg", null);
//完成结点之间的指向
first.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
fifth.next = six;
six.next = seven;
//产生环
seven.next = third;
//查找环的入口结点
Node<String> entrance = getEntrance(first);
System.out.println("first链表中环的入口结点元素为:"+entrance.item);
}
/**
* 查找有环链表中环的入口结点
* @param first 链表首结点
* @return 环的入口结点
*/
public static Node getEntrance(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
Node<String> temp = null;
//遍历链表,先找到环(快慢指针相遇),准备一个临时指针,指向链表的首结点,继续遍历,直到慢指针和临时指针相遇,那么相遇时所指向的结点就是环的入口
while(fast!=null && fast.next!=null){
//变换快慢指针
fast = fast.next.next;
slow = slow.next;
//判断快慢指针是否相遇
if (fast.equals(slow)){
temp = first;
continue;
}
//让临时结点变换
if (temp!=null){
temp = temp.next;
//判断临时指针是否和慢指针相遇
if (temp.equals(slow)){
break;
}
}
}
return temp;
}
//结点类
private static class Node<T> {
//存储数据
T item;
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
约瑟夫问题
问题描述:

问题转换:
首先41个人坐一圈,第一个人编号为1,第二个人编号为2,第n个人编号为n。
- 编号为1的人开始从1报数,依次向后,报数为3的那个人退出圈;
- 自退出那个人开始的下一个人再次从1开始报数,以此类推;
- 求出最后退出的那个人的编号。
图示:
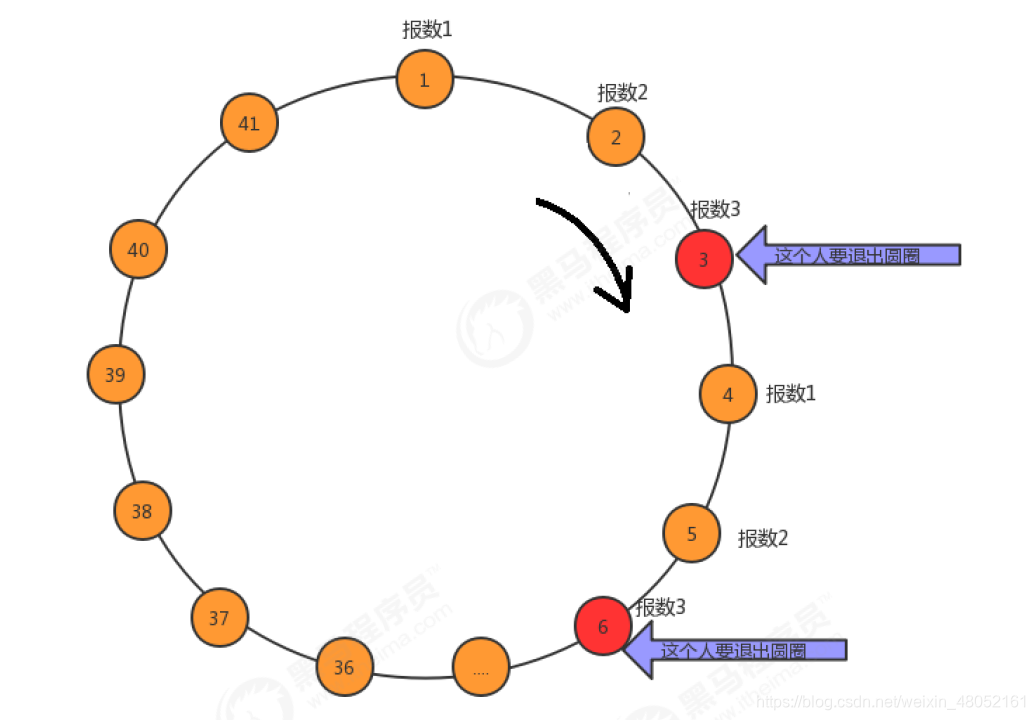
解题思路:
- 构建含有41个结点的单向循环链表,分别存储1~41的值,分别代表这41个人;
- 使用计数器count,记录当前报数的值;
- 遍历链表,每循环一次,count++;
- 判断count的值,如果是3,则从链表中删除这个结点并打印结点的值,把count重置为0;
代码:
善于创建临时变量指针来记录关键元素
package main.java.Algorithms.linear;
import org.jetbrains.annotations.NotNull;
/**
* 解决约瑟夫问题
*/
public class JosephTest01 {
public static void main(String[] args) {
//1.构建循环链表,包含41个结点,分别存储1~41之间的值
Node<Integer> first = getNodeList();
//2.遍历循环链表,找出报数为3的节点,并打印出来
run(first);
}
/**
* 构建循环链表,包含41个结点,分别存储1~41之间的值
* @return 返回链表存储的第一个元素
*/
private static Node<Integer> getNodeList() {
//用来就首结点
Node<Integer> first = null;
//用来记录前一个结点
Node<Integer> pre = null;
for (int i = 1; i <= 41; i++) {
//如果是第一个结点
if (i == 1) {
first = new Node<>(i, null);
pre = first;
continue;
}
//如果不是第一个结点
Node<Integer> newNode = new Node<>(i, null);
pre.next = newNode;
pre = newNode;
//如果是最后一个结点,那么需要让最后一个结点的下一个结点变为first,变为循环链表了
if (i == 41) {
pre.next = first;
}
}
return first;
}
/**
* 遍历循环链表,找出报数为3的节点,并打印出来
*/
private static void run(Node<Integer> first) {
//1.需要count计数器,模拟报数
int count = 0;
//2.遍历循环链表
//记录每次遍历拿到的结点,默认从首结点开始
Node<Integer> n = first;
//记录当前结点的上一个结点
Node<Integer> before = null;
while (n != n.next) {
//模拟报数
count++;
//判断当前报数是不是为3
if (count == 3) {
//如果是3,则把当前结点删除调用,打印当前结点,重置count=0,让当前结点n后移
before.next = n.next;
System.out.print(n.item + ",");
count = 0;
n = n.next;
} else {
//如果不是3,让before变为当前结点,让当前结点后移;
before = n;
n = n.next;
}
}
//打印最后一个元素
System.out.println(n.item);
}
/**
* 结点类
*/
private static class Node<T> {
//存储数据
T item;
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
