21.?栈的压入、弹出序列
描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
分析
使用辅助栈模拟弹出过程,最后辅助栈为空则表示参数中的弹出顺序可以实现。
import java.util.ArrayList;
import java.util.Stack;
public class Solution {
public boolean IsPopOrder(int [] pushA,int [] popA) {
Stack<Integer> stack = new Stack<>();
int index = 0;
for (int i : popA)
{
while(true)
{
if(!stack.isEmpty() && stack.lastElement().equals(i))
{
stack.pop();
break;
}
else
{
if (index < pushA.length)
{
stack.push(pushA[index]);
index++;
}
else
{
break;
}
}
}
}
if (stack.isEmpty())
return true;
else
return false;
}
}22.?从上往下打印二叉树
描述
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
分析
借助队列的特点(先进先出),使用循环,不断将加入队列的元素添加到列表。
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> list = new ArrayList<Integer>();
Queue<TreeNode> queue = new LinkedList<TreeNode>();
if (root == null)
return list;
queue.offer(root);
while(!queue.isEmpty())
{
TreeNode temp = queue.poll();
if (temp.left != null)
queue.offer(temp.left);
if (temp.right != null)
queue.offer(temp.right);
list.add(temp.val);
}
return list;
}
}23.?二叉搜索树的后序遍历序列?
描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。(ps:我们约定空树不是二叉搜索树)
分析
注意二叉搜索树的特点,即?若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence.length == 0)
return false;
return judge(sequence, 0, sequence.length-1);
}
public boolean judge(int[] sequence, int start, int end)
{
if (start >= end)
return true;
int i = end;
while(i >= start && sequence[i] >= sequence[end])
i--;
if (i < 0)
return true;
for (int j=i; j>=start; j--)
{
if (sequence[j] > sequence[end])
return false;
}
return judge(sequence, start, i) && judge(sequence, i+1, end-1);
}
}
24.?二叉树中和为某一值的路径
描述
输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
分析
使用递归
public class Solution {
ArrayList<ArrayList<Integer>> list = new ArrayList<>();
ArrayList<Integer> path = new ArrayList<>();
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
if (root == null || target < root.val)
return list;
path.add(root.val);
target -= root.val;
if (target == 0 && root.left == null && root.right == null)
//如果为list.add(path)则会将多个可能的路径的root值混到一个path中
list.add(new ArrayList<Integer>(path));
FindPath(root.left, target);
FindPath(root.right, target);
//注意此处为什么要remove?
path.remove(path.size()-1);
return list;
}
}?
25.?复杂链表的复制
描述
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)。?下图是一个含有5个结点的复杂链表。图中实线箭头表示next指针,虚线箭头表示random指针。为简单起见,指向null的指针没有画出。
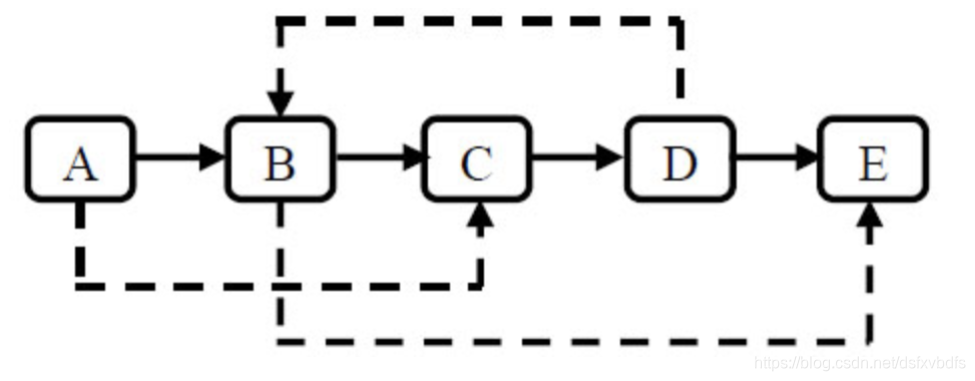
分析
1.复制一个克隆链表,并且克隆元素插入在老链表之间。
2.实现克隆链表的深拷贝
3.分离老链表与克隆链表
public class Solution {
public RandomListNode Clone(RandomListNode pHead) {
if(pHead == null)
return null;
//复制每一个原来的节点,并且将复制节点插入在原节点之后,然后让复制节点指向
//原节点指向的节点
RandomListNode currentNode = pHead;
while(currentNode != null)
{
RandomListNode cloneNode = new RandomListNode(currentNode.label);
RandomListNode nextNode = currentNode.next;
currentNode.next = cloneNode;
cloneNode.next = nextNode;
currentNode = nextNode;
}
//复制每一个原来节点的随机指针给复制节点
currentNode = pHead;
while(currentNode != null)
{
//如果原来节点存在随机指针则将其指向的节点的next节点(即为复制节点
//的随机指针的指向)赋值给原来节点的复制节点的随机指针
if (currentNode.random == null)
currentNode.next.random = null;
else
currentNode.next.random = currentNode.random.next;
currentNode = currentNode.next.next;
}
//拆分原来的链表和复制后的链表
currentNode = pHead;
RandomListNode cloneNode = currentNode.next;
//注意下面原链表和克隆链表的头指针一起移动
while (currentNode != null)
{
RandomListNode cloneNode2 = currentNode.next;
currentNode.next = cloneNode2.next;
if (cloneNode2.next == null)
cloneNode2.next = null;
else
cloneNode2.next = cloneNode2.next.next;
currentNode = currentNode.next;
}
return cloneNode;
}
}?