[数据结构与算法]强化学习入门3—动态规划

前言

本文为强化学习入门系列的第三篇，主要介绍如何通过动态规划来求解贝尔曼最优方程。

我们知道最优策略 $\pi$ 对应的就是最优价值函数，而其求解分为策略迭代、价值迭代两种方法。本节将详细介绍这两种方法。

本节所讨论的MDP都是已知的MDP。已知的意思就是环境的动态特性是已知的，也就是 $p(s^{\prime },a|s,a)$ 这个概率密度函数是确定的。

动态规划

策略迭代

策略迭代可以分为策略评估和策略改进两步骤。策略评估就是给定一个策略 $\pi$ 求解状态价值函数 $v_{\pi }(s)$ ，而策略改进就是寻求一个更优的策略 ${\pi }^{\prime }$，使得 $v_{{\pi }^{\prime }}(s)>v_{\pi }(s)$。

策略评估 Policy Evaluation

解析解推导

策略评估就是给定一个策略 $\pi$ 求解贝尔曼方程 $v_{\pi }(s)$ 。我们知道贝尔曼方程有如下形式：
$$v_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],?s\in S$$
我们把 $v_{\pi }(s),v_{{\pi }^{\prime }}(s)$ 看成未知的，那其实可看出 $v_{\pi }(s),v_{{\pi }^{\prime }}(s)$ 之间是线性关系。因为状态 $s$ 是有多个，所以 $v_{\pi }(s)$ 可写成向量形式：
$$v_{\pi }(s)={?\begin{array}{c}{v}_{\pi }(s_1)\\ v_{\pi }(s_2)\\ ...\\ v_{\pi }(s_S)\end{array}?}_{|S|\times 1}$$
那问题实际上就是求解一个有 $|S|$ 个未知量的线性方程组。我们用矩阵来表示 $v_{\pi }(s),v_{{\pi }^{\prime }}(s)$ 之间的关系，显然矩阵应该是 $S\times S$ 维的。那接下来我们进一步化简方程组，方程组可拆开成如下两部分：
$$v_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)?r+\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)?\gamma v_{\pi }(s^{\prime }),?s\in S$$
观察式子左边项，其实$s^{\prime }$可以被积分掉，也就变成 $\sum_{r}p(r|s,a)r $ ，这就是一个期望的形式，把它定义成一个奖励函数 $r(s,a)$，表示给定策略 $\pi$ 下，状态 $s$ 下采取动作 $a$ 时的期望奖励。那左边项就变成 ${\sum }_a\pi (a|s)?r(s,a)$。我们知道 $\pi$ 是关于a的一个概率分布，那对a积分，则可以把a消掉，左边项最终可以写成 $r_{\pi }(s)$。$r_{\pi }(s)$ 是一个 $|S|\times 1$ 的矩阵。

再来观察式子右边项，$\gamma$ 是一个常数，把r积分掉，则变成 $\gamma {\sum }_a{\sum }_{s^{\prime }}\pi (a|s)p(s^{\prime }|s,a)v_{\pi }(s^{\prime })$，令 $P_{\pi }(s,s^{\prime })={\sum }_a{\sum }_{s^{\prime }}\pi (a|s)p(s^{\prime }|s,a)$，表示状态 $s,s^{\prime }$ 之间的转移概率矩阵，维度为 $|S|\times |S|$。那么右边项最终可写成 $\gamma P_{\pi }(s,s^{\prime })v_{\pi }(s^{\prime })$。

最后，式子化简为：
$$\begin{gathered} v_{\pi }(s)=r_{\pi }(s)+\gamma P_{\pi }(s,s^{\prime })v_{\pi }(s^{\prime }) \\ {v}_{\pi }(s_i)=r_{\pi }(s_i)+\gamma \sum _{j=1}^{|S|}{P}_{\pi }(s_i,s_j)v_{\pi }(s_j) \end{gathered}$$
再进一步简写为：
$$v_{\pi }=(I?\gamma P_{\pi }{)}^{?1}{r}_{\pi }$$
这个就是解析解。显然是一个 $|S|\times 1$ 维的矩阵。由于涉及到矩阵运算，时间复杂度为 $O(|S{|}^3)$。

数值解推导

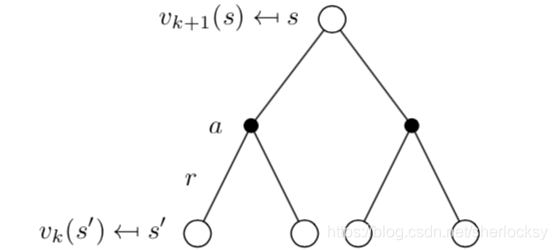
解析解涉及矩阵运算，计算量较大，我们可以通过迭代求数值解。我们构造一个数列 { v k ( s ) } , k ∈ [ 1 , ∞ ] \{v_k(s)\},k\in[1,\infty] {vk?(s)},k∈[1,∞]。其中 $v_k$ 时包含 $|S|$ 个状态价值函数的函数向量。$v_k、v_{k+1}$ 根据贝尔曼方程我们可以写出其迭代关系：
$$\begin{array}{rl}{v}_{k+1}(s)=& E_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ =& E_{\pi }[R_{t+1}+\gamma v_k(s^{\prime })|S_t=s]\\ =& \sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]\end{array}$$
其实 $v_1,v_2,...,v_k$ 是通过迭代求得的价值函数的近似解，我们的目标就是使其收敛到 $v_{\pi }$。这个$v_1$是先通过随机动作来确定的，也就是一个随机的初始函数向量。

策略改进

当我们能估计 ${\pi }^{\prime }$ 时，我们想知道与当前策略 $\pi$ 哪个好，就需要比较 $v_{\pi },v_{{\pi }^{\prime }}$。这就引出了策略改进定理。

策略改进定理 policy improvement theorem

【定义】给定 $\pi ,{\pi }^{\prime }$，如果对于任意状态s，有 $q_{\pi }(s,{\pi }^{\prime }(s))\ge v_{\pi }(s)$，则 $?s\in S,v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s)$。

这个定理把原先需要求两个状态价值函数变成只需求一个 $v_{\pi }(s)$ 就好。

那如何证明？

我们先回顾动作价值函数：
$$q_{\pi }(s,a)=E[R_{t+1}+\gamma ?v_{\pi }(S_{t+1})|S_t=s,A_t=a]=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$$
值得注意的是，$R_{t+1}$ 和 $\pi$ 其实是无关的，因为在(s,a)时，平均奖励 $R_{t+1}$ 已经获得了，而 $\pi$ 影响的是下一时刻的状态 $s_{t+1}$ 对于动作的选择，$R_{t+2}$ 和 $\pi$ 才有关。

我们把 ${\pi }^{\prime }(s)$ 代入动作 $a$，表示 $t$ 时刻的动作是由 ${\pi }^{\prime }$ 确定的，下一时刻的动作还是由 $\pi$ 确定，所以 $R_{t+1}$ 和 ${\pi }^{\prime }$ 有关，之后的奖励和 $\pi$ 有关，推导过程如下：
$$\begin{array}{rl}{v}_{\pi }(s)\le & q_{\pi }(s,{\pi }^{\prime }(s))\\ =& E[R_{t+1}+\gamma ?v_{\pi }(S_{t+1})|S_t=s,A_t={\pi }^{\prime }(s)]\\ =& E_{{\pi }^{\prime }}[R_{t+1}+\gamma ?v_{\pi }(S_{t+1})|S_t=s]\\ \le & E_{{\pi }^{\prime }}[R_{t+1}+\gamma ?q_{\pi }(S_{t+1},{\pi }^{\prime }(S_{t+1}))|S_t=s]\\ \le & E_{{\pi }^{\prime }}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2?q_{\pi }(S_{t+2},{\pi }^{\prime }(S_{t+2}))|S_t=s]\\ \le & E_{{\pi }^{\prime }}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+...|S_{t+1}=s]\\ =& v_{{\pi }^{\prime }}(s)\end{array}$$
有了这一定理，我们怎么寻找最优的策略？一种比较直观的方法就是贪心方法。

对每个状态s，都选取其动作价值函数最大的的策略 ${\pi }^{\prime }$，即
$$?s\in S,{\pi }^{\prime }(s)=\arg \underset{a}{\max }{q}_{\pi }(s,a)==\arg \underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$$
根据策略改进定理，如果 $q_{\pi }(s,{\pi }^{\prime }(s))\ge v_{\pi }(s)$，则更新策略。直到某一时刻下 $v_{{\pi }^{\prime }}(s)=v_{\pi }(s)$ 时，则算法已收敛，这时也满足贝尔曼最优方程，此时的策略就是我们的最优策略。

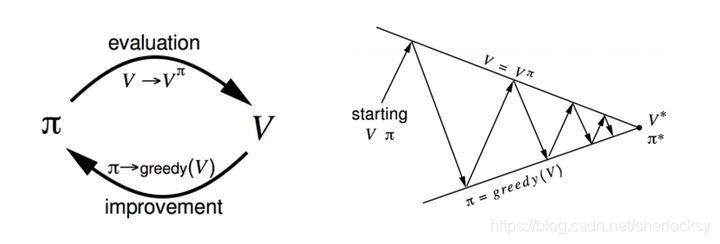
简单的流程图如下：

价值迭代

在策略迭代中，我们每轮迭代的步骤是：先根据 $\pi$ 评估 $v_{\pi }(s)$，再采用贪心方法改进策略。但是在策略评估时，为了使价值函数收敛到 $v_{\pi }$ 我们需要对所有状态都迭代若干次直到价值函数收敛，这就造成迭代中套娃迭代，计算非常麻烦。

那能不能减少迭代呢？有一个方法就是，在评估时只进行一次迭代，也就是对所有状态只扫描一次，接着进行策略改进。

$$\begin{array}{rl}{v}_{k+1}(s)=& \underset{a}{\max }{E}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ =& \underset{a}{\max }{E}_{\pi }[R_{t+1}+\gamma v_k(s^{\prime })|S_t=s]\\ =& \underset{a}{\max }\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]\end{array}$$

那这个其实就是贝尔曼最优方程。这样子就不需要反复迭代来求解 $v_{\pi }(s)$了。

从过程来理解价值迭代与策略迭代的不同

• 价值迭代的过程是: $v_1\to v_2\to v_3\to ...\to v_{?}$

• 策略迭代的过程是: ${\pi }_1\to v_{{\pi }_1}\to {\pi }_2\to v_{{\pi }_2}\to {\pi }_3\to v_{{\pi }_3}\to ...\to {\pi }_{?}\to v_{?}$

显然，策略迭代需要先求精确的状态价值函数 ，然后不停更新策略。一次更新是对整个状态空间进行遍历。而价值迭代是在一次遍历后立即停止策略评估，这样对每个状态只进行一次更新，计算的是近似的价值函数。

价值迭代虽然计算简化，但仍需遍历一次状态空间，这种方法其实也称为同步动态规划（Synchronous DP）。

事实上，还有一种更为简化的方法叫做就地策略迭代。属于异步动态规划Asynchronous DP方法。即我们并不需要保持所有状态更新的同步，在某次更新中，不对状态集合 S 中的每一个状态都更新，而只随机选取其中的某一个状态的价值函数进行更新，其他状态保持不变 。这样减小计算，可以更快的达到收敛。

小结

本节介绍了如何用动态规划求解最优策略。动态规划是属于在model-based的情况下的算法，因为我们已经假定了环境的动态特性是已知的。动态规划分为策略迭代和价值迭代。策略迭代又分为两个步骤，一个是策略评估，一个是策略改进。策略评估用于计算给定策略的价值函数，属于精确计算。策略改进利用策略改进定理比较两个策略的价值函数，从而对策略进行更新。策略评估需要迭代计算，而策略迭代本身也是个迭代的过程，涉及到迭代中的迭代，造成计算非常复杂，于是就有了价值迭代。价值迭代可看出是特殊的策略迭代，其主要思想是在计算价值函数时只迭代一步，近似计算价值函数。价值迭代也称为同步动态规划。尽管计算简化，但价值迭代中对状态空间的每个状态都要更新一次，仍需遍历一次状态空间。为此，就有人提出异步的迭代思路——就地策略迭代。即我们并不需要保持所有状态更新的同步，在某次更新中，不对状态集合 S 中的每一个状态都更新，而只随机选取其中的某一个状态的价值函数进行更新，其他状态保持不变 。

参考

[1] sutton.Barto.《强化学习(第二版)》

[2] 动态规划——强化学习第四章 - 知乎 (zhihu.com)

[2] 【机器学习】白板推导系列(三十五) ～ 强化学习之动态规划_bilibili