[数据结构与算法]Dinic求最大流

Dinic求最大流

题目描述

核心思路

Dinic算法思想：首先通过广度优先搜索将图中的顶点分层，然后通过深度优先搜索，沿着层次增1并且$flow<limit$的方向寻找增广路，回溯时增流。一次深度优先搜索可以找到多条增广路径，实现多次增流，这正是Dinic算法的巧妙之处。

算法步骤：

• 在残留网络上BFS求出各个顶点的层次，构造分层图
• 在分层图上进行DFS，沿着层次增1并且$flow<limit$的方向寻找增广路径，在回溯时实现更新剩余容量。另外每个点可以流向多条边，因此还可以同时加入剪枝优化
• 重复以上步骤，直到不存在增广路径为止

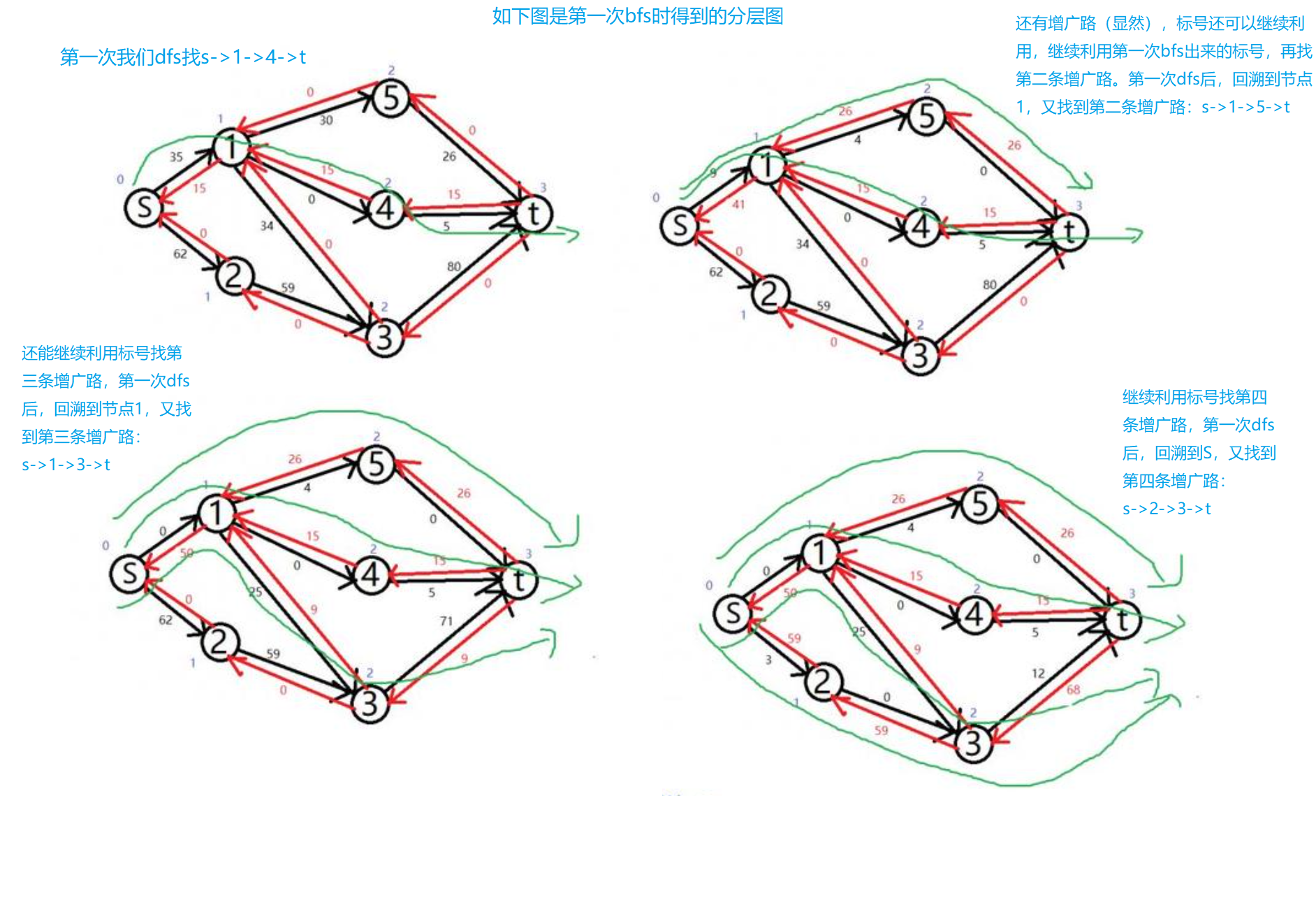
如何理解一次深度优先搜索可以找到多条增广路径呢？

如下图所示：

我们可以利用一次bfs得到的分层图，然后对这个分层图进行一次dfs，就可以直接得出四条增广路径！！！

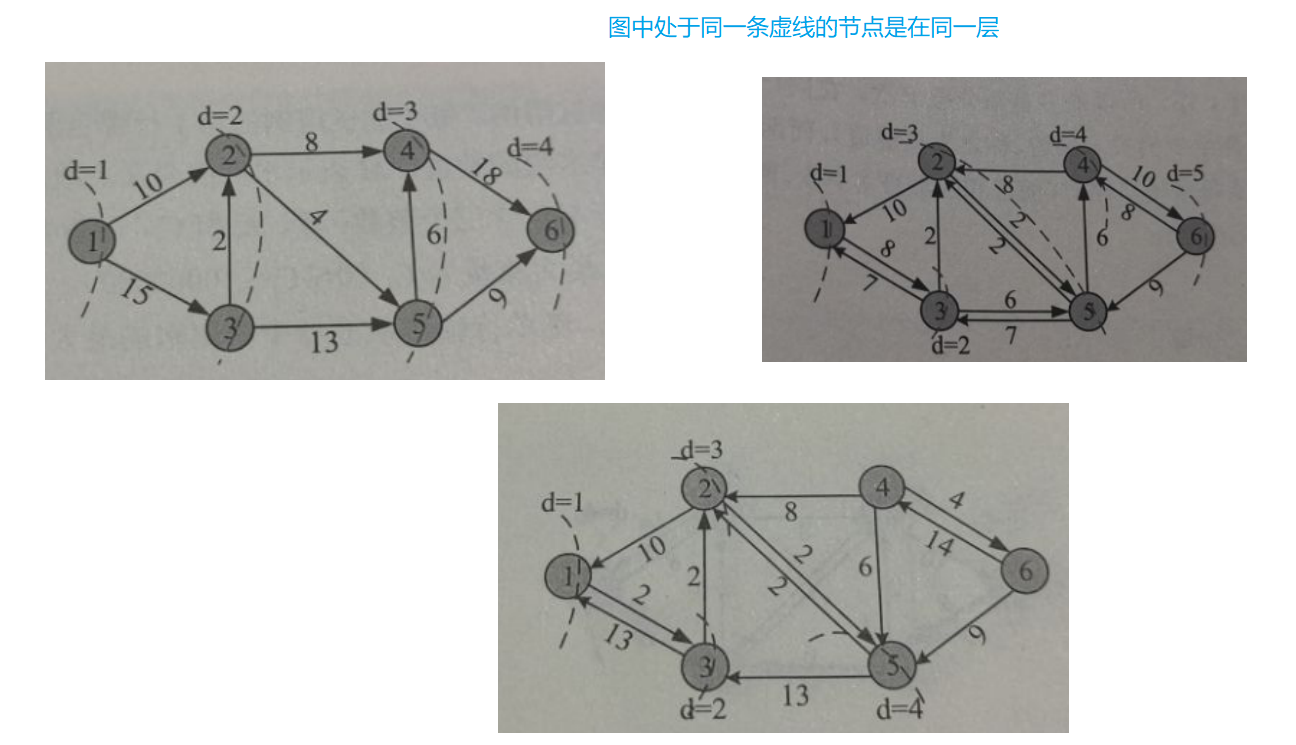
Dinic算法在执行过程中每次都要重新分层，从源点到汇点的层次是严格递增的，包含$V$个点的层次图最多有$V$层，所以最多重新分层$V$次。

如何理解limit和flow变量呢？

limit表示从起点走到当前点$u$的路径的容量上限，我们要在满足这个限制的基础上，求出从当前点到汇点的最大流量。flow表示从当前点$u$出发，往后面流出的流量。

如何理解$flow<limit$呢？

• 假设$flow>limit$，根据流量守恒可知，这个是绝对不可能的，从起点$S$流到当前点的最大容量是$limit$，那么从当前点$u$流出去的容量不可能超过$limit$
• 假设$flow=limit$，在一些数据中，如果在一次增广中$flow$刚好等于$limit$，就会继续跑下去，在下一层，开始是我们初始化了$flow=0$，假设经过上一层之后，传到下一层的$limit=0$，那么如果写成$flow\le limit$，此时就会进入for循环中，又会继续跑下去，就一直调用find函数了，最后就跑不完了。
• 综上，我们需要写成$flow<limit$

如何理解当前弧优化呢？

如图所示：

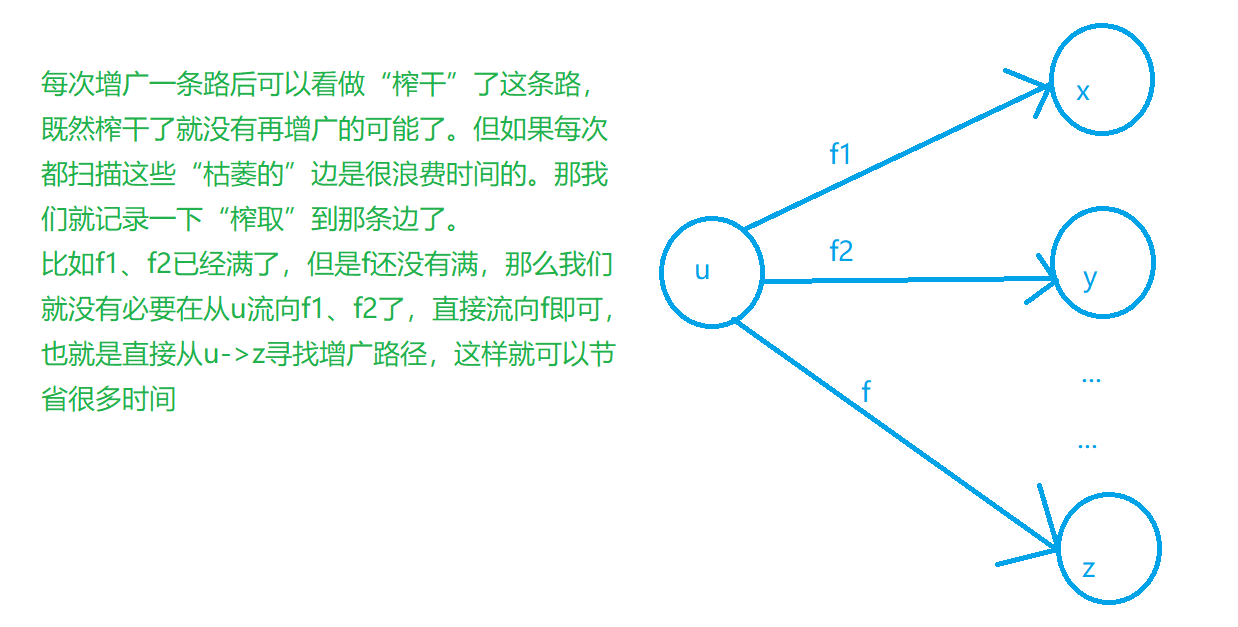
我们定义一个数组cur记录当前边（弧）（功能类比邻接表中的h数组，只是会随着dfs的进行而修改），每次我们找过某条边（弧）时，修改cur数组，改成该边（弧）的编号，那么下次到达该点时，会直接从cur对应的边开始（也就是说从h到cur中间的那一些边（弧）我们就不走了）。首先，我们在按顺序dfs时，先被遍历到的边肯定是已经增广过了（或者已经确定无法继续增广了），那么这条边就可以视为“废边”。那么下次我们再到达该节点时，就可以直接无视掉所有废边，只走还有用的边，也就是说，每次dfs结束后，下次dfs可以更省时间。

int find(int u, int limit)
{
    if (u == T) return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = ne[i])
    {
        cur[u] = i;  // 当前弧优化
        int ver = e[i];
        if (d[ver] == d[u] + 1 && f[i])
        {
            int t = find(ver, min(f[i], limit - flow));
            if (!t) d[ver] = -1;
            f[i] -= t, f[i ^ 1] += t, flow += t;
        }
    }
    return flow;
}

代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10010,M=2e5+10,INF=1e8;
int n,m,S,T;
//f[i]是i这条边上的容量
int h[N],e[M],ne[M],f[M],idx;
//q是宽搜存放节点的队列
//d[i]=1表示i这个节点是在第一层  记录每个节点处于哪一个层次
//cur数组 是用来 当前边优化
int q[N],d[N],cur[N];

void add(int a,int b,int c)
{
    e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
    e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

bool bfs()
{
    memset(d,-1,sizeof d);  //初始化层次为-1
    int hh=0,tt=0;
    //起点的层次属于第0层
    q[0]=S,d[S]=0,cur[S]=h[S];
    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=h[t];~i;i=ne[i])
        {
            int ver=e[i];
            //d[ver]==-1表示ver这个点还没有访问过 没有被分层
            if(d[ver]==-1&&f[i])
            {
                d[ver]=d[t]+1;
                cur[ver]=h[ver];
                if(ver==T)
                    return true;
                q[++tt]=ver;
            }
        }
    }
    return false;
}
//u是当前节点
//limit表示从起点走到当前点的路径的容量上限
// 我们要在满足这个限制的基础上,求出从当前点到汇点的最大流量
int find(int u,int limit)
{
    //如果u等于T了,那么则找到了从源点S到汇点T的最大流 此时答案就是limit
    if(u==T)
        return limit;
    //flow表示u节点之后可以流出的流量
    int flow=0;
    //遍历节点u的所有邻接点
    for(int i=cur[u];~i&&flow<limit;i=ne[i])//i是边
    {
        cur[u]=i;//当前弧优化
        int ver=e[i];
        if(d[ver]==d[u]+1&&f[i])
        {
            //由于从点u往后已经输送了flow的流量 那么此时还可以从源点S输出的流量为limit-flow
            //f[i]表示i这条水管的容量 我们应该取f[i]和limit-flow的最小值
            //如果limit-flow>f[i],则这条水管不够容纳 会爆掉
            int t=find(ver,min(f[i],limit-flow));
            //如果t为0 则说明从节点ver往后已经没有可以流出的流量了
            //那么从ver往后就不能找到一条增广路径了 直接d[ver]=-1;进行剪枝
            if(!t)
                d[ver]=-1;
            f[i]-=t;        //更新正向边的容量
            f[i^1]+=t;      //更新反向边的容量
            flow+=t;        //往后输出的流量又增加了t
        }
    }
    return flow;
}
int dinic()
{
    int maxflow=0;      //最大流
    int flow;
    while(bfs())//执行bfs构建分层图
    {
        //对这张分层图进行dfs 寻找增广路径计算出可行流
        while(flow=find(S,INF))
            maxflow+=flow;      //累加多条可行流 最终得到最大流
    }
    return maxflow;
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d%d%d",&n,&m,&S,&T);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    printf("%d\n",dinic());
    return 0;
}