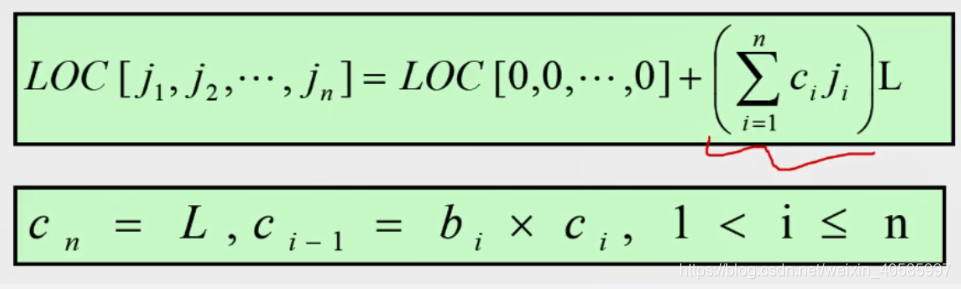串、数组、广义表

线性表、栈、队列都是线性结构，其中栈和队列是操作受限的线性表；
串是内容受限的线性表；数组和广义表 可以看作是线性表的推广

1 概念

1.1 串

串：零个或多个任意字符组成的有限序列
子串：串中任意个连续字符组成的子序列称为该串的子串，真子串是不包含自身的所有子串
主串：包含子串的串相应的称为主串
字符位置：字符在序列中的序号
子串位置：子串第一个字符在主串中的位置
空格串：由一个或多个空格组成的串，与空串不同

顺序存储结构用的多！
串的链式存储：操作方便，但是存储密度过低！可将多个字符放在一个结点，以克服其缺点！

1.2 数组

按一定格式排列起来的具有相同类型的数据元素的集合
逻辑结构：线性结构，定长的线性表
声名格式：数据类型，变量名称[长度]
一维数组：~
二维数组：
（1）非线性结构：每一个数据元素既在一个行表中又在一个列表中
（2）线性结构（定长的线性表）：该线性表的每个数据元素也是一个定长的线性表

线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展
数组特点：结构固定，定义后维数和维界不变
基本操作：取元素，修改元素值

计算二维数组元素存储位置：

三维数组：

n维数组:

特殊矩阵的压缩存储：
若多个数据元素的值都相同，则只分配一个元素值的存储空间，且零元素不占存储空间

1.3 广义表

又称列表（List），是n>=0个元素a0,a1,a2…的有限序列，其中每一个ai或者是原子，或者是一个广义表
表头表尾：表尾是除掉表头剩下元素组成的一个子表

广义表中的数据元素有相对次序；一个直接前驱和一个直接后驱
广义表的长度定义为最外层所包含元素的个数
广义表的深度定义为该广义表展开后所含括号的的重数
原子的深度为0，空表的深度为1
广义表可以和其他广义表共享，
广义表是一个多层次的结构，广义表的元素可以是单元素也可以是子表，而子表的元素还可以是子表

2 实现

2.1 串的模式匹配算法

要包含的文件如下，在之前的笔记中均给出了代码！

#pragma once
#include<iostream>
using namespace std;
#include"string"
#include"seqList.hpp"
#include"linkList.hpp"



class LinearTable_Case {

public:
	LinearTable_Case();
	int index_BF(string S, string T);//返回字符串T在S中的位置
	int index_KMP(string S, string T);

	~LinearTable_Case();
};

2.1.1 BF(Brute-Force)算法

亦称简单匹配算法，采用穷举法思路

int LinearTable_Case::index_BF(string S, string T)
{
	int i = 1, j = 1;
	while (i <= S.size() && j <= T.size())
	{
		if (S[i] == T[j])
		{
			i++;//在这里++i和i++效果相同？
			j++;
		}
		else
		{
			i = i - j + 2;
			j = 1;
		}
	}
	if (j >= T.size())
	{
		return i - T.size();
	}
	else
	{
		return 0;
	}

}

2.1.2 KMP算法

int LinearTable_Case::index_KMP(string S, string T)
{
	//先求关于T的next数组
	//cout << T.size() << endl;
	int* next = new int[T.size()];
	int i = 0, j = -1;
	next[0] = -1;
	while (i < T.size())
	{
		if (j == -1 || T[i] == T[j])
		{
			++i;
			++j;
			next[i] = j;

		}
		else
		{
			j = next[j];
		}
	}
	//for (int a = 0; a < T.size();a++)
	//{
	//	cout << next[a] << " " ;
	//}
	//cout << endl;


	//实现KMP算法
	int k = 0, f = 0;
	while (k < S.size() && f < T.size())
	{
		if (f == -1 || S[k] == T[f])
		{
			k++;
			f++;
		}
		else
		{
			f = next[f];
		}
		//cout << "000" << endl;
	}

	if (f == T.size())
	{
		return k - f;
		//cout << "11111" << endl;

	}
	else
	{
		return -1;
	}

}