[数据结构与算法]堆的建立以及排序算法的时间复杂度

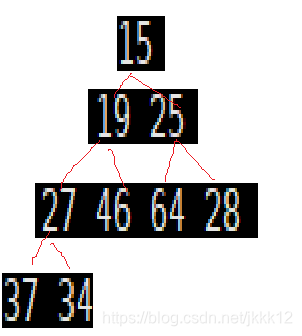
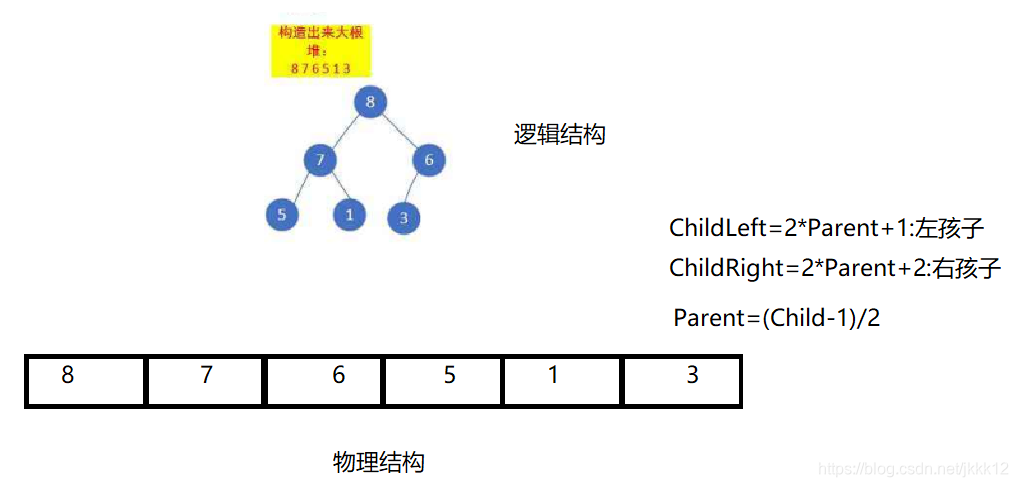
堆其实是完全二叉树，它的逻辑结构是二叉树的形式，而物理结构在内存中是以数组的形式进行存放的如下图所示。同时下面三个公式是父亲节点与孩子节点的相互关系。

堆的实现：如下图所示，我们给一个数组采用向下调整算法对其建小堆，并且向下调整算法是根的左右子树都必须恰都是小堆，才能使用向下调整算法。（建大堆时左右子树都是大堆）
向下调整算法的步骤：
1、通过父亲节点计算出孩子节点然后比较左右孩子的较小的值
2、通过较小孩子与父亲节点比较，如果孩子的值小于父亲的值，则孩子和父亲进行交换，之后将将Parent=Child; Child=2*Parent+1 进行行迭代，直到Parent走到叶子节点就结束了。
3、如果小大孩子比父亲大，那么就不需要调整了，整个树就是小数了。调整如下图。

#include<stdio.h>

void Swap(int* a,int* b)
{
  int temp=*a;
  *a=*b;
  *b=temp;
}

void AdjustDwon(int* a,int n, int parent)
{
  int child=2*parent+1;

  while(child<n)
  {
    if(child+1<n&&a[child]>a[child+1])
    {
      child++;
    }

    if(a[child]<a[parent])
    {
      Swap(&a[child],&a[parent]);
      parent=child;
      child=2*parent+1;
    }
    else 
    {
      break;
    }
  }
}

void Printf(int* a,int n)
{
  int i=0;
  for(i=0;i<n;i++)
  {
    printf("%d ",a[i]);
  }
  printf("\n");
}
int main()
{

  int a[]={27,15,19,18,28,34,65,49,25,37};
  int n=sizeof(a)/sizeof(a[0]);
  Printf(a,n);
  AdjustDwon(a,n,0);
  Printf(a,n);


  return 0;

}

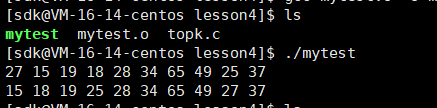
程序运行如下：可以看到经过向下调整后变成了一个小堆。

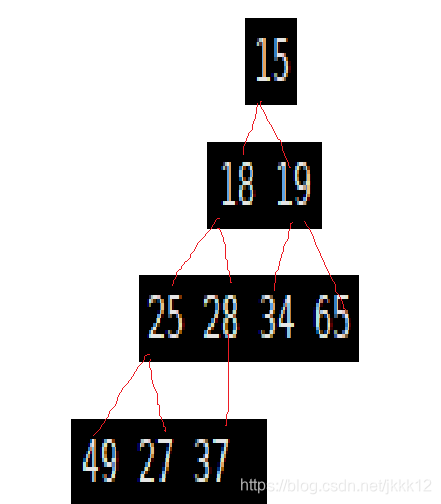
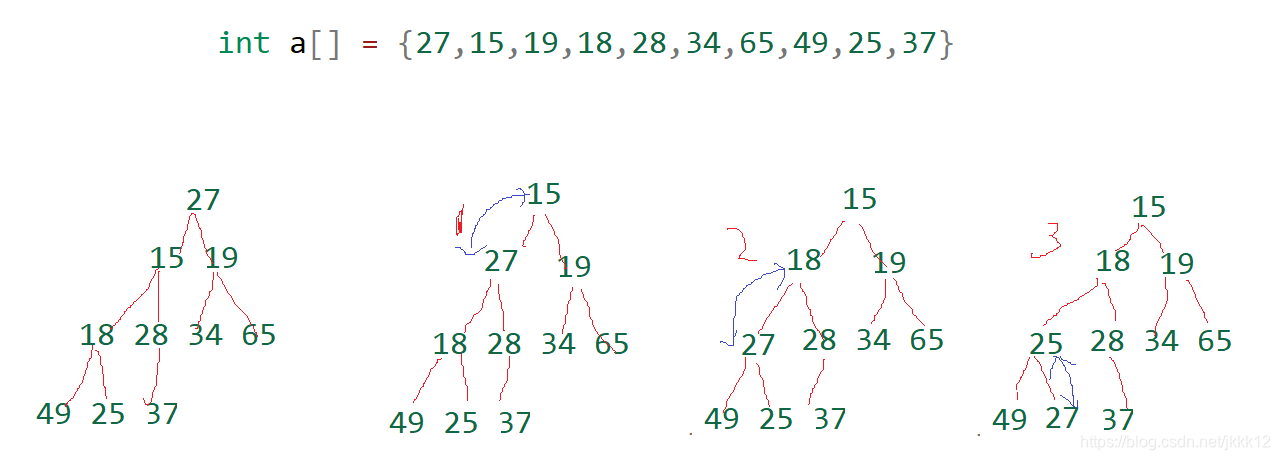
如果我们给的数据的根节点不是左右子树呢，我们应该如何建堆，我们可以从倒数的第一个非叶子节点，按编号，依次作为子树去向下调整

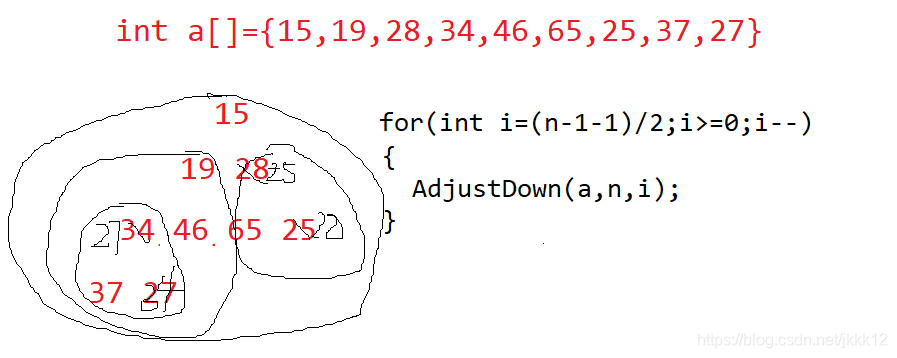
程序运行的结果：