找到最终安全状态
题目
在有向图中,以某个节点为起始节点,从该点出发,每一步沿着图中的一条有向边行走。如果到达的节点是终点(即它没有连出的有向边),则停止。
对于一个起始节点,如果从该节点出发,无论每一步选择沿哪条有向边行走,最后必然在有限步内到达终点,则将该起始节点称作是 安全 的。
返回一个由图中所有安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。
该有向图有 n 个节点,按 0 到 n - 1 编号,其中 n 是 graph 的节点数。图以下述形式给出:graph[i] 是编号 j节点的一个列表,满足 (i, j) 是图的一条有向边。
示例 1:
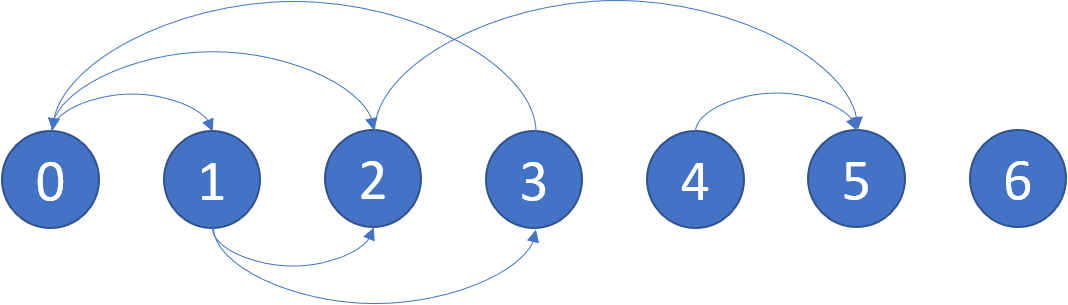
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
解释:示意图如上。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出:[4]
提示:
n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 [1, 4 * 104] 内。
官方题解1
深度优先搜索 + 三色标记法
根据题意,若起始节点位于一个环内,或者能到达一个环,则该节点不是安全的。否则,该节点是安全的。
我们可以使用深度优先搜索来找环,并在深度优先搜索时,用三种颜色对节点进行标记,标记的规则如下:
白色(用 0 表示):该节点尚未被访问; 灰色(用 1 表示):该节点位于递归栈中,或者在某个环上; 黑色(用 2 表示):该节点搜索完毕,是一个安全节点。
当我们首次访问一个节点时,将其标记为灰色,并继续搜索与其相连的节点。
如果在搜索过程中遇到了一个灰色节点,则说明找到了一个环,此时退出搜索,栈中的节点仍保持为灰色,这一做法可以将「找到了环」这一信息传递到栈中的所有节点上。
如果搜索过程中没有遇到灰色节点,则说明没有遇到环,那么递归返回前,我们将其标记由灰色改为黑色,即表示它是一个安全的节点。
代码 + 注释
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>> &graph) {
// 获得结点个数
int n = graph.size();
// 建立颜色 0表示白色, 1表示灰色, 2表示黑色
vector<int> color(n);
function<bool(int)> safe = [&](int x) {
// 首先判断该结点是否被访问过
// 如果访问过直接返回, true表示安全结点, false表示不安全结点
if (color[x] > 0) {
return color[x] == 2;
}
// 若结点未被访问过,先赋值为1,表示位于递归栈上
color[x] = 1;
// 对该结点中的没一个结点进行递归,直到终点
for (int y : graph[x]) {
// 只要递归过程中出现一次不安全结点,则返回false, 表示结点不安全
if (!safe(y)) {
return false;
}
}
// 若递归结束未返回false, 则证明该结点是安全结点, 赋值为2
color[x] = 2;
return true;
};
vector<int> ans; // 最终的安全结点
for (int i = 0; i < n; ++i) {
if (safe(i)) {
ans.push_back(i);
}
}
// 返回安全结点
return ans;
}
};
官方题解2
拓扑排序
根据题意,若一个节点没有出边,则该节点是安全的;若一个节点出边相连的点都是安全的,则该节点也是安全的。
根据这一性质,我们可以将图中所有边反向,得到一个反图,然后在反图上运行拓扑排序。
具体来说,首先得到反图rg 及其入度数组 inDeg。将所有入度为 0的点加入队列,然后不断取出队首元素,将其出边相连的点的入度减一,若该点入度减一后为0,则将该点加入队列,如此循环直至队列为空。循环结束后,所有入度为 0 的节点均为安全的。我们遍历入度数组,并将入度为 0的点加入答案列表。
代码 + 注释
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>> &graph) {
int n = graph.size();
// 建立一个新图, 存储反图
vector<vector<int>> rg(n);
// 存储反图中每一个节点的入度
vector<int> inDeg(n);
// 反图生成
for (int x = 0; x < n; ++x) {
for (int y : graph[x]) {
rg[y].push_back(x);
}
// 原图中各结点的大小就代表着反图中该结点的入度
inDeg[x] = graph[x].size();
}
// 排序队列
queue<int> q;
// 将反图中所有入度为0的结点入队,存储下标
for (int i = 0; i < n; ++i) {
if (inDeg[i] == 0) {
q.push(i);
}
}
// 拓扑
while (!q.empty()) {
// 不断取出队首元素,将其出边相连的点的入度减一
int y = q.front();
q.pop();
// 若该点入度减一后为00,则将该点加入队列,如此循环直至队列为空。
for (int x : rg[y]) {
if (--inDeg[x] == 0) {
q.push(x);
}
}
}
vector<int> ans;
// 所有入度为0的结点即为安全结点,用下标表示
for (int i = 0; i < n; ++i) {
if (inDeg[i] == 0) {
ans.push_back(i);
}
}
return ans;
}
};
注:所有题目以及代码均来自力扣,我只是对代码进行了注释,有时候会有一些自己的改动,加了一些自己的理解,仅供自己学习使用。如果大家对我的注释有什么疑问或者指正,欢迎大家一起讨论。