1. 定义结点

??二叉树结点和普通树节点的定义：

struct binaryTreeNode {
	binaryTreeNode(int x = 0) :data(x), lchild(nullptr), rchild(nullptr) {}
	binaryTreeNode* lchild, *rchild;
	int data;
};
struct treeNode {
	treeNode(int x = 0) :data(x) {}
	vector<treeNode*> children;
	int data;
};

??二叉树每个节点最多有两个子节点，节点的指针域使用两个结点指针就行。普通树每个节点的子节点数任意，我们使用 vector 存放指向子节点的指针，这样就可以使用 vector 的迭代器遍历子节点，当然普通树的指针域也可以使用链表实现。

2. 创建树

??创建图 1 所示的二叉树和普通树。普通树的 a 节点值为 1，b 节点值为 2，以此类推。

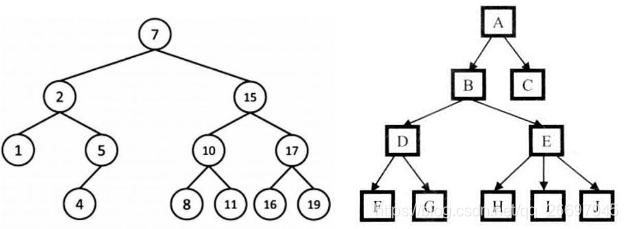
$图 1$

binaryTreeNode* build_binary_tree() {
	const int n = 12;
	int a[n] = { 1,2,4,5,7,8,10,11,15,16,17,19 };
	binaryTreeNode* nodes[n];
	for (int i = 0; i < n; i++)
		nodes[i] = new binaryTreeNode(a[i]);
	nodes[3]->lchild = nodes[2];
	nodes[1]->lchild = nodes[0];
	nodes[1]->rchild = nodes[3];
	nodes[4]->lchild = nodes[1];
	nodes[4]->rchild = nodes[8];
	nodes[8]->lchild = nodes[6];
	nodes[8]->rchild = nodes[10];
	nodes[6]->lchild = nodes[5];
	nodes[6]->rchild = nodes[7];
	nodes[10]->lchild = nodes[9];
	nodes[10]->rchild = nodes[11];
	return nodes[4];
}
treeNode* build_tree() {
	treeNode* a = new treeNode(1);
	treeNode* b = new treeNode(2);
	treeNode* c = new treeNode(3);
	a->children.push_back(b);
	a->children.push_back(c);
	treeNode* d = new treeNode(4);
	treeNode* e = new treeNode(5);
	b->children.push_back(d);
	b->children.push_back(e);
	treeNode* f = new treeNode(6);
	treeNode* g = new treeNode(7);
	d->children.push_back(f);
	d->children.push_back(g);
	treeNode* h = new treeNode(8);
	treeNode* i = new treeNode(9);
	treeNode* j = new treeNode(10);
	e->children.push_back(h);
	e->children.push_back(i);
	e->children.push_back(j);
	return a;
}

3. 先序、中序、后序的递归算法

??二叉树有层序遍历、先序遍历、中序遍历、后序遍历。普通树没有中序遍历，其它 3 种遍历方式都有。

// 3.1 先序递归遍历
void pre_recurse_traverse_binary_tree(binaryTreeNode* tree) {
	if (tree == nullptr)
		return;
	cout << tree->data << ' ';
	pre_recurse_traverse_binary_tree(tree->lchild);
	pre_recurse_traverse_binary_tree(tree->rchild);
}
void pre_recurse_traverse_tree(treeNode* tree) {
	if (tree == nullptr)
		return;
	cout << tree->data << " ";
	for (auto it : tree->children)
		pre_recurse_traverse_tree(it);
}
// 3.2 中序递归遍历
void in_recurse_traverse_binary_tree(binaryTreeNode* tree) {
	if (tree == nullptr)
		return;
	in_recurse_traverse_binary_tree(tree->lchild);
	cout << tree->data << ' ';
	in_recurse_traverse_binary_tree(tree->rchild);
}
// 3.3 后序递归遍历
void post_recurse_traverse_binary_tree(binaryTreeNode* tree) {
	if (tree == nullptr)
		return;
	post_recurse_traverse_binary_tree(tree->lchild);
	post_recurse_traverse_binary_tree(tree->rchild);
	cout << tree->data << ' ';
}
void post_recurse_traverse_tree(treeNode* tree) {
	if (tree == nullptr)
		return;
	for (auto it : tree->children)
		post_recurse_traverse_tree(it);
	cout << tree->data << " ";
}

4. 先序、中序、后序的非递归算法

// 4.1 先序非递归遍历
void pre_traverse_binary_tree(binaryTreeNode* tree) {
	if (tree == nullptr)
		return;
	stack<binaryTreeNode*> st;
	st.push(tree);
	while (st.empty() != true) {
		tree = st.top();
		st.pop();
		cout << tree->data << " ";
		if (tree->rchild != nullptr) st.push(tree->rchild);
		if (tree->lchild != nullptr) st.push(tree->lchild);
	}
	cout << endl;
}
void pre_traverse_tree(treeNode* tree) {
	if (tree == nullptr)
		return;
	stack<treeNode*> st;
	st.push(tree);
	while (st.empty() != true) {
		tree = st.top();
		st.pop();
		cout << tree->data << " ";
		for (auto it = tree->children.rbegin(); it != tree->children.rend(); it++)
			st.push(*it);
	}
	cout << endl;
}
// 4.2 中序非递归遍历
void in_traverse_binary_tree(binaryTreeNode* tree) {
	stack<binaryTreeNode*> st;
	while (tree != nullptr || st.empty() != true) {
		while (tree != nullptr) {
			st.push(tree);
			tree = tree->lchild;
		}
		tree = st.top();
		st.pop();
		cout << tree->data << ' ';
		tree = tree->rchild;
	}
	cout << endl;
}
// 4.3 后序非递归遍历
void post_traverse_binary_tree(binaryTreeNode* tree) {
	binaryTreeNode* lastVisit = nullptr;
	stack<binaryTreeNode*> st;
	while (tree != nullptr || st.empty() != true) {
		while (tree != nullptr) {
			st.push(tree);
			tree = tree->lchild;
		}
		tree = st.top();
		st.pop();
		if (tree->rchild == nullptr || tree->rchild == lastVisit) {
			cout << tree->data << ' ';
			lastVisit = tree;
			tree = nullptr;
		}
		else {
			st.push(tree);
			tree = tree->rchild;
		}
	}
	cout << endl;
}
vector<int> post_traverse_tree(treeNode* tree) {
	if (tree == nullptr)
		return{};
	vector<int> res;
	stack<treeNode*> st;
	st.push(tree);
	while (st.empty() != true) {
		tree = st.top();
		st.pop();
		res.push_back(tree->data);
		for (auto &x : tree->children)
			st.push(x);
	}
	reverse(res.begin(), res.end());
	return res;
}

??先序遍历：因为我们使用栈，后入栈的先访问。而且先序遍历时，遍历了一个结点接着就会遍历它的左右子结点，所以遍历一个结点后就把它的子结点从右向左依次进栈。如第 11、12 行和第 25、26 行。
??后序遍历：使用了辅助空间 res。最终的结果是 res 的逆序，如第 81 行。

5. 层序遍历

void layer_traverse_binary_tree(binaryTreeNode* tree) {
	if (tree == nullptr)
		return;
	queue<binaryTreeNode*> qu;
	qu.push(tree);
	while (qu.empty() != true) {
		tree = qu.front();
		qu.pop();
		cout << tree->data << " ";
		if (tree->lchild != nullptr) qu.push(tree->lchild);
		if (tree->rchild != nullptr) qu.push(tree->rchild);
	}
	cout << endl;
}
void layer_traverse_tree(treeNode* tree) {
	if (tree == nullptr)
		return;
	queue<treeNode*> qu;
	qu.push(tree);
	while (qu.empty() != true) {
		tree = qu.front();
		qu.pop();
		cout << tree->data << " ";
		for (auto it : tree->children)
			qu.push(it);
	}
	cout << endl;
}

6. 求根节点到指定节点路径的递归算法

bool get_path_binary_tree(binaryTreeNode* tree, int node, list<binaryTreeNode*>& path) {
	if (tree == nullptr)
		return false;
	if (tree->data == node)
		return true;

	// found = true：子树包含结点node。
	path.push_back(tree);
	bool found = false;
	found = get_path_binary_tree(tree->lchild, node, path);
	if (found == false)
		found = get_path_binary_tree(tree->rchild, node, path);
	if (found == false)
		path.pop_back();

	return found;
}
bool get_path_tree(treeNode* tree, int node, list<treeNode*>& path) {
	if (tree == nullptr)
		return false;
	if (tree->data == node)
		return true;

	// found = true：子树包含结点node。
	path.push_back(tree);
	bool found = false;
	for (auto it : tree->children) {
		found = get_path_tree(it, node, path);
		if (found == true)
			break;
	}
	if (found == false)
		path.pop_back();

	return found;
}

??找到的从 tree 节点到 node 节点的路径的最后一个节点是 node 节点的父节点，不包括 node 节点。只需要把第 8、25 行分别移到第 3、4 行和第 20、21 行之间即可使路径包括 node 结点。
??上面二叉树和普通树的算法相同，仅仅因为二叉树结点和普通树结点的子结点数目不同引起查找子树有略微差异，如第 10 至 12 行与第 27 至第 31 行分别是在二叉树结点 tree 的子树中查找 node 和在普通树结点 tree 的子树中查找 node。
??函数的第一个参数是根结点 tree，返回值为 true 说明以 tree 为根节点的子树中包含 node 节点。
??以二叉树为例，第 2 行和第 4 行是递归终止条件。第 2 行：找到叶结点还没有找到 node，则 node 不在以 tree 为根节点的子树中，返回 false；第 4 行找到了 node 结点返回 true。没有到达终止条件时，先暂且认为 tree 是路径上的结点，如第 8 行。判断 tree 的子树中有没有 node 结点，found 为 true 说明 tree 的子树有 node 结点，则以 tree 为根节点的子树也有 node，返回 true。found 为 false 说明没有，则 tree 不在路径上，把它从路径中移除，如第 14 行。