二叉树的属性

文章目录

二叉树的属性

1. “101. 对称二叉树”

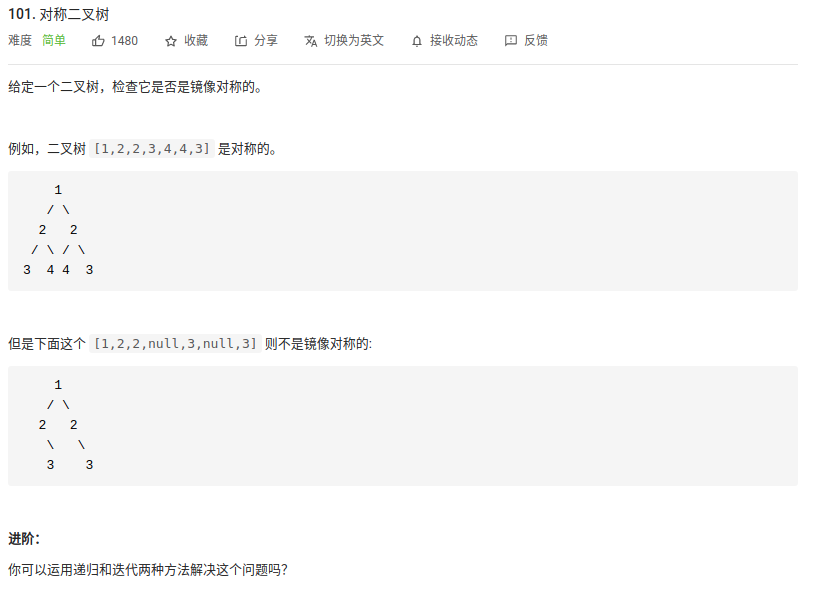
先来想一下如果我们要人工的判断一棵树是否是对称的，我们会怎么做？
肯定是首先判断根节点的左子树是否等于根节点的右子树，
然后如果相等再判断左子树的左子树是否等于右子树的右子树，
再判断左子树的右子树是否等于右子树的左子树。
递归：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return compare(root.left, root.right);
    }

    private boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        } 
        if (left == null || right == null) {
            return false;
        }
        if (left.val != right.val) {
            return false;
        }
        return compare(left.left, right.right) && compare(left.right, right.left);
    }
}

迭代：
利用两个镜像树进入队列，镜像树就是指两个一样的树，将u树的左儿子节点放入队列，就对应的将v树的右儿子节点放入队列；将u树的右儿子节点放入队列，就对应的将v树的左儿子节点放入队列。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Deque<TreeNode> queue = new LinkedList<>();
        TreeNode u = root;
        TreeNode v = root;
        queue.offer(u);
        queue.offer(v);
        while (!queue.isEmpty()) {
            u = queue.poll();
            v = queue.poll();
            if (u == null && v == null) {
                continue;
            }
            if (u == null || v == null) {
                return false;
            }
            if (u.val != v.val) {
                return false;
            }
            queue.offer(u.left);
            queue.offer(v.right);

            queue.offer(u.right);
            queue.offer(v.left);
        }
        return true;
    }
}

2. “104. 二叉树的最大深度”

求二叉树的最大深度也就是求左子树和右子树的最大深度之间的最大值，也就是Math.max(left, right)+1，并且加上1是因为要算上自己的高度，比如说只有一个节点的二叉树，根节点为2，它的儿子节点都为空，那么左子树和右子树的最大深度的最大值为0，这颗树的高度也就是最大深度+自己的高度=1。
并且需要注意的是我们的从树底从树顶遍历，因为我们先得算出子树的高度。

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left, right) + 1;
    }
}

3. “111. 二叉树的最小深度”

求二叉数的最小深度就不能简单的套用Math.min(left, right) + 1了，因为考虑这一种情况，当二叉树是一颗歪脖子树时，也就是所有树的节点都在一边，也就是每个节点的左儿子都为空时，如果单纯套用Math.min(left, right) + 1，算出的答案肯定是1，这是因为每次Math.min都会去取左儿子为空的那个值。
因此我们需要考虑当父节点的左儿子或者右儿子为空的情况，如果一个节点的左儿子为空，那么以这个节点为根的二叉树的最小深度一定是它的右儿子的最小深度+1

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (root.left == null) {
            return right + 1;
        }
        if (root.right == null) {
            return left + 1;
        }
        return Math.min(left, right) + 1;
    }
}

4. “222. 完全二叉树的节点个数”

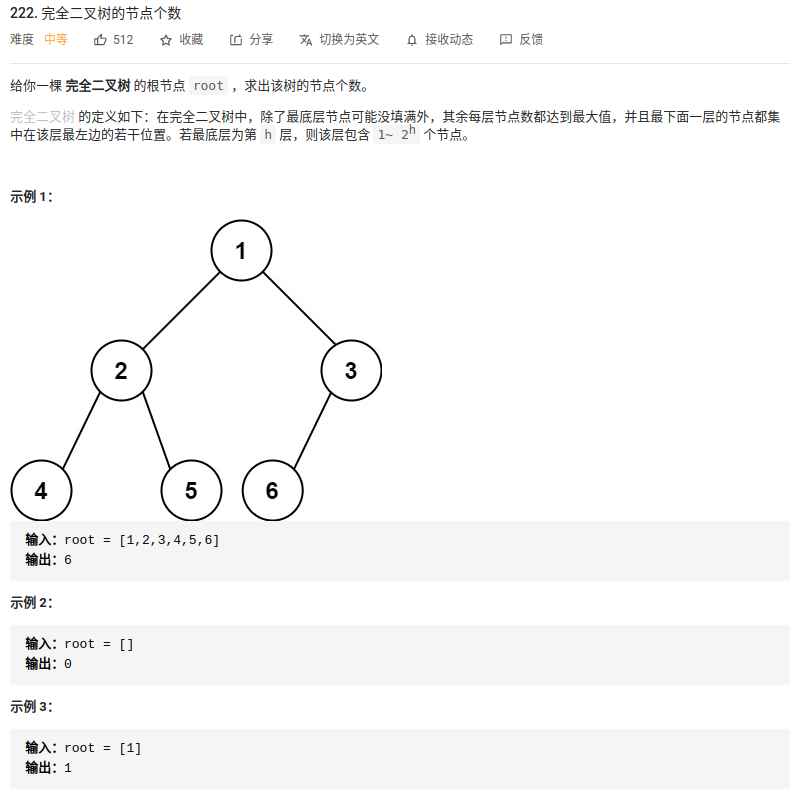
完全二叉树的特性是除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。
因此我们记录左子树的最左边的节点的深度，以及右子树的最左边节点的深度。
那么有这么几种情况：

左子树的最左边节点的深度等于右子树的最左边节点的深度
那么代表这颗完全二叉树的左子树是满的，直接根据左子树深度计算出节点树即可。
而右子树不一定是满的，继续去右子树中寻找。
左子树的最左边节点的深度大于右子树的最左边节点的深度
代表二叉树中最底层节点右子树的那块位置一定是一个节点都没有的，因此直接用右子树的最左边节点的深度计算出除最底层节点之外的节点数，然后去左子树中寻找

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        if (leftHeight == rightHeight) {
            return countNodes(root.right) + (1 << leftHeight);
        } else {
            return countNodes(root.left) + (1 << rightHeight);
        }
    }

    private int getHeight(TreeNode root) {
        int height = 0;
        while (root != null) {
            height++;
            root = root.left;
        }
        return height;
    }
}

5. “110. 平衡二叉树”

首先分析题目，高度平衡的二叉树的要求是一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
我们就可以按照题目的要求，检查两颗子树之间的高度差是否大于1。
利用后序遍历，从树底到树顶进行检查，如果子树间的高度差大于1，则返回-1，如果不大于1，说明这颗树符合要求，返回两颗子树的深度的最大值，为什么要返回最大值呢？最小值不行吗？
因为我们计算子树的高度差是否大于1肯定是拿左子树的最大深度-右子树的最大深度，不可能是拿最小深度去计算的

class Solution {

    public boolean isBalanced(TreeNode root) {
        return depth(root) == -1 ? false : true;
    }

    private int depth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = depth(root.left);
        int right = depth(root.right);
        if (left == -1 || right == -1) {
            return -1;
        }
        return Math.abs(left - right) > 1 ? -1 : Math.max(left, right) + 1;
    }
}

6. “257. 二叉树的所有路径”

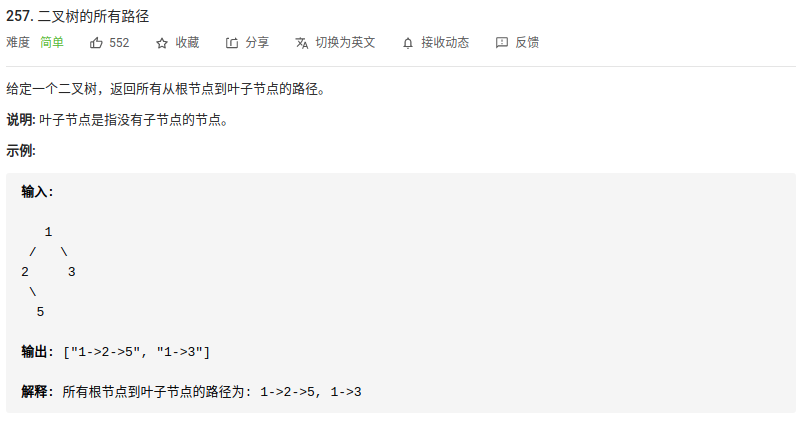
这题使用回溯加上dfs的方式，使用前序遍历。
当未遍历到叶子节点时，将节点放入到path中，
当遍历到叶子节点时，也就是root.left == null && root.right == null时，path中就是从根节点到叶子节点的完整路径。

class Solution {

    private List<String> path = new ArrayList<>(); 
    private StringBuilder pathString = new StringBuilder();
    private List<String> ans = new ArrayList<>();
    
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root);
        return ans;
    }

    private void dfs(TreeNode root) {
        path.add(String.valueOf(root.val));
        if (root.left == null && root.right == null) {
            for (int i = 0; i < path.size() - 1; i++) {
                pathString.append(path.get(i) + "->");
            }
            pathString.append(path.get(path.size() - 1));
            ans.add(pathString.toString());
            pathString.setLength(0);
            return;
        }
        if (root.left != null) {
            dfs(root.left);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            dfs(root.right);
            path.remove(path.size() - 1);
        }
    }
}

7. “404. 左叶子之和”

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。
因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：如果左节点不为空，且左节点没有左右孩子，那么这个节点就是左叶子
当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和右子树左叶子之和，相加便是整个树的左叶子之和。
递归：

class Solution {
   public int sumOfLeftLeaves(TreeNode root) {
      return dfs(root);
   }

   private int dfs(TreeNode root) {
      if (root == null) {
         return 0;
      }
      int left = dfs(root.left);
      int right = dfs(root.right);
      if (root.left != null && root.left.left == null && root.left.right == null) {
         return root.left.val + left + right;
      }
      return left + right;
   }
}

迭代：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        int ans = 0;
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode cur = stack.pop();
            if (cur.left != null && cur.left.left == null && cur.left.right == null) {
                ans += cur.left.val;
            }
            if (cur.left != null) {
                stack.push(cur.left);
            }
            if (cur.right != null) {
                stack.push(cur.right);
            }
        }
        return ans;
    }

}

8. “513. 找树左下角的值”

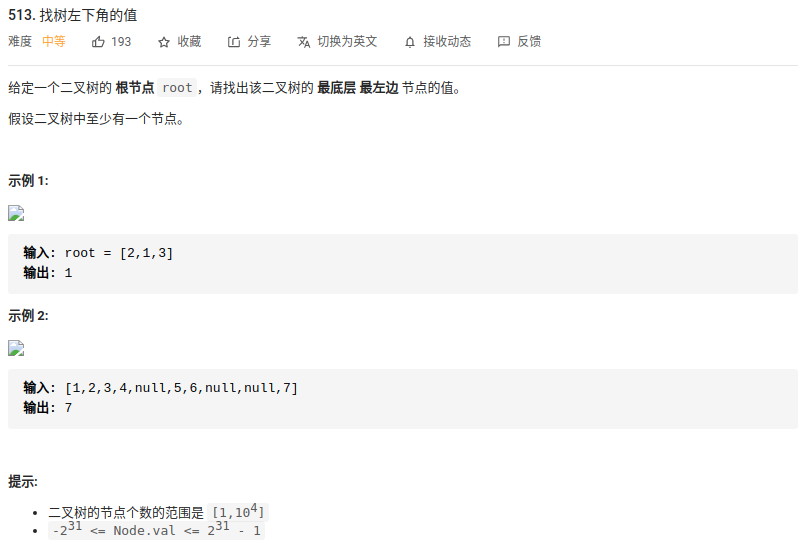
层序遍历：
本题要求是找到二叉树中最底层最左边节点的值，看到这个要求第一个想到的就是用层序遍历，因为层序遍历是一层一层向下遍历，并且是从左到右进行的，因此每当遍历到每一层的第一个节点时，就记录这个值。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        int ans = 0;
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int n = queue.size();
            for (int i = 0; i < n; i++) {
                TreeNode cur = queue.poll();
                if (i == 0) {
                    ans = cur.val; 
                }
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
        }
        return ans;
    }
}

递归：
找到二叉树中最底层最左边的节点有两个条件：

最底层代表了该节点的深度最大
最左边代表可以使用前序遍历，当第一次找到符合条件的节点就代表这个节点就是符合条件的

因此我们先计算出这个二叉树的最大深度，然后使用前序遍历，当第一次找到符合条件的节点就代表找到了答案，使用flag让之后的递归直接返回。
并且这个条件就是节点的深度等于二叉树的最大深度以及节点的儿子节点都为空，我们使用回溯来记录节点的深度。

class Solution {
    
    private int ans = 0;
    private int k = 0;
    private boolean flag = false;
    
    public int findBottomLeftValue(TreeNode root) {
        int depth = depth(root);
        dfs(root, depth);
        return ans;
    }
    
    private void dfs(TreeNode root, int depth) {
        if (root == null || flag == true) {
            return;
        }
        k++;
        if (root.left == null && root.right == null && k == depth) {
            ans = root.val;
            flag = true;
            return;
        }
        if (root.left != null) {
            dfs(root.left, depth);
            k--;
        }
        if (root.right != null) {
            dfs(root.right, depth);
            k--;
        }
    }
    
    private int depth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = depth(root.left);
        int right = depth(root.right);
        return Math.max(left, right) + 1;
    }
}

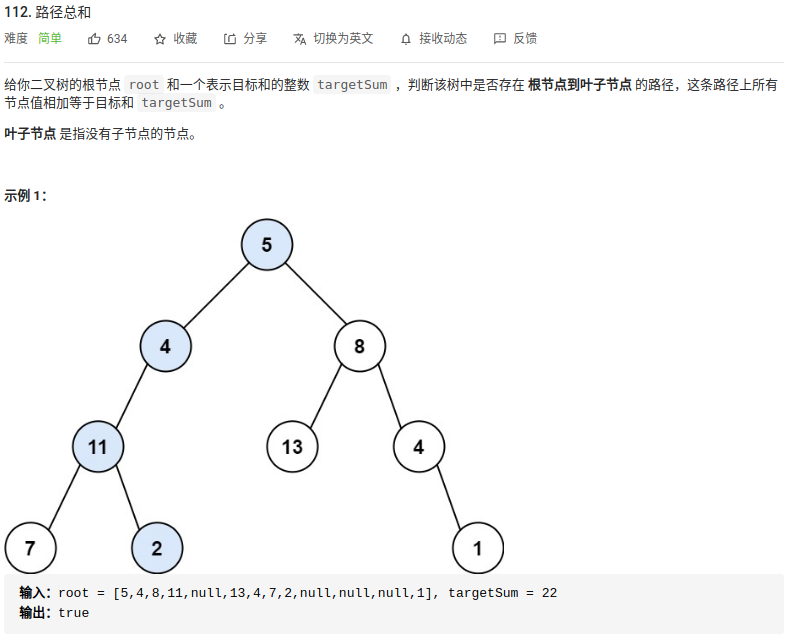
9. “112. 路径总和”

递归：
前序遍历，遍历时targetSum减去节点的值，判断target值是否等于0，当等于0并且节点的儿子节点都为空时代表找到了路径总和等于targetSum的叶子节点。
其实这题的target是用到回溯的，但是我们并没有写remove(),这是因为递归中传入了target，这样每次递归返回时是相当于用到旧值的

class Solution {
    
    private boolean ans = false;
    
    public boolean hasPathSum(TreeNode root, int targetSum) {
        dfs(root, targetSum);
        return ans;
    }

    private void dfs(TreeNode root, int target) {
        if (root == null) {
            return;
        }
        target -= root.val;
        if (target == 0 && root.left == null && root.right == null) {
            ans = true;
        }
        dfs(root.left, target);
        dfs(root.right, target);
    }
}