题目解析
方法一 暴力递归求解
这种方法其实就是使用递归的思想来求解,将每个数看成是一颗二叉树的节点,当且仅当找到二叉树的叶子节点(两个初始值0和1)时才结束循环,也就是递归的终止条件。画图说明,如下:
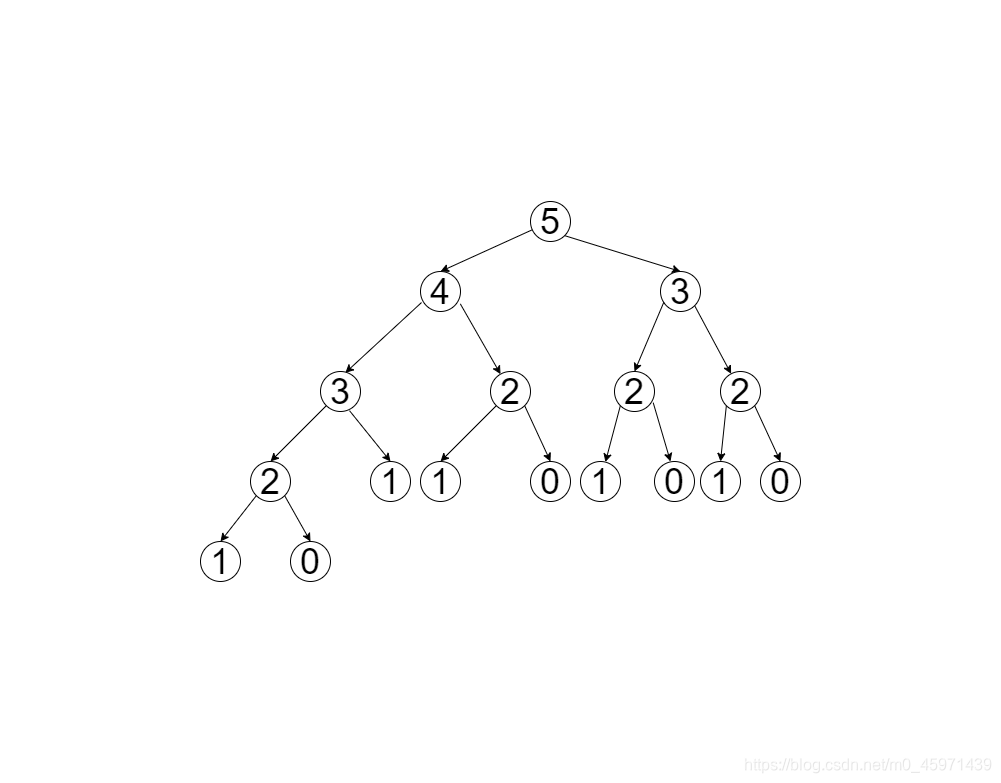
可以看出计算第n个节点的斐波那契数,即需要计算出整个二叉树每个节点的值,时间复杂度为2的n次方,非常庞大,代码见下。
方法二 暴力递归的优化
暴力递归求解中的时间复杂度如何去降低呢?可以发现,暴力递归需要计算上图中的每个二叉数节点的值,但是其中有一些值的计算是可以去除的,就是说存在大量的节点值的计算是冗余的。不难看出,当计算根节点时,需要计算节点4和节点3的值,但是计算节点4的值又需要计算节点3和节点2的值,如果左子树的值计算完毕,那么右子树的值就不要再去递归求解了,因此只需要计算图中的最长一条路径左中的节点的值,根节点的值自然可以求出。如下图,只需要计算红色路径上的值即可:
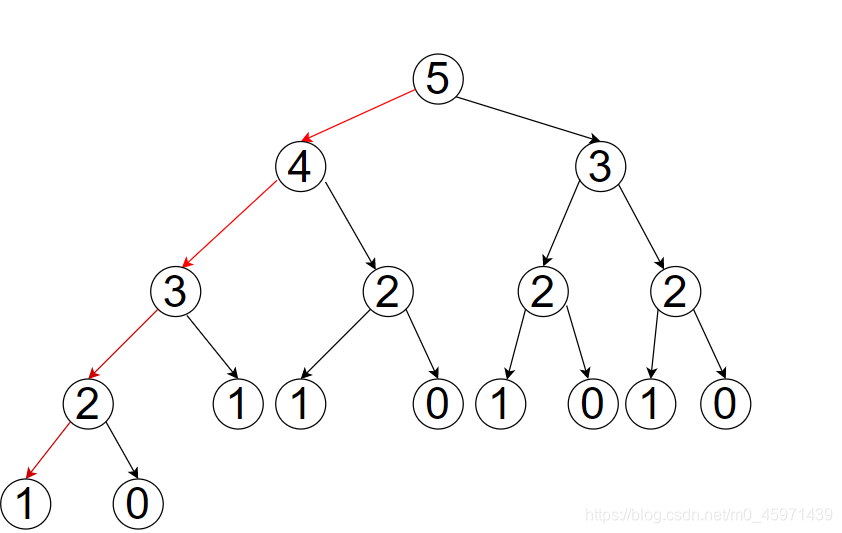
依次思路,只需要计算n个斐波那契数,时间复杂度可降低为O(n);
但是如何去得到每个节点的值呢?需要使用一个数组,来保存每次计算的节点值,最多只有n个值,那么空间复杂度为O(n)。
方法三 双指针思想
虽然方法二中去重递归可以将时间复杂度降低为O(n), 但是空间复杂度也为O(n),如何去降低这个空间复杂度呢?逐步求解某一个位置的元素值,并且是由某两个值来得到的,类似这种问题,都可以联想到双指针思想:
慢指针指向数组最左端,快指针指向数组下标为1的位置,逐步更新两个指针所指向的元素,直至遍历到第n个元素为止,即可得到第n个斐波那契数,此时的时间复杂度不变还是O(n),而空间上只有两个指针,并没有使用额外的空间,因此空间复杂度为O(1)。
代码解析
1. 暴力递归
public static int Fib1(int num) {
if (num == 0) {
return 0;
}
if (num == 1) {
return 1;
} else {
return Fib1(num - 1) + Fib1(num - 2);
}
}
2. 去重递归
public static int Fib2(int num) {
int[] arr = new int[num + 1]; //初始化全为0的整型数组,用来保存每次计算得到的Fib数值,避免重复计算
return resurse(arr, num);
}
private static int resurse(int[] arr, int nums) {
if (nums == 0) {
return 0;
}
if (nums == 1) {
return 1;
}
if (arr[nums] != 0) { //如果该Fib数不为0表示之前已经计算过该值了,直接进行返回,对于第一次才计算的值才使用递归求解
return arr[nums];
}
arr[nums] = resurse(arr, nums - 1) + resurse(arr, nums - 2);
return arr[nums];
}
注意:这里的arr数组初始化为全0的整数数组,因为后面当第一次计算某个斐波那契数时才需要进行递归求解,否则,当某个斐波那契数被计算得到了,此时已经存在数组arr的某个位置处,这个元素就不再是0了。当下一次再使用该值时,就不要再一次进行计算,直接返回该值即可。
3. 双指针求解
public static int Fib3(int num) {
int low = 0, high = 1;
if (num == 0) {
return 0;
}
if (num == 1) {
return 1;
}
for (int i = 2; i <= num; i++) {
int sum = low + high;
low = high;
high = sum;
}
return high;
}
定义两个指针:慢指针指向数组下标0,快指针指向数组下标1,同上设定两个default也就是两个斐波那契的初始值。从下标位置2开始循环,将上一次的元素进行加和得到当前的斐波那契数sum,更新两个指针:快指针所指向的值赋值给慢指针low,当前得到的斐波那契数sum赋值给快指针high,进行下一次求解,直至循环到第num个元素结束。最后直接返回快指针high即可,low指针保存的是上一个斐波那契数。