介绍

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。
顶点：图可以有零个或者多个元素（节点）
边：每个相邻元素之间被称为边或者圆弧，
定义：图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
如果任意两个顶点之间都存在边叫完全图，有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图。在用数学方式表示时，无向边用()表示，有向边用<>表示。

gitee: https://gitee.com/baichen9187/data-structure-and-algorithm
无向图
图形中所有边都无向的，这个图就是无向图
在这里插入图片描述

G1?={V1?,E2}?
v1 = {a,b,c,d,e}
e = {(a,b),(a,c),(a,d),(a,e),(b,c)…}
有向图
同时一个有方向的图称为有向图，所有边都是有向的

在这里插入图片描述

G1?={V1?,E2}?
v1 = {a,b,c,d,e}
e = {<a,b>,<a,c>,<b,d>,<c,e>,<d,e>,<d,a>}
顶点v的入度和出入，分别表示indeg(v),outdeg(v)
这里的顶点a，入度为1，出度为2
混合图
一个图中同时拥有有方向和无方向的边，称为混合图
在这里插入图片描述

由于边缘链接的两个顶点呗称为边的端点。如果边是有向的，他的第一个端点是起点，另一个是终点，如果u和v之间存在一条边，则称他们为相邻的，如果顶点是边的端点之一，侧这条边呗称为入射到这个顶点

图的抽象数据结构

图是顶点和边的结合，我们可以抽象为三种数据类型的组合，vertex顶点，edge边，greaph图，顶点是任意元素的对象，edge是存储关联的对象
图的数据结构
例图
在这里插入图片描述

边列表

边列表是图的一种存储结构，用来描述图上的每一个点。对图的每个边进行编号，对图的每个顶点建立一个双向链表（n个顶点建立n个链表），第i个容器中的结点包含以顶点Vi为起点的所有边的编号。

在这里插入图片描述
表现如下：

邻接列表

通过将图形的边存储到较小的为止来对其进学校分组，从而和每个单独的顶点相关的刺激容器集合起来，每个顶点v维持一个集合，该集合称为v的入射集合，其中全部都是入射到v的边。

邻接矩阵需要为每个顶点都分配n个边的空间,其实有很多边都是不存在,会造成空间的一定损失.
邻接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组+链表组成

在这里插入图片描述
表现如下：

在这里插入图片描述

邻接图

基于邻接列表来实现，我们使用哈希表为每个入射边的相反端点作为图的逐渐，用边结构作为值，相比邻接列表来说，可以快速通过顶点来快速搜索

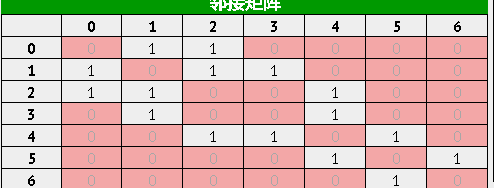
在这里插入图片描述

领结矩阵

领结矩阵是表示图形中顶点之间相邻关系的矩阵，对玉n个顶点的图而言，矩阵是row和col表示的1-n个点

在这里插入图片描述

图的遍历

深度优先遍历思想

深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点,可以这样理解:每次都在访间完当前结点后首先访问当前结点的第一个邻接结点。我们可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问，显然,深度优先搜索是一个 递归回溯问题的过程

深度优先遍历算法步骤

访问初始结点v,并标记结点v为已访问。
查找结点v的第一个邻接结点w.
若w存在,则继续执行4,如果w不存在,则回到第1步,将从v的下一个结点继续。
若w未被访问,对w进行深度优先遍历递归(即把w当做另一个v,然后进行步骤123)。
查找结点v的w邻接结点的下一个邻接结点,转到步骤3。

在这里插入图片描述

    public void dfs(){
        isVisited = new boolean[vertexList.size()]; //最大布尔数组
        for(int i = 0; i < vertexList.size(); i++) {
            if(!isVisited[i]) {
                dfs(isVisited, i);
            }
        }
    }

    public void dfs(boolean[] isVisited, int index){
        System.out.print(vertexList.get(index) + "->");
        isVisited[index] = true;
        int w = getFirstNeighbor(index);
        while(w != -1) {
            if(!isVisited[w]) {
                dfs(isVisited, w);
            }
            w = getNextNeighbor(index, w);
        }

    }

package com.dataSructure.graph;


import java.util.Random;

public class GraphDemo {

    public static void main(String[] args) {


        String[] Vertexs = {"1", "2", "3", "4", "5", "6", "7","8"};
        Random r = new Random();
        Graph graph = new Graph(Vertexs.length);

        for(String vertex: Vertexs) {
            graph.insertVertex(vertex);
        }

//        for(int i = 0;Vertexs.length > i;i++){
//                graph.insertEdge(i, r.nextInt(Vertexs.length));
//        }
        graph.insertEdge(0, 2);
        graph.insertEdge(0, 3);
        graph.insertEdge(0, 5);
        graph.insertEdge(1, 6);
        graph.insertEdge(1, 7);
        graph.insertEdge(2, 0);
        graph.insertEdge(2, 6);
        graph.insertEdge(3,0 );
        graph.insertEdge(4, 3);
        graph.insertEdge(4, 5);
        graph.insertEdge(5, 0);
        graph.insertEdge(5, 7);
        graph.insertEdge(5, 4);
        graph.insertEdge(6, 1);
        graph.insertEdge(6, 2);
        graph.insertEdge(7, 1);
        graph.insertEdge(7, 5);
        graph.showGraph();
        graph.dfs(); // A->B->C->D->E [1->2->4->8->5->3->6-

在这里插入图片描述

图的广度优先搜索(Broad First Search)

bfs以回合的方式进行并且将顶点分成不同级别，以顶点开始，级别是0，在第一轮标记被访问过，对于所有和顶点相邻的顶点，级别为1，在第二轮，允许从开始顶点走两步，将这些新的顶点和级别1的顶点领近但没设置过级别的设置为2，并标记被访问过。反复如此

广度优先遍历算法步骤

访问初始结点v并标记结点v为已访问。
结点v入队列
当队列非空时,继续执行,否则算法结束。
出队列，取得队头结点u。
查找结点u的第一个邻接结点w.
若结点u的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
1. 若结点w尚未被访问,则访问结点w并标记为已访问。
2. 结点w入队列
3. 查找结点u的继w邻接结点后的下一个邻接结点w,转到步骤6.

在这里插入图片描述

private void bfs(boolean[] isVisited, int i) {
    int u;  
    int w; 

    LinkedList queue = new LinkedList();
    System.out.print(vertexList.get(i) + ">");
    isVisited[i] = true;
    queue.addLast(i);

    while (!queue.isEmpty()) {
        u = (Integer) queue.removeFirst();
        w = getFirstNeighbor(u);
        while (w != -1) {
            if (!isVisited[w]) {
                System.out.print(vertexList.get(w) + ">");
                isVisited[w] = true;
                queue.addLast(w);
            }
            w = getNextNeighbor(u, w);
        }
    }

}

public void bfs() {
    isVisited = new boolean[vertexList.size()];
    for (int i = 0; i < vertexList.size(); i++) {
        if (!isVisited[i]) {
            bfs(isVisited, i);
        }
    }
}