前言
前一阵子准备秋招,做了几家公司的笔试题。发现有关DP算法的题目很多,只不过那个时候我对动态规划思想还不是很了解。于是我下定决心,查找了相关的文献和资料准备彻底的理解DP算法。
DP算法核心思想
将大问题划分为小问题进行解决,从而一步步获取最优解;动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
dp与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 ),依次解决各子问题,最后一个子问题就是初始问题的解,而分治法各个子问题是相互独立的。
DP算法作用
1. 计数
- 有多少种方式走到右下角
- 有多少种方式选出K个数使得和为sum
2. 求最大(小)值
- 求从左上角走到右下角路径的最大数字和
- 求最长上升子序列的长度
3. 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和为sum
DP算法解题步骤
1. 确定状态
2. 确定转移方程
3. 确定开始和边界条件
4. 计算顺序
计数型
机器人路径规划
场景引入:
一个机器人只能向下和向右移动,每次只能移动一步,设计一个算法求机器人
从(1,1)到(m,n)有多少条路径。
确定状态
1.1"最后一步"
无论机器人如何到达右下角,始终会走到如下图所示的两个位置;
假设机器人右下角所在位置的下标为(m-1,n-1)
那么机器人上一步的位置的下标一定是(m-2,n-1)或者(m-1,n-2)

1.2"化解子问题"
设机器人有x种方法走到(m-2,n-1),有y种方法走到(m-1,n-2)
(1)机器人从左上角走到(m-1,n-1)共x+y中走法
(2)问题就转化为从左上角有多少种走法到(m-2,n-1)和(m-1,n-2)
(3)状态:设f(i,j)为机器人从左上角走到(i,j)
确定转移方程
对于任意一个格子有:
f[i][j] = f[i-1][j]+f[i][j-1]
确定开始和边界条件
初始条件:f[0][0]=1
边界条件:i=0或者j=0的时候就只有可能从一个地方过来,此时f[i][j]=1
计算顺序
从初始条件f[0][0]=1开始计算
计算第0行:f[0][0],f[0,1],...,f[0,n-1]
计算第1行:f[1,0],f[1,1],...,f[1,n-1]
...
计算m-1行:f[m-1][0],f[m-1,1],...[f[m-1][n-1]
代码实现
代码如下:
public class DP {
public static int walkWays(int m,int n){
//判断参数的合法性
if (m == 0 || n == 0){
return 0;
}
//初始化dp数组
int[][] dp = new int[m][n];
for (int row = 0; row < m; row++) {
for (int col = 0; col < n; col++) {
//临界条件
if (row == 0 || col == 0){
dp[row][col] = 1;
}else {
dp[row][col] = dp[row-1][col] + dp[row][col-1];
}
}
}
return dp[m-1][n-1];
}
public static void main(String[] args) {
System.out.println(walkWays(3, 3));
}
}
求最值
兑换零钱
场景引入:
一道非常经典的题,假设硬币有2元,5元和7元,每种硬币都足够多。买一支钢笔需要
花费27元。求如何使用硬币可以使得硬币的数量最少且商家不用找钱给消费者?
确定状态
1.1"最后一步"
假设最后一枚硬币面值为ak,那么前面硬币的面值肯定为27-ak
(1)虽然我们不知道最优策略是什么,但是最优策略肯定是a1,a2,...,ak面值加起来
是为27
(2)最后一枚硬币的面值一定是ak
(3)除掉最后一枚硬币,其余所有硬币面值之和为27-ak

注意:
(1)我们不关心前k-1枚硬币是如何拼出27-ak(因ak的值不确定,所以有很多种可能)
(2)由于是策略最优,所以27-ak的硬币数量是最少的
1.2"化解子问题"
原问题:最少用多少枚硬币拼出27
子问题:最少用多少枚硬币拼出27-ak
为了简化定义,设状态为f(x)=最少用多少枚硬币拼出x
由于ak没有确定,因此ak可以是2,5,7中任意一枚硬币的面值
(1)若ak=2,则f(27)=f(27-2)+1(1表示最后一枚面值为2的硬币)
(2)若ak=5,则f(27)=f(27-5)+1(1表示最后一枚面值为5的硬币)
(3)若ak=7,则f(27)=f(27-7)+1(1表示最后一枚面值为7的硬币)
确定转移方程
由第一步的分析,可以得出转移方程:
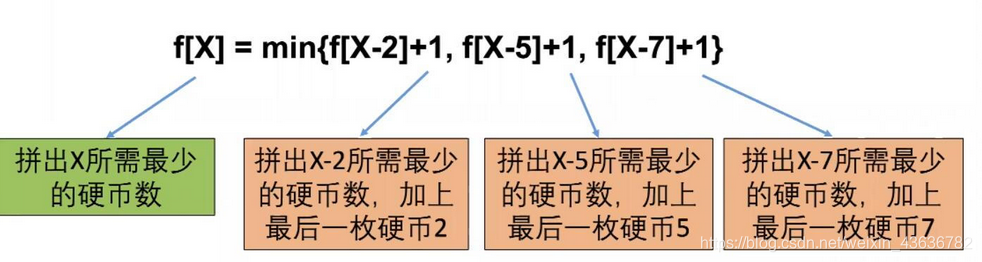
确定开始和边界条件
初始条件:f[0] = 0;
边界条件:
(1)x-2或者x-5或者x-7小于0
(2)如果拼不出给定的值,那么最终f[x]就趋于无穷大
计算顺序
从初始条件f[0]=0开始计算,求f(1),f(2),...,f(27)
代码实现
代码如下:
import java.util.Arrays;
public class DP {
public static int minCoinNums(int[] coins,int money){
//判断参数的合法性
if (coins.length == 0 || coins == null || money <= 0){
return -1;
}
//初始化dp数组
int[] dp = new int[money+1];
//初始化金额为i的硬币数
Arrays.fill(dp,money+1);
//初始化初始条件
dp[0] = 0;
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < coins.length; j++) {
//金额数大于等于硬币的面值,就求当前金额所需要的最小硬币个数
if (i >= coins[j]){
dp[i] = Math.min(dp[i],dp[i-coins[j]]+1);
}
}
}
return dp[money] > money ? -1 : dp[money];
}
public static void main(String[] args) {
int[] coins = {2,5,7};
System.out.println(minCoinNums(coins, 27));
}
}