[数据结构与算法]数据结构与算法学习笔记（六）栈的快速入门及使用栈实现逆波兰表达式求解

0x01 栈

• 定义：栈（stack）是一个有序线性表，只能在表的一端（称为栈顶，top）执行插入和删除操作。最后插入的元素将第一个被删除。所以，栈也称为后进先出（Last In First Out，LIFO）或先进后出（First In Last Out，FILO）线性表。栈的局限性就是栈的最大空间必须先声明且不能改变。
• 两个专有操作：
  – 入栈 (push)：表示在栈中插入一个元素；
  – 出栈 (pop)：表示从栈中删除一个元素；
  试图对一个空栈执行出栈操作称为下溢（underflow）；试图对一个满栈执行入栈操作称为溢出（overflow）。
• 栈的常用操作
  – void push(int data)：将data（数据）插入栈；
  – int pop()：删除并返回最后一个插入栈的元素；
  – int top()：返回最后一个插入栈的元素，但不删除；
  – int size()：返回存储在栈中元素的个数；
  – boolean isEmpty()：判断栈中是否有元素；
  – boolean isFull()：判断栈中是否存满元素。
• 栈的应用
  直接应用
  – 符号匹配
  – 中缀表达式转换为后缀表达式
  – 计算后缀表达式
  – 实现函数调用（包括递归）
  – 求范围误差（极差）
  – 网页浏览器中历史记录
  – 文本编辑器的撤销（undo）序列
  – HTML和XML文件中的标签（tag）匹配
  间接应用
  – 作为一个算法的辅助数据结构（如，树遍历算法）
  – 其他数据结构的组件
• 栈的常用实现方式
  – 基于简单数组的实现
  – 基于动态数组的实现
  – 基于链表的实现
• 入门简单实现

package com.atCodeSun.stack06;

import java.util.Scanner;

/**
 * @author codeSun
 * @create 2021-08-07 16:48
 */
public class ArrayStackDemo {

    public static void main(String[] args) {
        //测试ArrayStack是否正确
        //先创建一个ArrayStack对象，表示栈
        ArrayStack stack = new ArrayStack(4);
        String key = "";
        boolean loop = true; //控制是否退出菜单
        Scanner scanner = new Scanner(System.in);

        while(loop) {
            System.out.println("show：表示显示栈");
            System.out.println("exit：退出程序");
            System.out.println("push：表示添加数据到栈（入栈）");
            System.out.println("pop：表示从栈取出数据（出栈）");
            System.out.println("请输入你的选择");
            key = scanner.next();
            switch (key){
                case "show":
                    stack.list();
                    break;
                case "push":
                    System.out.println("请输入一个数");
                    int value = scanner.nextInt();
                    stack.push(value);
                    break;
                case "pop":
                    try {
                        int res = stack.pop();
                        System.out.printf("出栈的数据是%d\n",res);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;
                case "exit":
                    scanner.close();
                    loop = false;
                default:
                    break;
            }
        }
        System.out.println("程序退出了");
    }

}





//定义一个ArrayStack表示栈
class ArrayStack{
    private int maxSize; //栈的大小
    private int[] stack; //数组，数组模拟栈，数据就放在该数组
    private int top = -1; //top表示栈顶，初始化为-1


    //构造器
    public ArrayStack(int maxSize){
        this.maxSize = maxSize;
        stack = new int[this.maxSize];
    }


    //栈满
    public boolean isFull(){
        return top == maxSize -1;
    }


    //栈空
    public boolean isEmpty(){
        return top == -1;
    }


    //入栈 push
    public void push(int value){
        //先判断栈是否满
        if(isFull()){
            System.out.println("栈满");
            return;
        }
        top++;
        stack[top] = value;
    }


    //出栈 pop 将栈顶的数据返回
    public int pop(){
        //先判断栈是否空
        if(isEmpty()){
            //抛出异常
            throw new RuntimeException("栈空，没有数据~");
        }
        int value = stack[top];
        top--;
        return value;
    }


    //遍历栈 遍历时需要从栈顶开始显示数据
    public void list(){
        if(isEmpty()){
            System.out.println("栈空，没有数据~");
            return;
        }
        //从栈顶开始显示数据
        for(int i = top; i >= 0; i--){
            System.out.printf("stack[%d]=%d\n",i,stack[i]);
        }
    }
}

0x02 中缀、前缀和后缀表达式

• 中缀表达式
  ??是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间（例：3 + 4），中缀表达式是人们常用的算术表示方法。与前缀或后缀记法不同的是，中缀记法中括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来，用于指示运算的次序。
• 前缀表达式（波兰式）
  ??前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。为纪念其发明者波兰数学家Jan Lukasiewicz，前缀表达式也称为“波兰式”。例如，- 1 + 2 3，它等价于1-(2+3)。
  – 运算优势
  ??前缀表达式是一种十分有用的表达式，将中缀表达式转换为前缀表达式后，就可以只依靠出栈、入栈两种简单操作完全解决中缀表达式的全部运算。
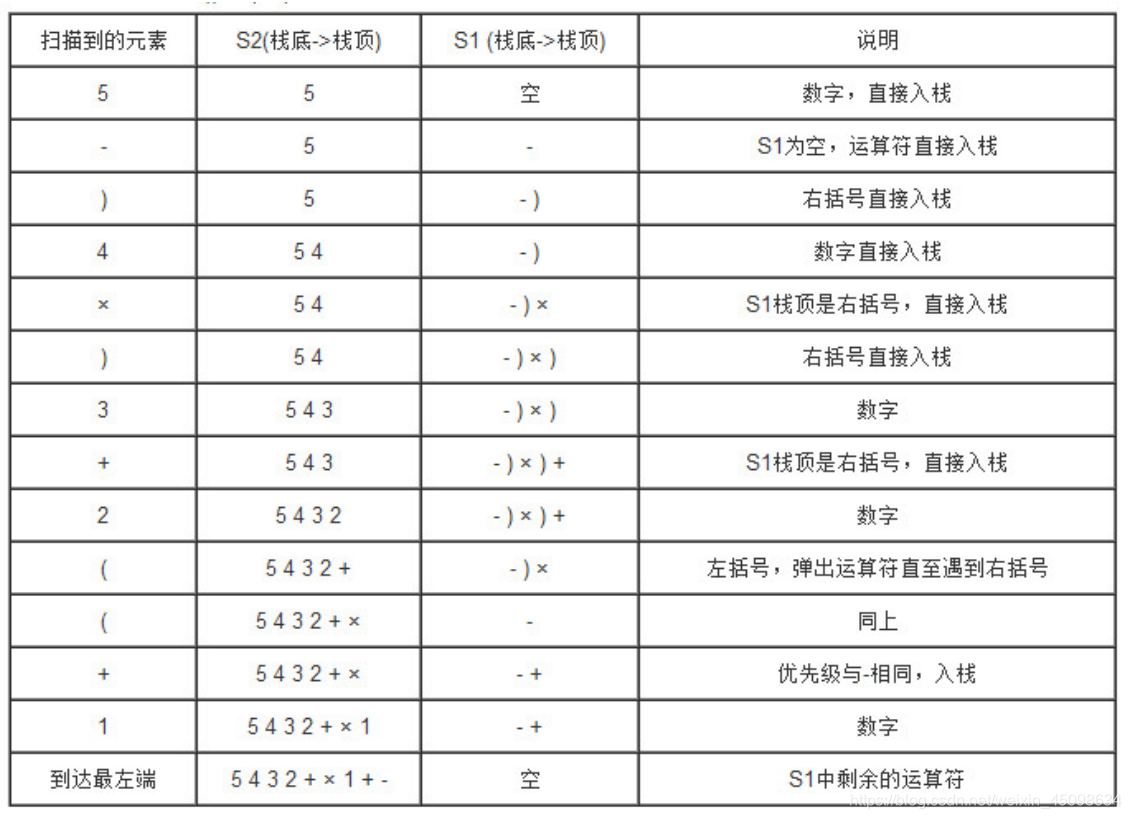
  – 中缀表达式转换为前缀表达式中缀转前缀方法摘自此博文
  例如：
  1+((2+3)×4)-5
  遵循以下步骤：
  (1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
  (2) 从右至左扫描中缀表达式；
  (3) 遇到操作数时，将其压入S2；
  (4) 遇到运算符时，比较其与S1栈顶运算符的优先级：
  (4-1) 如果S1为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈；
  (4-2) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1；
  (4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
  (5) 遇到括号时：
  (5-1) 如果是右括号“)”，则直接压入S1；
  (5-2) 如果是左括号“(”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到右括号为止，此时将这一对括号丢弃；
  (6) 重复步骤(2)至(5)，直到表达式的最左边；
  (7) 将S1中剩余的运算符依次弹出并压入S2；
  (8) 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。
  
  – 求值方法
  ??对前缀表达式求值，要从右至左扫描表达式，首先从右边第一个字符开始判断，若当前字符是数字则一直到数字串的末尾再记录下来，若为运算符，则将右边离得最近的两个“数字串”作相应运算，然后以此作为一个新的“数字串”并记录下来；扫描到表达式最左端时扫描结束，最后运算的值即为表达式的值。
  例如：对前缀表达式“- 1 + 2 3”求值，扫描到3时，记录下这个数字串，扫描到2时，记录下这个数字串，当扫描到+时，将+右移做相邻两数字串的运算符，记为2+3，结果为5，记录下5这个新数字串，然后继续向左扫描，扫描到1时，记录下这个数字串，扫描到-时，将-右移做相邻两数字串的运算符，记为1-5，结果为-4，此时关于这个表达式的全部运算已完成，故表达式的值为-4。
• 后缀表达式（逆波兰表达式）
  ??逆波兰式（Reverse Polish notation，RPN，或逆波兰记法），也叫后缀表达式（将运算符写在操作数之后）
  – 中缀表达式转换为后缀表达式中缀转前缀方法摘自此博文
  1+((2+3)×4)-5
  遵循以下步骤：
  (1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
  (2) 从左至右扫描中缀表达式；
  (3) 遇到操作数时，将其压入S2；
  (4) 遇到运算符时，比较其与S1栈顶运算符的优先级：
  (4-1) 如果S1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
  (4-2) 否则，若优先级比栈顶运算符高，也将运算符压入S1（注意转换为前缀表达式时是优先级较高或相同，而这里则不包括相同的情况）；
  (4-3) 否则，比栈顶低或相同，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
  (5) 遇到括号时：
  (5-1) 如果是左括号“(”，则直接压入S1；
  (5-2) 如果是右括号“)”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到左括号为止，此时将这一对括号丢弃；可以想象成“（”比任何运算符都高，“）”比任何运算符都低 。
  (6) 重复步骤(2)至(5)，直到表达式的最右边；
  (7) 将S1中剩余的运算符依次弹出并压入S2；
  (8) 依次弹出S2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式（转换为前缀表达式时不用逆序）。
  
  – 求值方法
  ??从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

0x03 使用栈实现逆波兰表达式求解代码

package com.atCodeSun.stack06;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

/**
 * @author codeSun
 * @create 2021-08-08 19:18
 */
public class PolandNotation {

    public static void main(String[] args) {


        //完成将一个中缀表达式转换成后缀表达式的功能
        //1+((2+3)*4)-5
        //说明：直接对str操作不方便，因此先将1+((2+3)*4)-5存放成对应的list 即1+((2+3)*4)-5 ----> ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
        String expression = "1+((2+3)*4)-5";
        List<String> infixExpressionList = toInfixExpressionList(expression);
        System.out.println("中缀表达式对应的List" + infixExpressionList);

        //将得到的中缀表达式对应的list转换成后缀表达式对应的list 即ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] ----> 即ArrayList [1,2,3,+,4,*,+,5,-]
        List<String> suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
        System.out.println("后缀表达式对应的List" + suffixExpressionList);

        //再计算出表达式的结果
        System.out.printf("expression=%d",calculate(suffixExpressionList));


    }



    //定义一个方法，中缀表达式转成对应的list存放
    public static List<String> toInfixExpressionList(String s){
        //定义一个list,存放中缀表达式的内容
        List<String> ls = new ArrayList<String>();
        int i = 0; //一个指针，用于遍历中缀表达式字符串
        String str; //对多位数的拼接
        char c; //每遍历一个字符，就放入到c
        do{
            //如果c是一个非数字，加入到ls
            if((c = s.charAt(i)) < 48 || (c = s.charAt(i)) < 57){
                ls.add("" + c); //转成字符串
                i++; //后移
            }else{ //如果是一个数，需要考虑多位数
                str = ""; //先将str置成""
                while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57){
                    str += c; //拼接
                    i++;
                }
                ls.add(str);
            }
        }while(i < s.length());
        return ls;
    }



    //方法：将得到的中缀表达式对应的list转换成后缀表达式对应的list
    public static List<String> parseSuffixExpressionList(List<String> ls){
        //定义两个栈
        Stack<String> s1 = new Stack<String>(); //符号栈
        //说明：因为s2这个栈在整个转换过程中，没有pop操作，而且后面还需要逆序输出，因此可直接使用List<String> s2
        List<String> s2 = new ArrayList<>(); //存放中间结果的list2
        //遍历ls
        for(String item: ls){
            //如果是一个数，加入s2
            if(item.matches("\\d+")){ //正则表达式匹配多位数
                s2.add(item);
            }else if(item.equals("(")){
                s1.push(item);
            }else if(item.equals(")")){
                //如果是右括号“）”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将一对括号丢弃
                while(!s1.peek().equals("(")){
                    s2.add(s1.pop());
                }
                s1.pop(); //消除小括号
            }else{
                //当item的优先级小于等于s1栈顶运算符，将s1栈顶的运算符弹出并加入到s2中，再次转到（4.1）与s1中的新的栈顶运算符相比较
                while(s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)){
                    s2.add(s1.pop());
                }
                //还需要将item压入栈
                s1.push(item);
            }
        }

        //将s1中剩余的运算符依次弹出并加入s2
        while(s1.size() != 0){
            s2.add(s1.pop());
        }

        return s2; //注意因为存放的是list，因此按顺序输出就是对应的后缀表达式
    }



    //完成对逆波兰表达式的运算
    /*
        从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，
        用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；
        重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。
     */
    public static int calculate(List<String> ls){
        //创建一个栈，只需要一个就可以
        Stack<String> stack = new Stack<>();
        //遍历ls
        for(String item: ls){
            //这里使用正则表达式取出数
            if(item.matches("\\d+")){ //匹配的是多位数
                //入栈
                stack.push(item);
            } else {
                //pop出两个数，并运算，结果再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if(item.equals("+")){
                    res = num1 + num2;
                } else if(item.equals("-")){
                    res = num1 - num2; //注意原表达式的运算法则
                } else if(item.equals("*")){
                    res = num1 * num2;
                } else if(item.equals("/")){
                    res = num1 / num2;
                } else{
                    throw new RuntimeException("运算符有误！！");
                }
                //把res入栈
                stack.push("" + res); //转成字符串
            }
        }
        //最后留在stack中的数据就是结果
        return Integer.parseInt(stack.pop());
    }

}


//编写一个类 Operation可以返回一个运算符 对应的优先级
class Operation{
    private static int ADD = 1;
    private static int SUB = 1;
    private static int MUL = 2;
    private static int DIV = 2;

    //写一个方法，返回对应的优先级数字
    public static int getValue(String operation){
        int result = 0;
        switch(operation){
            case "+":
                result = ADD;
                break;
            case "-":
                result = SUB;
                break;
            case "*":
                result = MUL;
                break;
            case "/":
                result = DIV;
                break;
            default:
                System.out.println("不存在该运算符！！");
                break;
        }
        return result;
    }
}