支持向量机通过得到
w
T
x
+
b
=
0
{w^T}x + b = 0
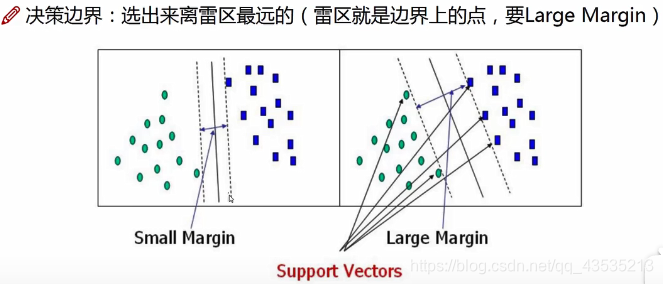
wTx+b=0划分超平面,来得到最优划分情况,即得到间隔最大的决策边界,而此时距离超平面(决策边界)最近的这几个样本点称之为支持向量(support vectors)。
数学公式:
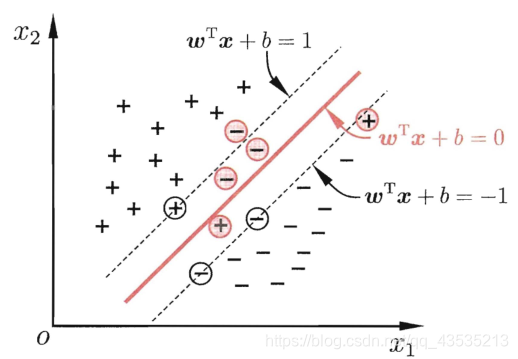
- 样本空间中任意点x到超平面的距离可写为 r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r = {{|{w^T}x + b|} \over {||w||}} r=∣∣w∣∣∣wTx+b∣?
- 假设超平面可将样本正确分类,则当 y i = + 1 , w T x i + b ≥ + 1 {y_i} = + 1,{w^T}{x_i} + b \ge + 1 yi?=+1,wTxi?+b≥+1;当 y i = ? 1 , w T x i + b ≤ + 1 {y_i} = - 1,{w^T}{x_i} + b \le + 1 yi?=?1,wTxi?+b≤+1。(已经过放缩变化,放缩前式子与0作比较)
- 对于支持向量而言,可使上述式子等号成立,两个异类支持向量到超平面的距离之和为(间隔) γ = 2 ∣ ∣ w ∣ ∣ \gamma = {2 \over {||w||}} γ=∣∣w∣∣2?。
- 故目标为 max ? w , b 2 ∣ ∣ w ∣ ∣ → min ? w , b 1 2 ∣ ∣ w ∣ ∣ 2 {\mathop {\max }\limits_{w,b} {2 \over {||w||}} \to \mathop {\min }\limits_{w,b} {1 \over 2}||w|{|^2}} w,bmax?∣∣w∣∣2?→w,bmin?21?∣∣w∣∣2 s . t . y i ( w T x i + b ) ≥ 1 s.t.{y_i}({w^T}{x_i} + b) \ge 1 s.t.yi?(wTxi?+b)≥1
- 利用拉格朗日乘子法求解,可将原本(d+1)个变量、n个约束,转变为n个变量、(n+1)个约束的求解问题。d为样本维度,n为样本数量,当进行非线性变化后,d会极大,故采用此方法简化求解。
拉格朗日乘子法:

从而可得到此问题的拉格朗日函数: L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m ( 1 ? y i ( w T x i + b ) ) L(w,b,\alpha ) = {1 \over 2}||w|{|^2} + \sum\limits_{i = 1}^m {(1 - } {y_i}({w^T}{x_i} + b)) L(w,b,α)=21?∣∣w∣∣2+i=1∑m?(1?yi?(wTxi?+b)) - 然后对上式w和b求偏导 w = ∑ i = 1 m α i y i x i w = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}} w=i=1∑m?αi?yi?xi? 0 = ∑ i = 1 m α i y i 0 = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}} 0=i=1∑m?αi?yi?
- 带入上式,将w和b消去,得到 max ? α ∑ i = 1 m α i ? ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \mathop {\max }\limits_\alpha \sum\limits_{i = 1}^m {{\alpha _i} - } \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T} } {x_j} αmax?i=1∑m?αi??i=1∑m?j=1∑m?αi?αj?yi?yj?xiT?xj? s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 s.t.\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,{\alpha _i} \ge 0 s.t.i=1∑m?αi?yi?=0,αi?≥0
- 上述过程需满足KKT条件:
α
i
≥
0
;
y
i
f
(
x
i
)
?
1
≥
0
;
α
i
y
i
f
(
x
i
)
?
1
=
0
{\alpha _i} \ge 0;{y_i}f({x_i}) - 1 \ge 0;{\alpha _i}{y_i}f({x_i}) - 1 = 0
αi?≥0;yi?f(xi?)?1≥0;αi?yi?f(xi?)?1=0
故对于任意训练样本都存在 α i = 0 {\alpha _i} = 0 αi?=0或者 y i f ( x i ) = 1 {y_i}f({x_i}) = 1 yi?f(xi?)=1。若 α i = 0 {\alpha _i} = 0 αi?=0,则该样本不在上式的求和中出现,也就不会对f(x)有任何影响;若 α i ≥ 0 {\alpha _i} \ge 0 αi?≥0,则必有 y i f ( x i ) = 1 {y_i}f({x_i}) = 1 yi?f(xi?)=1,所对应的样本点位于最大间隔边界上,是一个支持向量。
性质:训练完成后,大部分的训练样本都不保留,最终模型仅与支持向量有关。
核函数:
当原始样本空间内也许并不存在一个能正确划分两类样本的超平面,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。即
x
→
?
(
x
)
x \to \phi (x)
x→?(x),其对偶问题是:
max
?
α
∑
i
=
1
m
α
i
?
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
?
(
x
i
)
T
?
(
x
j
)
\mathop {\max }\limits_\alpha \sum\limits_{i = 1}^m {{\alpha _i} - } {1 \over 2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}\phi {{({x_i})}^T}} } \phi ({x_j})
αmax?i=1∑m?αi??21?i=1∑m?j=1∑m?αi?αj?yi?yj??(xi?)T?(xj?)
s
.
t
.
∑
i
=
1
m
α
i
y
i
=
0
,
α
i
≥
0
s.t.\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,{\alpha _i} \ge 0
s.t.i=1∑m?αi?yi?=0,αi?≥0
由于上式涉及到
?
(
x
i
)
T
?
(
x
j
)
\phi {({x_i})^T}\phi ({x_j})
?(xi?)T?(xj?),由于特征空间维数可能很高,甚至是无穷维,因此直接计算是困难的,可假设这样的函数
κ
(
x
i
,
x
j
)
=
<
?
(
x
i
)
,
?
(
x
j
)
>
=
?
(
x
i
)
T
?
(
x
j
)
\kappa ({x_i},{x_j}) = < \phi ({x_i}),\phi ({x_j}) > = \phi {({x_i})^T}\phi ({x_j})
κ(xi?,xj?)=<?(xi?),?(xj?)>=?(xi?)T?(xj?),即核函数。
常用的核函数:1.多项式核:
κ
(
x
i
,
x
j
)
=
(
x
i
T
x
j
)
d
\kappa ({x_i},{x_j}) = {(x_i^T{x_j})^d}
κ(xi?,xj?)=(xiT?xj?)d;2.高斯核:
κ
(
x
i
,
x
j
)
=
exp
?
(
?
∣
∣
x
i
?
x
j
∣
∣
2
2
σ
2
)
\kappa ({x_i},{x_j}) = \exp ( - {{||{x_i} - {x_j}|{|^2}} \over {2{\sigma ^2}}})
κ(xi?,xj?)=exp(?2σ2∣∣xi??xj?∣∣2?)
软间隔:
缓解过拟合问题的一个办法是允许支持向量机在一些样本上出错,引入“软间隔”,即允许某些样本不满足约束。
优化目标可写为:
min
?
w
,
b
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
m
l
0
/
1
(
y
i
(
w
T
x
i
+
b
)
?
1
)
\mathop {\min }\limits_{w,b} {1 \over 2}||w|{|^2} + C\sum\limits_{i = 1}^m {{l_{0/1}}({y_i}({w^T}{x_i} + b) - 1)}
w,bmin?21?∣∣w∣∣2+Ci=1∑m?l0/1?(yi?(wTxi?+b)?1),其中C>0,是个常数,
l
0
/
1
{l_{0/1}}
l0/1?是“0/1损失函数”。
然而此损失函数数学性质不好,使得式子不易求解,于是通常用其他函数来替代,称为“替代函数“,如下

引入松弛变量,可得到式子
min
?
w
,
b
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
m
ε
i
\mathop {\min }\limits_{w,b} {1 \over 2}||w|{|^2} + C\sum\limits_{i = 1}^m {{\varepsilon _i}}
w,bmin?21?∣∣w∣∣2+Ci=1∑m?εi?
s
.
t
.
y
i
(
w
T
x
i
+
b
)
≥
1
?
ε
i
;
ε
i
≥
0
s.t.{y_i}({w^T}{x_i} + b) \ge 1 - {\varepsilon _i};{\varepsilon _i} \ge 0
s.t.yi?(wTxi?+b)≥1?εi?;εi?≥0
可得下式拉格朗日函数
L
(
w
,
b
,
α
,
ε
,
μ
)
=
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
m
ε
i
+
∑
i
=
1
m
α
i
(
1
?
ε
i
?
y
i
(
w
T
x
i
+
b
)
)
?
∑
i
=
1
m
μ
i
ε
i
L(w,b,\alpha ,\varepsilon ,\mu ) = {1 \over 2}||w|{|^2} + C\sum\limits_{i = 1}^m {{\varepsilon _i}} + \sum\limits_{i = 1}^m {{\alpha _i}} (1 - {\varepsilon _i} - {y_i}({w^T}{x_i} + b)) - \sum\limits_{i = 1}^m {{\mu _i}{\varepsilon _i}}
L(w,b,α,ε,μ)=21?∣∣w∣∣2+Ci=1∑m?εi?+i=1∑m?αi?(1?εi??yi?(wTxi?+b))?i=1∑m?μi?εi?
对w,b和
ε
{\varepsilon }
ε求偏导可得
w
=
∑
i
=
1
m
α
i
y
i
x
i
{w = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{x_i}}}
w=i=1∑m?αi?yi?xi?、
0
=
∑
i
=
1
m
α
i
y
i
{0 = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}}}
0=i=1∑m?αi?yi?和
C
=
α
i
+
μ
i
{C = {\alpha _i} + {\mu _i}}
C=αi?+μi?,代入式中可得
max
?
α
∑
i
=
1
m
α
i
?
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\mathop {\max }\limits_\alpha \sum\limits_{i = 1}^m {{\alpha _i} - } \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}x_i^T} } {x_j}
αmax?i=1∑m?αi??i=1∑m?j=1∑m?αi?αj?yi?yj?xiT?xj?
s
.
t
.
∑
i
=
1
m
α
i
y
i
=
0
,
0
≤
α
i
≤
C
s.t.\sum\limits_{i = 1}^m {{\alpha _i}{y_i}} = 0,0 \le {\alpha _i} \le C
s.t.i=1∑m?αi?yi?=0,0≤αi?≤C
当C大的时候,意味着分类严格不能由错误;当C趋近于很小时,意味着可以有更大得错误容忍。
高斯核函数:
高斯核函数可将mn得数据映射为mm,其中m为数据量,n为数据特征。
其过程为,将m个数据依次与所有数据得相同特征计算相似度并加和,替代原有特征值
下图中变量m为数据特征数(与上述n一致),p为数据量(与上述m一致)

又因为高斯核函数可写为
exp
?
(
?
γ
∣
∣
x
i
?
x
j
∣
∣
2
)
{\exp ( - \gamma ||{x_i} - {x_j}|{|^2})}
exp(?γ∣∣xi??xj?∣∣2),当γ越大时,越容易过拟合,反之,偏向欠拟合。