逻辑回归由于存在易于实现、解释性好以及容易扩展等优点,被广泛应用于点击率预估(CTR)、计算广告(CA)以及推荐系统(RS)等任务中。逻辑回归虽然名字叫做回归,但实际上却是一种分类学习方法。
LR是一个传统的二分类模型,它也可以用于多分类任务,其基本思想是:将多分类任务拆分成若干个二分类任务,然后对每个二分类任务训练一个模型,最后将多个模型的结果进行集成以获得最终的分类结果。一般来说,可以采取的拆分策略有:
one vs all
LR实现简单高效易解释,计算速度快,易并行,在大规模数据情况下非常适用,更适合于应对数值型和标称型数据,主要适合解决线性可分的问题,但容易欠拟合,大多数情况下需要手动进行特征工程,构建组合特征,分类精度不高。
适用情景:LR是很多分类算法的基础组件,它的好处是输出值自然地落在0到1之间,并且有概率意义。因为它本质上是一个线性的分类器,所以处理不好特征之间相关的情况。虽然效果一般,却胜在模型清晰,背后的概率学经得住推敲。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。
应用上:
CTR预估,推荐系统的learning to rank,各种分类场景
某搜索引擎厂的广告CTR预估基线版是LR
某电商搜索排序基线版是LR
某新闻app排序基线版是LR
逻辑回归算法相信很多人都很熟悉,也算是我比较熟悉的算法之一了,毕业论文当时的项目就是用的这个算法。这个算法可能不想随机森林、SVM、神经网络、GBDT等分类算法那么复杂那么高深的样子,可是绝对不能小看这个算法,因为它有几个优点是那几个算法无法达到的,一是逻辑回归的算法已经比较成熟,预测较为准确;二是模型求出的系数易于理解,便于解释,不属于黑盒模型,尤其在银行业,80%的预测是使用逻辑回归;三是结果是概率值,可以做ranking model;四是训练快。当然它也有缺点,分类较多的y都不是很适用;对于自变量的多重共线性比较敏感,所以需要利用因子分析或聚类分析来选择代表性的自变量;另外预测结果呈现S型,两端概率变化小,中间概率变化大比较敏感,导致很多区间的变量的变化对目标概率的影响没有区分度,无法确定阈值。下面我先具体介绍下这个模型。
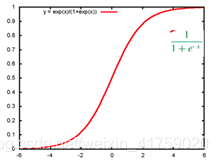
https://www.cnblogs.com/fionacai/p/5865480.html 可以结合这个来看,理解的更充分
GBDT
gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度,(此处是可以证明的)。
弱分类器一般会选择为CART TREE(也就是分类回归树)。由于上述高偏差和简单的要求 每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。
模型最终可以描述为:
其实说gbdt 能够构建特征并非很准确,gbdt 本身是不能产生特征的,但是我们可以利用gbdt去产生特征的组合。在CTR预估中,工业界一般会采用逻辑回归去进行处理,在我的上一篇博文当中已经说过,逻辑回归本身是适合处理线性可分的数据,如果我们想让逻辑回归处理非线性的数据,其中一种方式便是组合不同特征,增强逻辑回归对非线性分布的拟合能力。