[数据结构与算法]Algorithm第四版算法 C++实现(十四)——广度优先搜索（BFS）

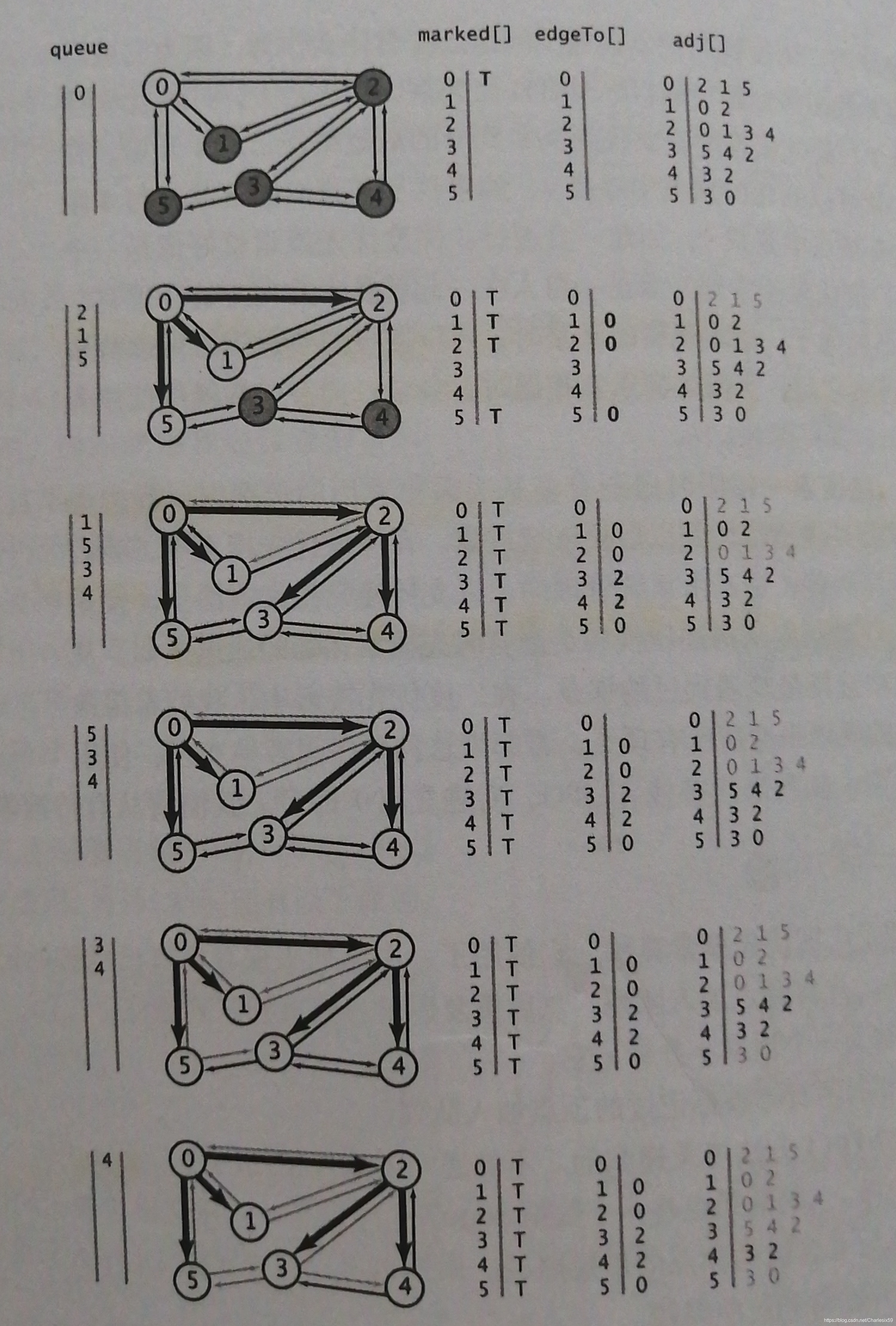
既然上一期说了DFS，这一期当然要来说BFS了。广度优先搜索和DFS还是很相似的，只不过我们会先找出和起点相邻的顶点，然后再依次进入这些顶点，并找到所有与其相邻的顶点，重复上述步骤直到该连通分支的所有节点都被标记。
作者很巧妙的利用了queue的FIFO特性来实现广度优先搜索。(我用STL不是因为懒哈)

路径：

in head.h

class BFS
{
private:
	bool *marked;	//标记数组
	std::vector<std::string> path;	//标记路径的数组
	void bfs(graph g, int v);	//广度优先搜索核心
	bool mark(int v);	//返回顶点是否被标记
public:
	BFS(graph g, int s);	//构造函数，第一个参数是图形类，第二个参数起点
	std::string path_to(int v);		//返回路径的字符串
};

in head.cpp

/*广度优先搜索*/
BFS::BFS(graph g, int s)
{
	marked = new bool[g.numv()];
	std::fill(marked, marked + g.numv(), 0);
	path.resize(g.numv());
	path[s] += std::to_string(s);
	bfs(g, s);		//进入函数
}
bool BFS::mark(int v)
{
	return marked[v];
}
void BFS::bfs(graph g, int v)
{
	marked[v] = true;
	std::queue<int> q;	//用了queue STL，需要引入<queue>
	q.push(v);	
	while (!q.empty())
	{
		int w = q.back();
		q.pop();
		std::vector<int> gv = g.iterator(w);
		for (auto i : gv)
		{
			//printf("%d %d\n", w,marked[w]);
			if (!mark(i))
			{
				path[i] = path[w] + " " + std::to_string(w);	
				marked[w] = true;
				q.push(i);	//q用来储存与当前顶点有连接的顶点
			}
		}
	}
	
}
std::string BFS::path_to(int v)
{
	return path[v];
}

运行结果：

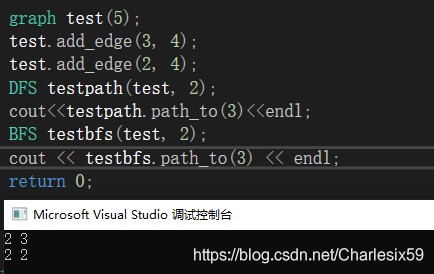
*BFS与DFS产生的路径并不一定相同，相同只是因为碰巧
如果你看过上一期的深度优先搜索，你会发现只有bfs方法与上期略有差别