1.数据结构概述
数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成
存储结构
顺序存储结构
顺序存储结构:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的。数组就是顺序存储结构的典型代表。

链式存储结构
链式存储结构:是把数据元素存放在内存中的任意存储单元里,也就是可以把数据存放在内存的各个位置。这些数据在内存中的地址可以是连续的,也可以是不连续的。

逻辑结构
集合结构
集合结构中的数据元素同属于一个集合,他们之间是并列的关系,除此之外没有其他关系。

线性结构
线性结构中的元素存在一对一的相互关系。

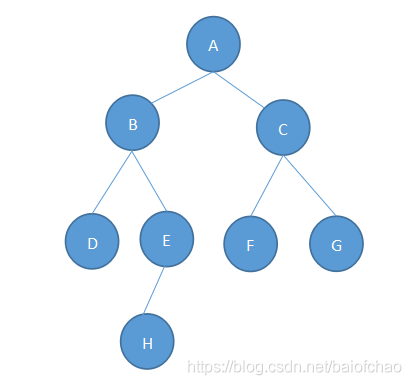
树形结构
树形结构中的元素存在一对多的相互关系。
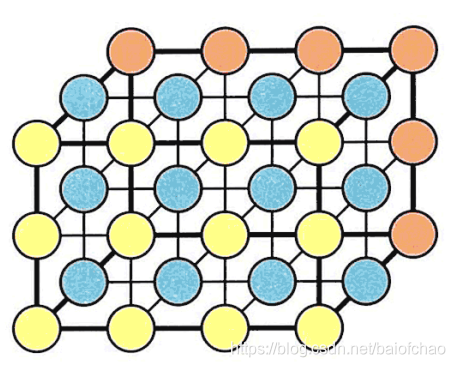
图形结构
图形结构中的元素存在多对多的相互关系。
2.线性结构
数组

数组扩容
import java.util.Arrays;
public class TestOpArray {
public static void main(String[] args) {
//解决数组的长度不可变的问题
int[] arr = new int[] {9,8,7};
//快速查看数组中的元素
System.out.println(Arrays.toString(arr));
//要加入数组的目标元素
int dst=6;
//创建一个新的数组,长度是原数组长度+1
int[] newArr = new int[arr.length+1];
//把原数组中的数据全部复制到新数组中
for(int i=0;i<arr.length;i++) {
newArr[i]=arr[i];
}
//把目标元素放入新数组的最后
newArr[arr.length]=dst;
//新数组替换原数组
arr=newArr;
System.out.println(Arrays.toString(arr));
}
}
数组删除
import java.util.Arrays;
public class TestOpArray2 {
//如何删除数组中的元素
public static void main(String[] args) {
//目标数组
int[] arr = new int[] {9,8,7,6,5,4};
//要删除的元素的下标
int dst = 3;
System.out.println(Arrays.toString(arr));
//创建一个新的数组,长度是原数组的长度-1
int[] newArr = new int[arr.length-1];
//复制原数组中除了要删除的那个元素以外其它的元素
for(int i=0;i<newArr.length;i++) {
//要删除的元素之前的元素
if(i<dst) {
newArr[i]=arr[i];
//要删除的元素之后的元素
}else {
newArr[i]=arr[i+1];
}
}
//新数组替换旧数组
arr=newArr;
System.out.println(Arrays.toString(arr));
}
}
面向对象的数组
查找算法-线性查找
从头到尾一个一个找即可
public class TestSearch {
public static void main(String[] args) {
//目标数组
int[] arr = new int[] {2,3,5,6,8,4,9,0};
//目标元素
int target = 10;
//目标元素所在的下标
int index = -1;
//遍历数组
for(int i=0;i<arr.length;i++) {
if(arr[i]==target) {
index=i;
break;
}
}
//打印目标元素的下标
System.out.println("index:"+index);
}
}
查找算法-二分法查找
针对于有序数组,分半进行查找
public class TestBinarySearch {
public static void main(String[] args) {
//目标数组
int[] arr = new int[]{1,2,3,4,5,6,7,8,9};
//目标元素
int target = 3;
//记录开始位置
int begin = 0;
//记录结束位置
int end = arr.length-1;
//记录中间的位置
int mid = (begin+end)/2;
//记录目标位置
int index=-1;
//循环查找
while(true) {
//判断中间的这个元素是不是要查找的元素
if(arr[mid]==target) {
index=mid;
break;
//中间这个元素不是要查的元素
}else {
//判断中间这个元素是不是比目标元素大
if(arr[mid]>target) {
//把结束位置调整到中间位置前一个位置
end=mid-1;
//中间这个元素比目标元素小
}else {
//把开始位置调整到中间位置的后一个位置
begin = mid+1;
}
//取出新的中间位置
mid=(begin+end)/2;
}
}
System.out.println("index:"+index);
}
}
栈
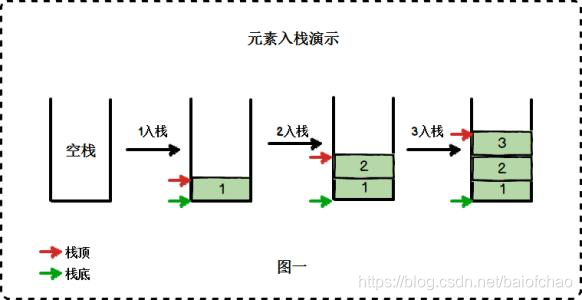
栈实现方式-数组
public class MyStack {
//栈的底层我们使用数组来存储数据
int[] elements;
public MyStack() {
elements = new int[0];
}
//压入元素
public void push(int element) {
// 创建一个新的数组
int[] newArr = new int[elements.length + 1];
// 把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
// 把添加的元素放入新数组中
newArr[elements.length] = element;
// 使用新数组替换旧数组
elements = newArr;
}
//取出栈顶元素
public int pop() {
//栈中没有元素
if(elements.length==0) {
throw new RuntimeException("stack is empty");
}
//取出数组的最后一个元素
int element = elements[elements.length-1];
//创建一个新的数组
int[] newArr = new int[elements.length-1];
//原数组中除了最后一个元素的其它元素都放入新的数组中
for(int i=0;i<elements.length-1;i++) {
newArr[i]=elements[i];
}
//替换数组
elements=newArr;
//返回栈顶元素
return element;
}
//查看栈顶元素
public int peek() {
//栈中没有元素
if(elements.length==0) {
throw new RuntimeException("stack is empty");
}
return elements[elements.length-1];
}
//判断栈是否为空
public boolean isEmpty() {
return elements.length==0;
}
队列


队列实现方式-数组
import javax.swing.text.DefaultStyledDocument.ElementSpec;
public class MyQueue {
int[] elements;
public MyQueue() {
elements=new int[0];
}
//入队
public void add(int element) {
// 创建一个新的数组
int[] newArr = new int[elements.length + 1];
// 把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
// 把添加的元素放入新数组中
newArr[elements.length] = element;
// 使用新数组替换旧数组
elements = newArr;
}
//出队
public int poll() {
//把数组中的第0个元素取出来
int element = elements[0];
//创建一个新的数组
int[] newArr = new int[elements.length-1];
//复制原数组中的元素到新数组中
for(int i=0;i<newArr.length;i++) {
newArr[i]=elements[i+1];
}
//替换数组
elements=newArr;
return element;
}
//判断队列是否为空
public boolean isEmpty() {
return elements.length==0;
}
}
单链表

单链表-构建
//一个节点
public class Node {
//节点内容
int data;
//下一个节点
Node next;
public Node(int data) {
this.data=data;
}
//为节点追回节点
public Node append(Node node) {
//当前节点
Node currentNode = this;
//循环向后找
while(true) {
//取出下一个节点
Node nextNode = currentNode.next;
//如果下一个节点为null,当前节点已经是最后一个节点
if(nextNode==null) {
break;
}
//赋给当前节点
currentNode = nextNode;
}
//把需要追回的节点追加为找到的当前节点的下一个节点
currentNode.next=node;
return this;
}
//插入一个节点做为当前节点的下一个节点
public void after(Node node) {
//取出下一个节点,作为下下一个节点
Node nextNext = next;
//把新节点作为当前节点的下一个节点
this.next=node;
//把下下一个节点设置为新节点的下一个节点
node.next=nextNext;
}
//显示所有节点信息
public void show() {
Node currentNode = this;
while(true) {
System.out.print(currentNode.data+" ");
//取出下一个节点
currentNode=currentNode.next;
//如果是最后一个节点
if(currentNode==null) {
break;
}
}
System.out.println();
}
//删除下一个节点
public void removeNext() {
//取出下下一个节点
Node newNext = next.next;
//把下下一个节点设置为当前节点的下一个节点。
this.next=newNext;
}
//获取下一个节点
public Node next() {
return this.next;
}
//获取节点中的数据
public int getData() {
return this.data;
}
//当前节点是否是最后一个节点
public boolean isLast() {
return next==null;
}
}
测试
public class TestNode {
public static void main(String[] args) {
//创建节点
Node n1 = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
//追加节点
n1.append(n2).append(n3).append(new Node(4));
//取出下一个节点的数据
// System.out.println(n1.next().next().next().getData());
//判断节点是否为最后一个节点
// System.out.println(n1.isLast());
// System.out.println(n1.next().next().next().isLast());
//显示所有节点内容
n1.show();
//删除一个节点
// n1.next().removeNext();
//显示所有节点内容
// n1.show();
//插入一个新节点
Node node = new Node(5);
n1.next().after(node);
n1.show();
}
}
单链表-删除节点
//删除下一个节点
public void removeNext() {
//取出下下一个节点
Node newNext = next.next;
//把下下一个节点设置为当前节点的下一个节点。
this.next=newNext;
}
单链表-插入节点
//插入一个节点做为当前节点的下一个节点
public void after(Node node) {
//取出下一个节点,作为下下一个节点
Node nextNext = next;
//把新节点作为当前节点的下一个节点
this.next=node;
//把下下一个节点设置为新节点的下一个节点
node.next=nextNext;
}
循环链表

循环链表-构建
//一个节点
public class LoopNode {
//节点内容
int data;
//下一个节点
LoopNode next=this;//与单链表的不同点
public LoopNode(int data) {
this.data=data;
}
//插入一个节点做为当前节点的下一个节点
public void after(LoopNode node) {
//取出下一个节点,作为下下一个节点
LoopNode nextNext = next;
//把新节点作为当前节点的下一个节点
this.next=node;
//把下下一个节点设置为新节点的下一个节点
node.next=nextNext;
}
//删除下一个节点
public void removeNext() {
//取出下下一个节点
LoopNode newNext = next.next;
//把下下一个节点设置为当前节点的下一个节点。
this.next=newNext;
}
//获取下一个节点
public LoopNode next() {
return this.next;
}
//获取节点中的数据
public int getData() {
return this.data;
}
}
双向链表
两种如图:空的双向循环链表,非空的双向循环链表
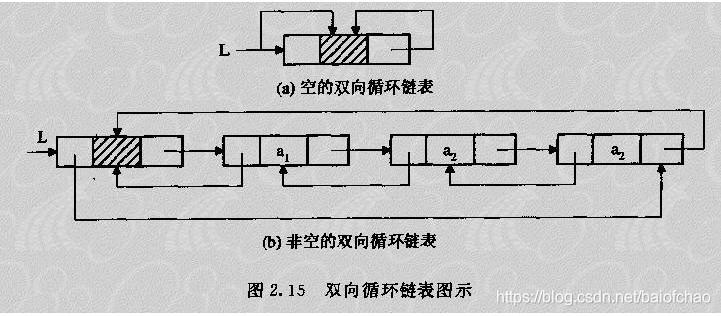
循环双向链表-代码实现
public class DoubleNode {
//上一个节点
DoubleNode pre=this;
//下一个节点
DoubleNode next=this;
//节点数据
int data;
public DoubleNode(int data) {
this.data=data;
}
//增节点
public void after(DoubleNode node) {
//原来的下一个节点
DoubleNode nextNext = next;
//把新节点做为当前节点的下一个节点
this.next=node;
//把当前节点做新节点的前一个节点
node.pre=this;
//让原来的下一个节点作新节点的下一个节点
node.next=nextNext;
//让原来的下一个节点的上一个节点为新节点
nextNext.pre=node;
}
//下一个节点
public DoubleNode next() {
return this.next;
}
//上一个节点
public DoubleNode pre() {
return this.pre;
}
//获取数据
public int getData() {
return this.data;
}
}
递归
递归:在一个方法(函数)的内部调用该方法(函数)本身的编程方式
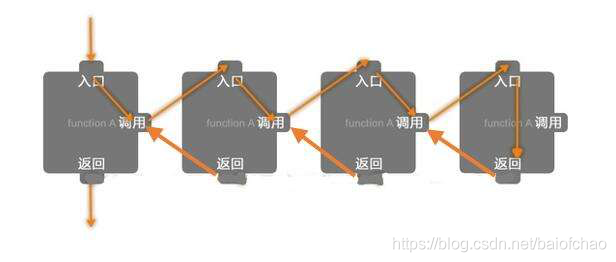
应用一: 斐波那契
public class TestFebonacci {
public static void main(String[] args) {
//斐波那契数列:1 1 2 3 5 8 13
int i = febonacci(7);
System.out.println(i);
}
//打印第n项斐波那契数列
public static int febonacci(int i) {
if(i==1 || i==2) {
return 1;
}else {
return febonacci(i-1)+febonacci(i-2);
}
}
}
应用二 :汉诺塔问题

public class TestHanoi {
public static void main(String[] args) {
hanoi(5,'A','B','C');
}
/**
* @param n 共有N个盘子
* @param from 开始的柱子
* @param in 中间的柱子
* @param to 目标柱子
* 无论有多少个盘子,都认为只有两个。上面的所有盘子和最下面一个盘子。
*/
public static void hanoi(int n,char from,char in,char to) {
//只有一个盘子。
if(n==1) {
System.out.println("第1个盘子从"+from+"移到"+to);
//无论有多少个盘子,都认为只有两个。上面的所有盘子和最下面一个盘子。
}else {
//移动上面所有的盘子到中间位置
hanoi(n-1,from,to,in);
//移动下面的盘子
System.out.println("第"+n+"个盘子从"+from+"移到"+to);
//把上面的所有盘子从中间位置移到目标位置
hanoi(n-1,in,from,to);
}
}
}
3. 排序算法
时间复杂度,空间复杂度
时间复杂度
概念
一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示。
若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
T(n)不同,但时间复杂度可能相同。如:T(n)=n2+5n+6与T(n)=3n2+3n+2它们的T(n)不同,但时间复杂度相同,都为O(n^2)。
常见的时间复杂度
常数阶O(1)
对数阶O(log2n)
线性阶O(n)
线性对数阶O(nlog2n)
平方阶O(n2)
立方阶O(n3)
k次方阶O(nk)
指数阶O(2n)
随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
计算时间复杂度方法
用常数1代替运行时间中的所有加法常树
修改后的运行次数函数中,只保留最高阶项1
去除最高阶项的系数
平均时间复杂度和最坏时间复杂度
平均时间复杂度:是指所有可能的输入实例均以等概率出现的情况下,该算法的运行时间。
最坏情况下的时间复杂度称最坏时间复杂度:一般讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限这就保证了算法的运行时间不会比最坏情况更长。
空间复杂度
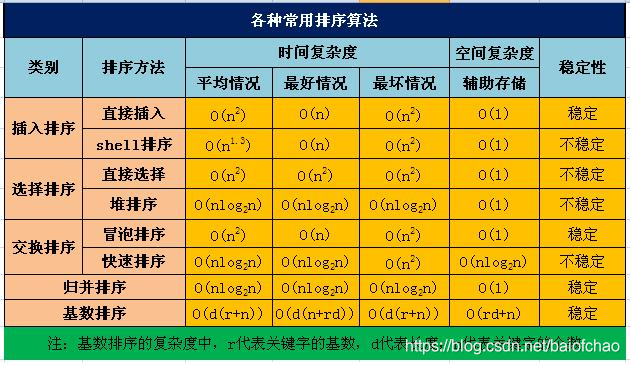
排序算法
 ### 不同算法之间比较
### 不同算法之间比较
冒泡排序
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] arr=new int[] {5,7,2,9,4,1,0,5,7};
System.out.println(Arrays.toString(arr));
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
//冒泡排序
/**
* 5,7,2,9,4,1,0,5,7 共需要比较length-1轮
* 5,7,2,9,4,1,0,5,7
* 5,2,7,9,4,1,0,5,7
* 5,2,7,4,1,0,5,7,9
* 2,5
*/
public static void bubbleSort(int[] arr) {
//控制共比较多少轮
for(int i=0;i<arr.length-1;i++) {
//控制比较的次数
for(int j=0;j<arr.length-1-i;j++) {
if(arr[j]>arr[j+1]) {
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
}
快速排序
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] arr = new int[] {3,4,6,7,2,7,2,8,0,9,1};
quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr,int start,int end) {
if(start<end) {
//把数组中的第0个数字做为标准数
int stard=arr[start];
//记录需要排序的下标
int low=start;
int high=end;
//循环找比标准数大的数和比标准数小的数
while(low<high) {
//右边的数字比标准数大
while(low<high&&stard<=arr[high]) {
high--;
}
//使用右边的数字替换左边的数
arr[low]=arr[high];
//如果左边的数字比标准数小
while(low<high&&arr[low]<=stard) {
low++;
}
arr[high]=arr[low];
}
//把标准数赋给低所在的位置的元素
arr[low]=stard;
//处理所有的小的数字
quickSort(arr, start, low);
//处理所有的大的数字
quickSort(arr, low+1, end);
}
}
}
插入排序
import java.util.Arrays;
public class InsertSort {
public static void main(String[] args) {
int[] arr = new int[] {5,3,2,8,5,9,1,0};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
//插入排序
public static void insertSort(int[] arr) {
//遍历所有的数字
for(int i=1;i<arr.length;i++) {
//如果当前数字比前一个数字小
if(arr[i]<arr[i-1]) {
//把当前遍历数字存起来
int temp=arr[i];
int j;
//遍历当前数字前面所有的数字
for(j=i-1;j>=0&&temp<arr[j];j--) {
//把前一个数字赋给后一个数字
arr[j+1]=arr[j];
}
//把临时变量(外层for循环的当前元素)赋给不满足条件的后一个元素
arr[j+1]=temp;
}
}
}
}
希尔排序
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] arr = new int[] { 3, 5, 2, 7, 8, 1, 2, 0, 4, 7, 4, 3, 8 };
System.out.println(Arrays.toString(arr));
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
int k = 1;
// 遍历所有的步长
for (int d = arr.length / 2; d > 0; d /= 2) {
// 遍历所有有元素
for (int i = d; i < arr.length; i++) {
// 遍历本组中所有的元素
for (int j = i - d; j >= 0; j -= d) {
// 如果当前元素大于加上步长后的那个元素
if (arr[j] > arr[j + d]) {
int temp = arr[j];
arr[j] = arr[j + d];
arr[j + d] = temp;
}
}
}
System.out.println("第" + k + "次排序结果:" + Arrays.toString(arr));
k++;
}
}
}
选择排序-简单选择排序
import java.util.Arrays;
public class SelectSort {
public static void main(String[] args) {
int[] arr = new int[] {3,4,5,7,1,2,0,3,6,8};
selectSort(arr);
System.out.println(Arrays.toString(arr));
}
//选择排序
public static void selectSort(int[] arr) {
//遍历所有的数
for(int i=0;i<arr.length;i++) {
int minIndex=i;
//把当前遍历的数和后面所有的数依次进行比较,并记录下最小的数的下标
for(int j=i+1;j<arr.length;j++) {
//如果后面比较的数比记录的最小的数小。
if(arr[minIndex]>arr[j]) {
//记录下最小的那个数的下标
minIndex=j;
}
}
//如果最小的数和当前遍历数的下标不一致,说明下标为minIndex的数比当前遍历的数更小。
if(i!=minIndex) {
int temp=arr[i];
arr[i]=arr[minIndex];
arr[minIndex]=temp;
}
}
}
}
归并排序
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] arr = new int[] {1,3,5,2,4,6,8,10};
System.out.println(Arrays.toString(arr));
mergeSort(arr, 0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
//归并排序
public static void mergeSort(int[] arr,int low,int high) {
int middle=(high+low)/2;
if(low<high) {
//处理左边
mergeSort(arr, low, middle);
//处理右边
mergeSort(arr, middle+1, high);
//归并
merge(arr,low,middle,high);
}
}
public static void merge(int[] arr,int low,int middle, int high) {
//用于存储归并后的临时数组
int[] temp = new int[high-low+1];
//记录第一个数组中需要遍历的下标
int i=low;
//记录第二个数组中需要遍历的下标
int j=middle+1;
//用于记录在临时数组中存放的下标
int index=0;
//遍历两个数组取出小的数字,放入临时数组中
while(i<=middle&&j<=high) {
//第一个数组的数据更小
if(arr[i]<=arr[j]) {
//把小的数据放入临时数组中
temp[index]=arr[i];
//让下标向后移一位;
i++;
}else {
temp[index]=arr[j];
j++;
}
index++;
}
//处理多余的数据
while(j<=high) {
temp[index]=arr[j];
j++;
index++;
}
while(i<=middle) {
temp[index]=arr[i];
i++;
index++;
}
//把临时数组中的数据重新存入原数组
for(int k=0;k<temp.length;k++) {
arr[k+low]=temp[k];
}
}
}
基数排序
适用于大小数都有的场景
基数排序-数组方式
原理
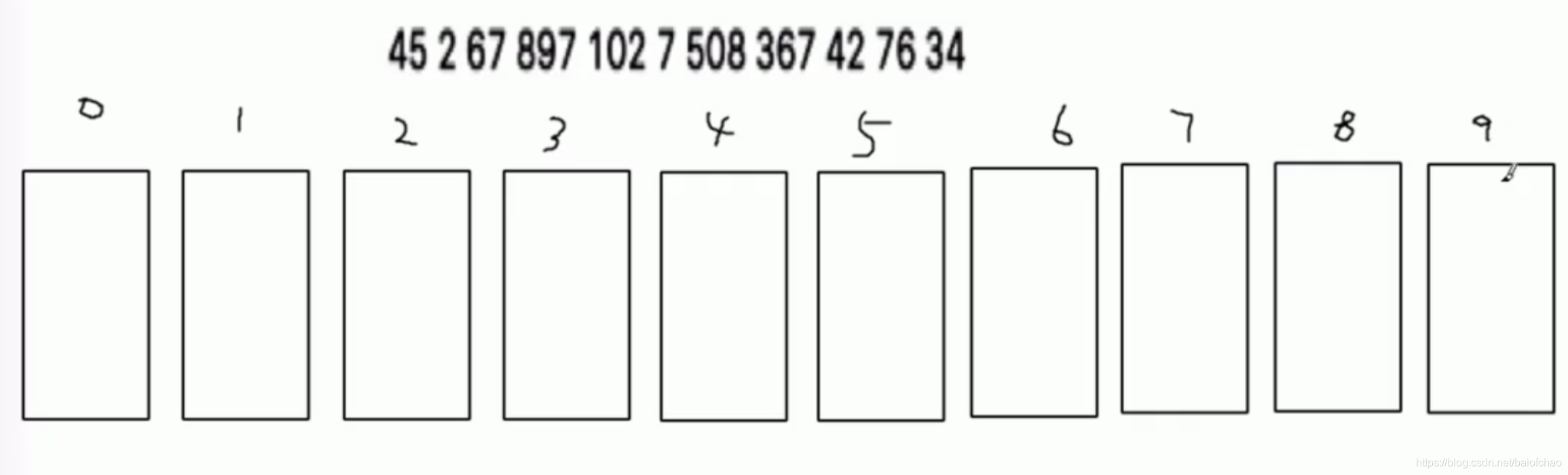
 从0->9依次取出数据
从0->9依次取出数据

 从0-9依次取出数据
从0-9依次取出数据
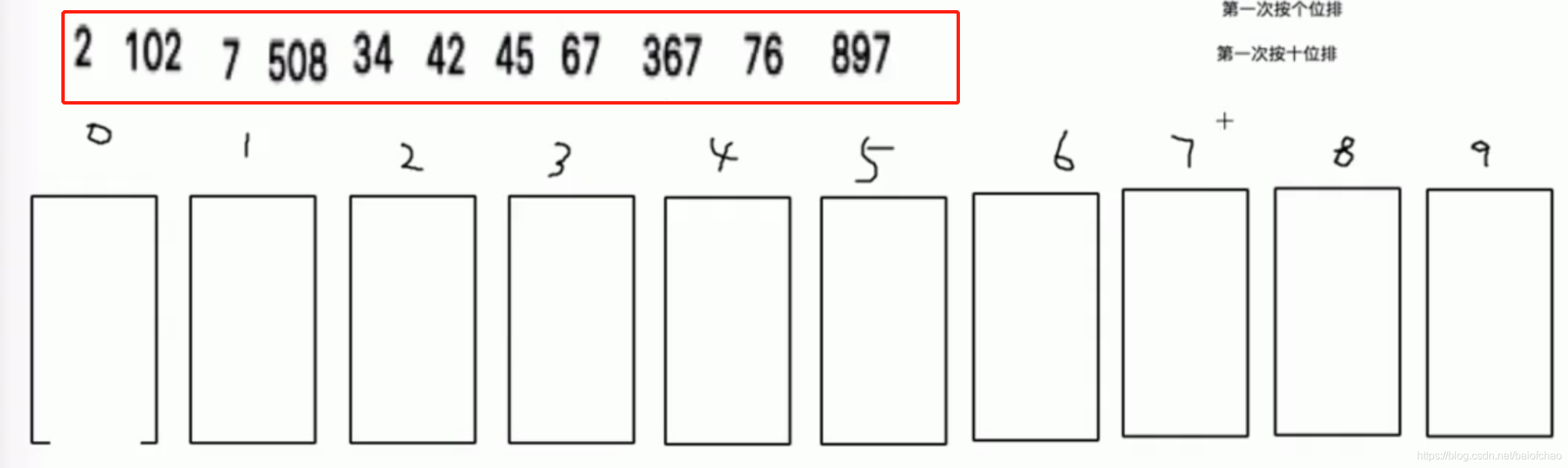
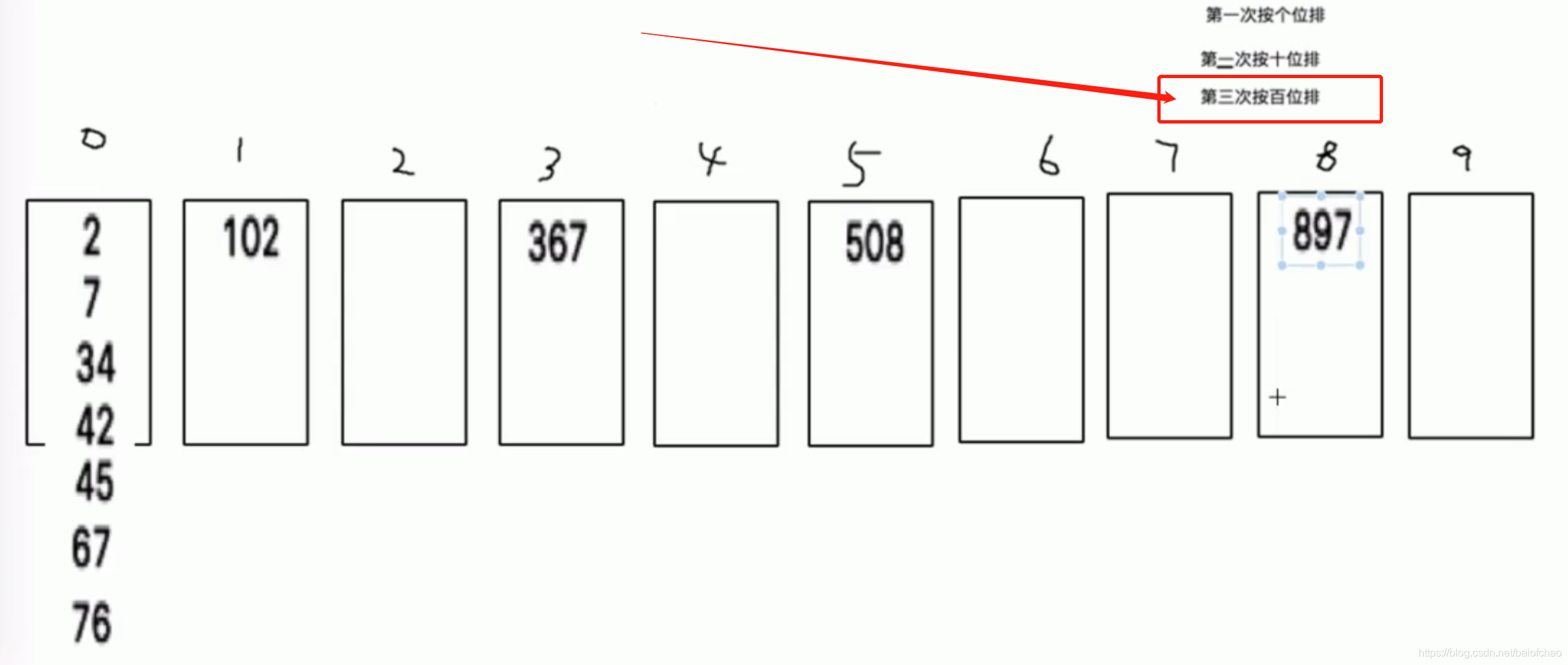
依然从0->9依次取出
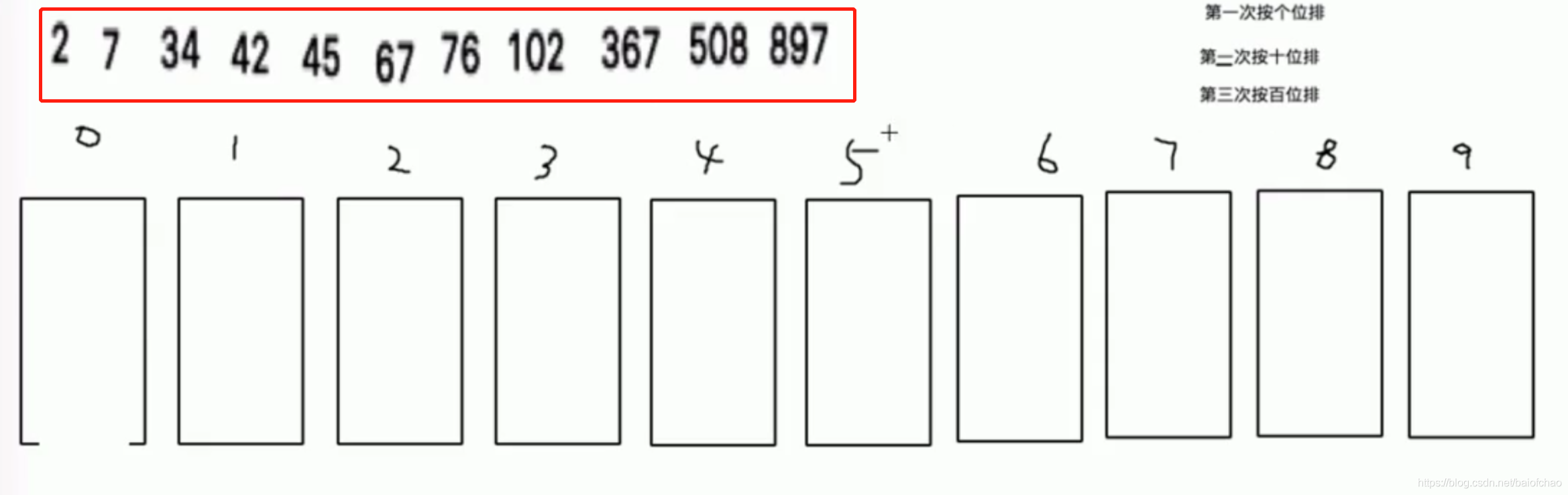
至此顺序已经OK
排序次数取决于数字的最大位数
实现
import java.util.Arrays;
public class RadixSort {
public static void main(String[] args) {
int[] arr = new int[] {23,6,189,45,9,287,56,1,798,34,65,652,5};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//存最数组中最大的数字
int max=Integer.MIN_VALUE;
for(int i=0;i<arr.length;i++) {
if(arr[i]>max) {
max=arr[i];
}
}
//计算最大数字是几位数
int maxLength = (max+"").length();
//用于临时存储数据的数组
int[][] temp = new int[10][arr.length];
//用于记录在temp中相应的数组中存放的数字的数量
int[] counts = new int[10];
//根据最大长度的数决定比较的次数
for(int i=0,n=1;i<maxLength;i++,n*=10) {
//把每一个数字分别计算余数
for(int j=0;j<arr.length;j++) {
//计算余数
int ys = arr[j]/n%10;
//把当前遍历的数据放入指定的数组中
temp[ys][counts[ys]] = arr[j];
//记录数量
counts[ys]++;
}
//记录取的元素需要放的位置
int index=0;
//把数字取出来
for(int k=0;k<counts.length;k++) {
//记录数量的数组中当前余数记录的数量不为0
if(counts[k]!=0) {
//循环取出元素
for(int l=0;l<counts[k];l++) {
//取出元素
arr[index] = temp[k][l];
//记录下一个位置
index++;
}
//把数量置为0
counts[k]=0;
}
}
}
}
}
基础排序-队列实现
import java.util.Arrays;
import demo2.MyQueue;
public class RadixQueueSort {
public static void main(String[] args) {
int[] arr = new int[] {23,6,189,45,9,287,56,1,798,34,65,652,5};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//存最数组中最大的数字
int max=Integer.MIN_VALUE;
for(int i=0;i<arr.length;i++) {
if(arr[i]>max) {
max=arr[i];
}
}
//计算最大数字是几位数
int maxLength = (max+"").length();
//用于临时存储数据的队列的数组
MyQueue[] temp = new MyQueue[10];
//为队列数组赋值
for(int i=0;i<temp.length;i++) {
temp[i]=new MyQueue();
}
//根据最大长度的数决定比较的次数
for(int i=0,n=1;i<maxLength;i++,n*=10) {
//把每一个数字分别计算余数
for(int j=0;j<arr.length;j++) {
//计算余数
int ys = arr[j]/n%10;
//把当前遍历的数据放入指定的队列中
temp[ys].add(arr[j]);
}
//记录取的元素需要放的位置
int index=0;
//把所有队列中的数字取出来
for(int k=0;k<temp.length;k++) {
//循环取出元素
while(!temp[k].isEmpty()) {
//取出元素
arr[index] = temp[k].poll();
//记录下一个位置
index++;
}
}
}
}
}
public class MyQueue {
int[] elements;
public MyQueue() {
elements=new int[0];
}
//入队
public void add(int element) {
// 创建一个新的数组
int[] newArr = new int[elements.length + 1];
// 把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
// 把添加的元素放入新数组中
newArr[elements.length] = element;
// 使用新数组替换旧数组
elements = newArr;
}
//出队
public int poll() {
//把数组中的第0个元素取出来
int element = elements[0];
//创建一个新的数组
int[] newArr = new int[elements.length-1];
//复制原数组中的元素到新数组中
for(int i=0;i<newArr.length;i++) {
newArr[i]=elements[i+1];
}
//替换数组
elements=newArr;
return element;
}
//判断队列是否为空
public boolean isEmpty() {
return elements.length==0;
}
}
4. 树
树概念
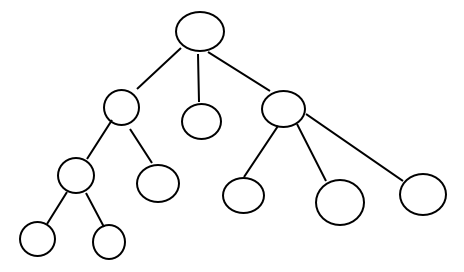
- 根节点
- 双亲节点
- 子节点
- 路径
- 节点的度
- 节点的权
- 叶子节点
- 子树
- 层
- 树的高度
- 森林
二叉树
概念
二叉树:任何一个节点的子节点数量不超2
二叉树的子节点分左节点和右节点
分类
满二叉树
完全二叉树

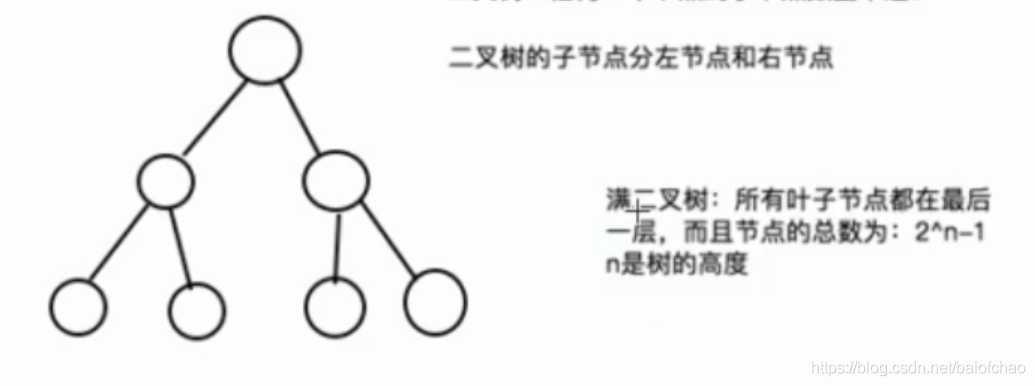
链式存储的二叉树
创建
public class Node {
//节点的权
int value;
//左儿子
Node leftNode;
//右儿子
Node rightNode;
public Node(int value) {
this.value=value;
}
//设置左儿子
public void setLeftNode(Node leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(Node rightNode) {
this.rightNode = rightNode;
}
//前序遍历
public void frontShow() {
//先遍历当前节点的内容
System.out.println(value);
//左节点
if(leftNode!=null) {
leftNode.frontShow();
}
//右节点
if(rightNode!=null) {
rightNode.frontShow();
}
}
//中序遍历
public void midShow() {
//左子节点
if(leftNode!=null) {
leftNode.midShow();
}
//当前节点
System.out.println(value);
//右子节点
if(rightNode!=null) {
rightNode.midShow();
}
}
//后序遍历
public void afterShow() {
//左子节点
if(leftNode!=null) {
leftNode.afterShow();
}
//右子节点
if(rightNode!=null) {
rightNode.afterShow();
}
//当前节点
System.out.println(value);
}
//前序查找
public Node frontSearch(int i) {
Node target=null;
//对比当前节点的值
if(this.value==i) {
return this;
//当前节点的值不是要查找的节点
}else {
//查找左儿子
if(leftNode!=null) {
//有可能可以查到,也可以查不到,查不到的话,target还是一个null
target = leftNode.frontSearch(i);
}
//如果不为空,说明在左儿子中已经找到
if(target!=null) {
return target;
}
//查找右儿子
if(rightNode!=null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
//删除一个子树
public void delete(int i) {
Node parent = this;
//判断左儿子
if(parent.leftNode!=null&&parent.leftNode.value==i) {
parent.leftNode=null;
return;
}
//判断右儿子
if(parent.rightNode!=null&&parent.rightNode.value==i) {
parent.rightNode=null;
return;
}
//递归检查并删除左儿子
parent=leftNode;
if(parent!=null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent=rightNode;
if(parent!=null) {
parent.delete(i);
}
}
}
public class BinaryTree {
Node root;
//设置根节点
public void setRoot(Node root) {
this.root = root;
}
//获取根节点
public Node getRoot() {
return root;
}
public void frontShow() {
if(root!=null) {
root.frontShow();
}
}
public void midShow() {
if(root!=null) {
root.midShow();
}
}
public void afterShow() {
if(root!=null) {
root.afterShow();
}
}
public Node frontSearch(int i) {
return root.frontSearch(i);
}
public void delete(int i) {
if(root.value==i) {
root=null;
}else {
root.delete(i);
}
}
}
测试
public class TestBinaryTree {
public static void main(String[] args) {
//创建一颗树
BinaryTree binTree = new BinaryTree();
//创建一个根节点
Node root = new Node(1);
//把根节点赋给树
binTree.setRoot(root);
//创建一个左节点
Node rootL = new Node(2);
//把新创建的节点设置为根节点的子节点
root.setLeftNode(rootL);
//创建一个右节点
Node rootR = new Node(3);
//把新创建的节点设置为根节点的子节点
root.setRightNode(rootR);
//为第二层的左节点创建两个子节点
rootL.setLeftNode(new Node(4));
rootL.setRightNode(new Node(5));
//为第二层的右节点创建两个子节点
rootR.setLeftNode(new Node(6));
rootR.setRightNode(new Node(7));
//前序遍历树
binTree.frontShow();
System.out.println("===============");
//中序遍历
binTree.midShow();
System.out.println("===============");
//后序遍历
binTree.afterShow();
System.out.println("===============");
//前序查找
Node result = binTree.frontSearch(5);
System.out.println(result);
System.out.println("===============");
//删除一个子树
binTree.delete(4);
binTree.frontShow();
}
}
遍历
- 前序遍历
- 中序遍历
- 后序遍历
前序遍历
见【构建】代码里面
中序遍历
见【构建】代码里面
后序遍历
见【构建】代码里面
查找
查找也有三种方法(前序/中序/后序查找)
示例前序方式
见【构建】代码里面
删除
见【构建】代码里面
顺序存储的二叉树
顺序存储的二叉树通常只考虑完全二叉树
性质
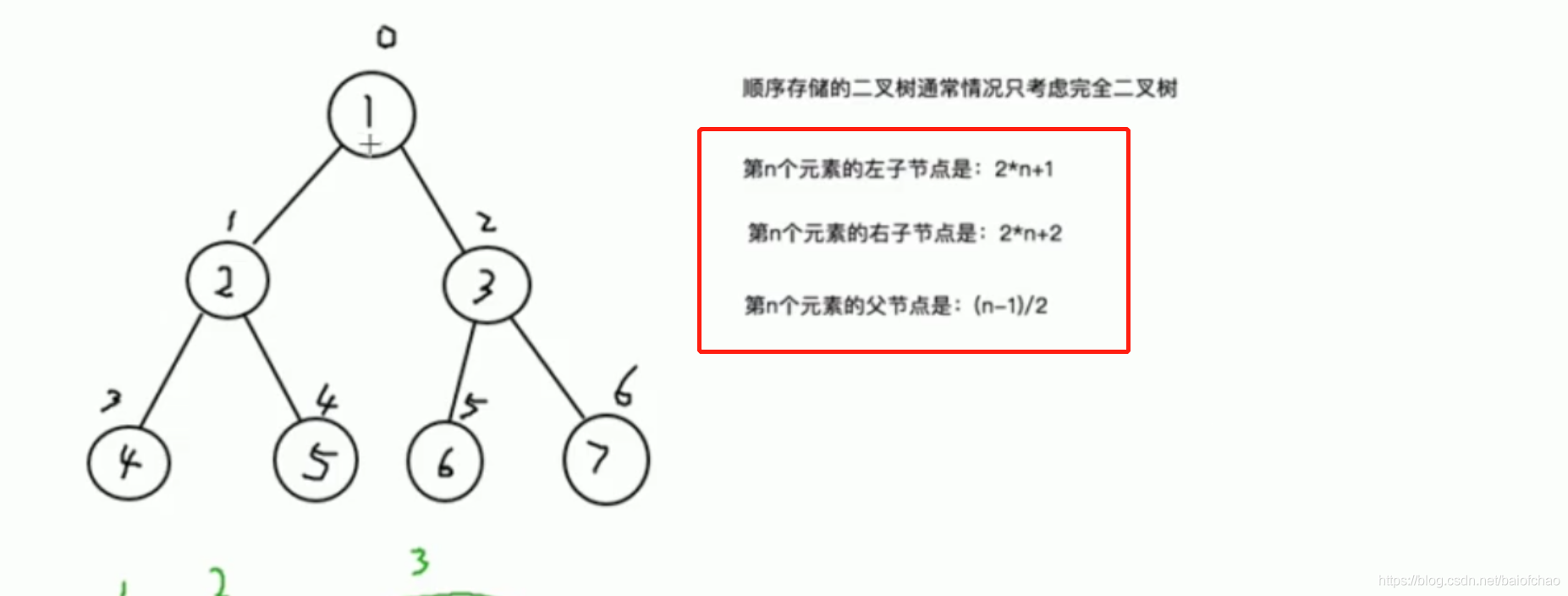
遍历
public class ArrayBinaryTree {
int[] data;
public ArrayBinaryTree(int[] data) {
this.data=data;
}
public void frontShow() {
frontShow(0);
}
//前序遍历
public void frontShow(int index) {
if(data==null||data.length==0) {
return;
}
//先遍历当前节点的内容
System.out.println(data[index]);
//2*index+1:处理左子树
if(2*index+1<data.length) {
frontShow(2*index+1);
}
//2*index+2:处理右子树
if(2*index+2<data.length) {
frontShow(2*index+2);
}
}
}
测试
public class TestArrayBinaryTree {
public static void main(String[] args) {
int[] data = new int[] {1,2,3,4,5,6,7};
ArrayBinaryTree tree = new ArrayBinaryTree(data);
//前序遍历
tree.frontShow();
}
}
堆
概念
大顶堆:所有父节点都大于其子节点
小顶堆:所欲父节点都小于其子节点
升序排序使用大顶堆
降序排序使用小顶堆
大顶堆示例:
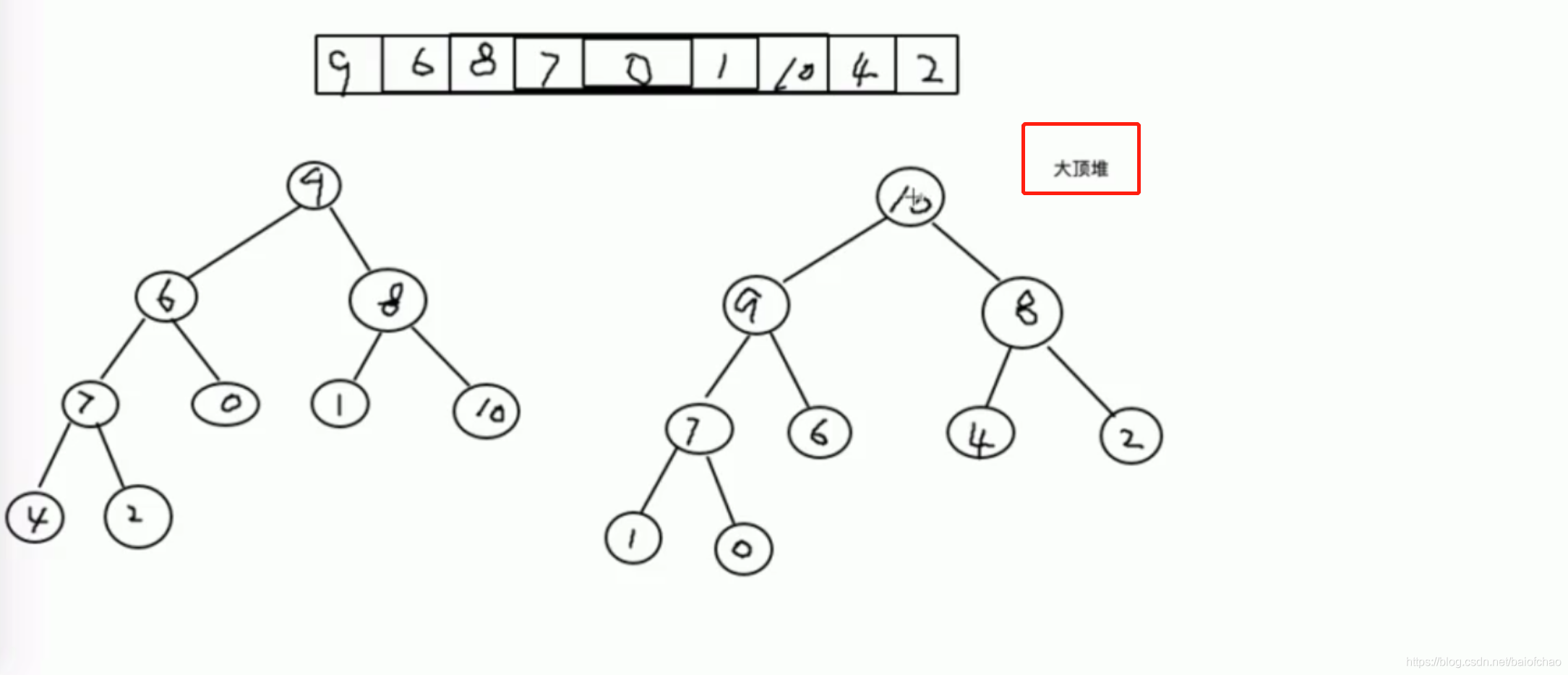
二叉树转为大顶堆
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[] {9,6,8,7,0,1,10,4,2};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
//开始位置是最后一个非叶子节点,即最后一个节点的父节点
int start = (arr.length-1)/2;
//调整为大顶堆
for(int i=start;i>=0;i--) {
maxHeap(arr, arr.length, i);
}
//先把数组中的第0个和堆中的最后一个数交换位置,再把前面的处理为大顶堆
for(int i=arr.length-1;i>0;i--) {
int temp = arr[0];
arr[0]=arr[i];
arr[i]=temp;
maxHeap(arr, i, 0);
}
}
public static void maxHeap(int[] arr,int size,int index) {
//左子节点
int leftNode = 2*index+1;
//右子节点
int rightNode = 2*index+2;
int max = index;
//和两个子节点分别对比,找出最大的节点
if(leftNode<size&&arr[leftNode]>arr[max]) {
max=leftNode;
}
if(rightNode<size&&arr[rightNode]>arr[max]) {
max=rightNode;
}
//交换位置
if(max!=index) {
int temp=arr[index];
arr[index]=arr[max];
arr[max]=temp;
//交换位置以后,可能会破坏之前排好的堆,所以,之前的排好的堆需要重新调整
maxHeap(arr, size, max);
}
}
}
堆排序
通过转成大顶堆,然后用第一位和最后一位交换,交换后的最后一位即是最大值
堆排序
通过转成大顶堆,然后用第一位和最后一位交换,交换后的最后一位即是最大值
public static void heapSort(int[] arr) {
//开始位置是最后一个非叶子节点,即最后一个节点的父节点
int start = (arr.length-1)/2;
//调整为大顶堆
for(int i=start;i>=0;i--) {
maxHeap(arr, arr.length, i);
}
//先把数组中的第0个和堆中的最后一个数交换位置,再把前面的处理为大顶堆
for(int i=arr.length-1;i>0;i--) {
int temp = arr[0];
arr[0]=arr[i];
arr[i]=temp;
maxHeap(arr, i, 0);
}
}
线索二叉树
概念
形成一个双向链表
中序/前序/后序线索化二叉树
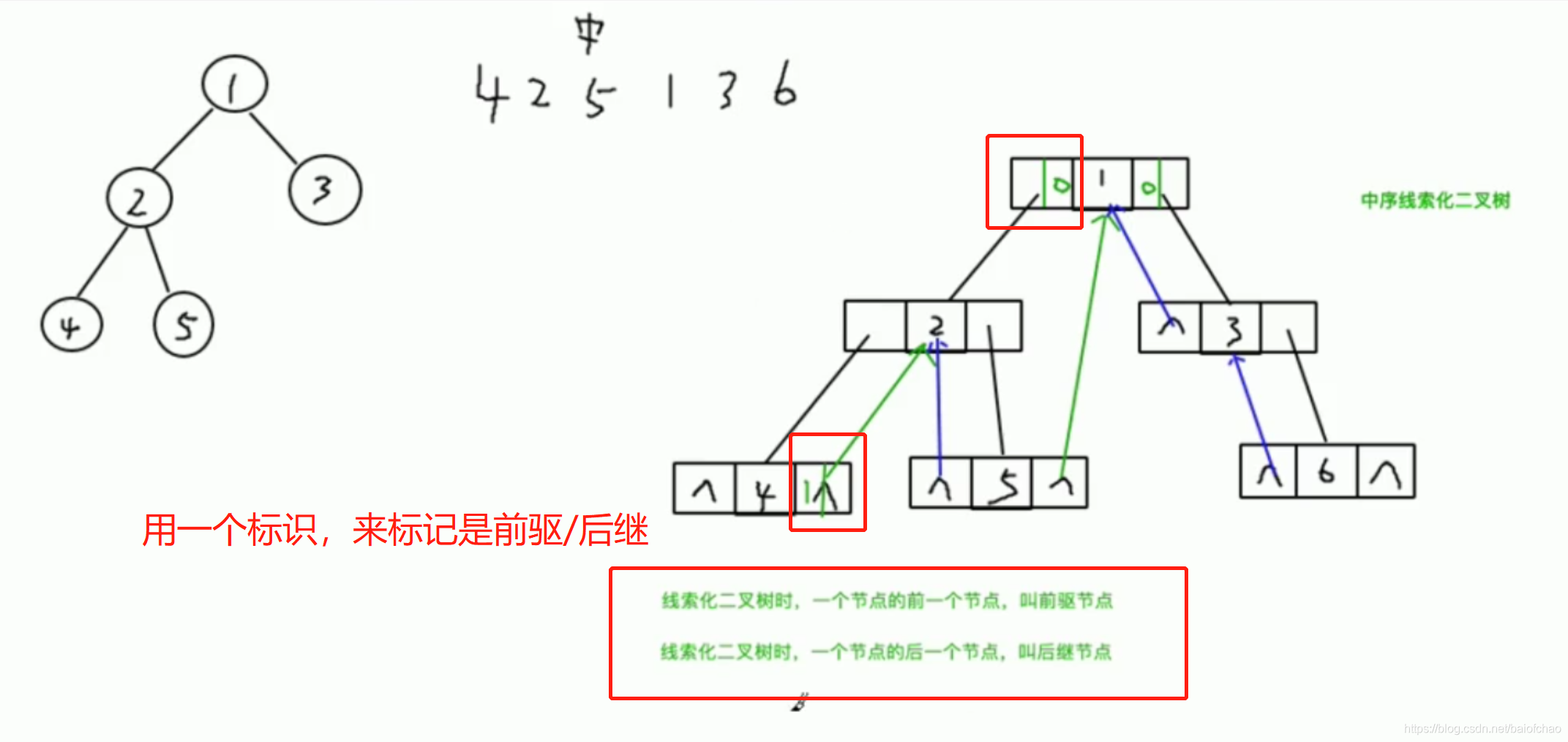
实现
public class ThreadedNode {
//节点的权
int value;
//左儿子
ThreadedNode leftNode;
//右儿子
ThreadedNode rightNode;
//标识指针类型
int leftType;
int rightType;
public ThreadedNode(int value) {
this.value=value;
}
//设置左儿子
public void setLeftNode(ThreadedNode leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(ThreadedNode rightNode) {
this.rightNode = rightNode;
}
//前序遍历
public void frontShow() {
//先遍历当前节点的内容
System.out.println(value);
//左节点
if(leftNode!=null) {
leftNode.frontShow();
}
//右节点
if(rightNode!=null) {
rightNode.frontShow();
}
}
//中序遍历
public void midShow() {
//左子节点
if(leftNode!=null) {
leftNode.midShow();
}
//当前节点
System.out.println(value);
//右子节点
if(rightNode!=null) {
rightNode.midShow();
}
}
//后序遍历
public void afterShow() {
//左子节点
if(leftNode!=null) {
leftNode.afterShow();
}
//右子节点
if(rightNode!=null) {
rightNode.afterShow();
}
//当前节点
System.out.println(value);
}
//前序查找
public ThreadedNode frontSearch(int i) {
ThreadedNode target=null;
//对比当前节点的值
if(this.value==i) {
return this;
//当前节点的值不是要查找的节点
}else {
//查找左儿子
if(leftNode!=null) {
//有可能可以查到,也可以查不到,查不到的话,target还是一个null
target = leftNode.frontSearch(i);
}
//如果不为空,说明在左儿子中已经找到
if(target!=null) {
return target;
}
//查找右儿子
if(rightNode!=null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
//删除一个子树
public void delete(int i) {
ThreadedNode parent = this;
//判断左儿子
if(parent.leftNode!=null&&parent.leftNode.value==i) {
parent.leftNode=null;
return;
}
//判断右儿子
if(parent.rightNode!=null&&parent.rightNode.value==i) {
parent.rightNode=null;
return;
}
//递归检查并删除左儿子
parent=leftNode;
if(parent!=null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent=rightNode;
if(parent!=null) {
parent.delete(i);
}
}
}
public class ThreadedBinaryTree {
ThreadedNode root;
//用于临时存储前驱节点
ThreadedNode pre=null;
//遍历线索二叉树
public void threadIterate() {
//用于临时存储当前遍历节点
ThreadedNode node = root;
while(node!=null) {
//循环找到最开始的节点
while(node.leftType==0) {
node=node.leftNode;
}
//打印当前节点的值
System.out.println(node.value);
//如果当前节点的右指针指向的是后继节点,可能后继节点还有后继节点、
while(node.rightType==1) {
node=node.rightNode;
System.out.println(node.value);
}
//替换遍历的节点
node=node.rightNode;
}
}
//设置根节点
public void setRoot(ThreadedNode root) {
this.root = root;
}
//中序线索化二叉树
public void threadNodes() {
threadNodes(root);
}
public void threadNodes(ThreadedNode node) {
//当前节点如果为null,直接返回
if(node==null) {
return;
}
//处理左子树
threadNodes(node.leftNode);
//处理前驱节点
if(node.leftNode==null){
//让当前节点的左指针指向前驱节点
node.leftNode=pre;
//改变当前节点左指针的类型
node.leftType=1;
}
//处理前驱的右指针,如果前驱节点的右指针是null(没有指下右子树)
if(pre!=null&&pre.rightNode==null) {
//让前驱节点的右指针指向当前节点
pre.rightNode=node;
//改变前驱节点的右指针类型
pre.rightType=1;
}
//每处理一个节点,当前节点是下一个节点的前驱节点
pre=node;
//处理右子树
threadNodes(node.rightNode);
}
//获取根节点
public ThreadedNode getRoot() {
return root;
}
//前序遍历
public void frontShow() {
if(root!=null) {
root.frontShow();
}
}
//中序遍历
public void midShow() {
if(root!=null) {
root.midShow();
}
}
//后序遍历
public void afterShow() {
if(root!=null) {
root.afterShow();
}
}
//前序查找
public ThreadedNode frontSearch(int i) {
return root.frontSearch(i);
}
//删除子树
public void delete(int i) {
if(root.value==i) {
root=null;
}else {
root.delete(i);
}
}
}
public class TestThreadedBinaryTree {
public static void main(String[] args) {
//创建一颗树
ThreadedBinaryTree binTree = new ThreadedBinaryTree();
//创建一个根节点
ThreadedNode root = new ThreadedNode(1);
//把根节点赋给树
binTree.setRoot(root);
//创建一个左节点
ThreadedNode rootL = new ThreadedNode(2);
//把新创建的节点设置为根节点的子节点
root.setLeftNode(rootL);
//创建一个右节点
ThreadedNode rootR = new ThreadedNode(3);
//把新创建的节点设置为根节点的子节点
root.setRightNode(rootR);
//为第二层的左节点创建两个子节点
rootL.setLeftNode(new ThreadedNode(4));
ThreadedNode fiveNode = new ThreadedNode(5);
rootL.setRightNode(fiveNode);
//为第二层的右节点创建两个子节点
rootR.setLeftNode(new ThreadedNode(6));
rootR.setRightNode(new ThreadedNode(7));
//中序遍历树
binTree.midShow();
System.out.println("===============");
//中前线索化二叉树
binTree.threadNodes();
binTree.threadIterate();
}
}
遍历
//遍历线索二叉树
public void threadIterate() {
//用于临时存储当前遍历节点
ThreadedNode node = root;
while(node!=null) {
//循环找到最开始的节点
while(node.leftType==0) {
node=node.leftNode;
}
//打印当前节点的值
System.out.println(node.value);
//如果当前节点的右指针指向的是后继节点,可能后继节点还有后继节点、
while(node.rightType==1) {
node=node.rightNode;
System.out.println(node.value);
}
//替换遍历的节点
node=node.rightNode;
}
}
赫夫曼树
概念
最优二叉树:它是n个带权叶子结点构成的所有二叉树中,带权路径长度最小的二叉树。
叶节点的带权路径
树的带权路径长度WPL:树的带权路径长度WPL(weighted path length):树中所有叶子结点的带权路径长度之和。
 (a)WPL=9x2+4x2+5x2+2x2=18+8+10+4=40
(a)WPL=9x2+4x2+5x2+2x2=18+8+10+4=40
(b)WPL=9x1+5x2+4x3+2x3=9+10+12+6=37
(c)WPL=4x1+2x2+5x3+9x3=4+4+15+27=50
权值越大的结点离根结点越近的二叉树才是最优二叉树。
构建方式
 最终结构即为:赫夫曼树
最终结构即为:赫夫曼树
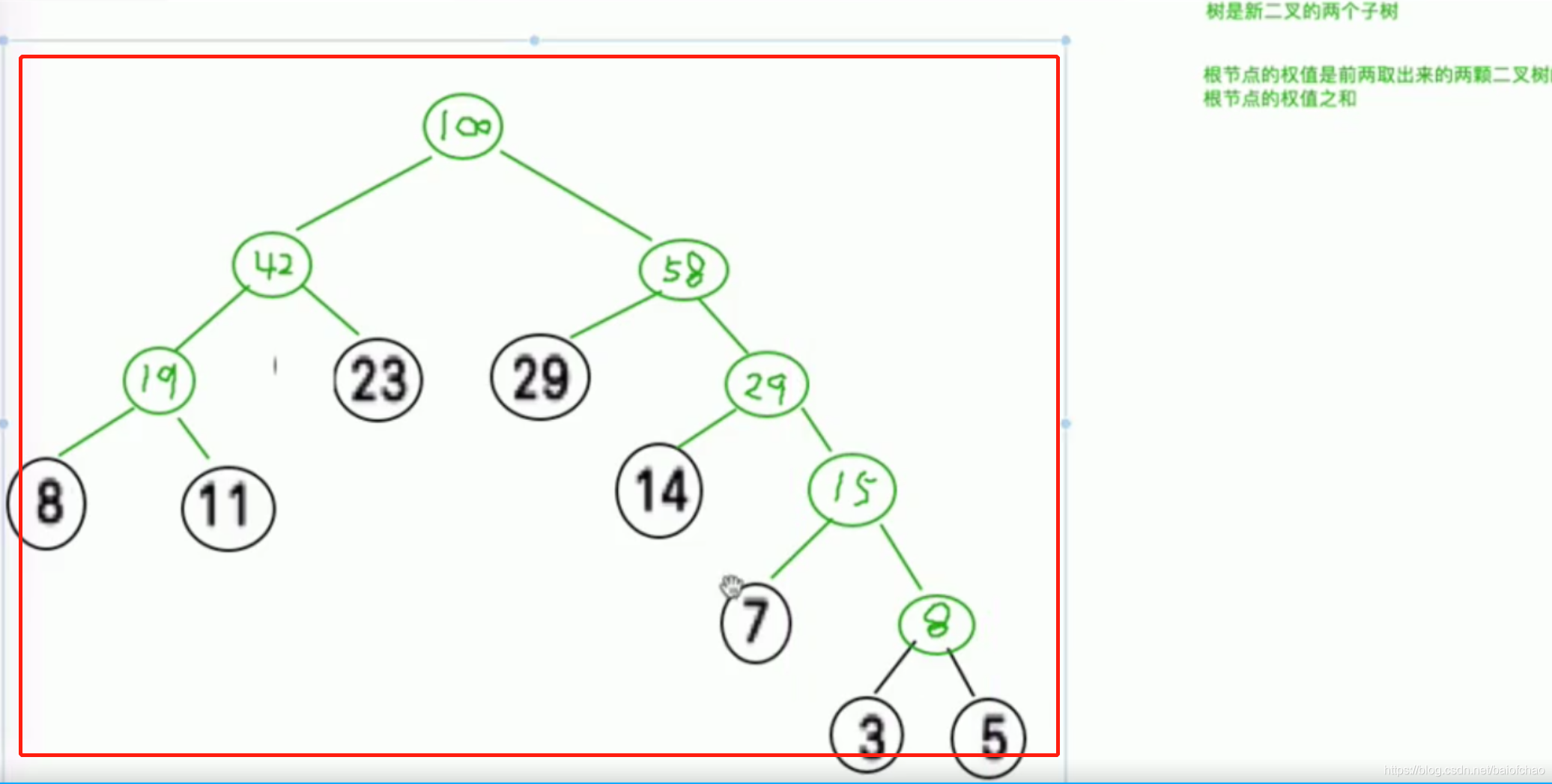
代码实现
- 统计字符数并排序
- 创建赫夫曼树
- 创建赫夫曼编码表
- 编码
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class TestHuffmanTree {
public static void main(String[] args) {
int[] arr = {3,7,8,29,5,11,23,14};
Node node = createHuffmanTree(arr);
System.out.println(node);
}
//创建赫夫曼树
public static Node createHuffmanTree(int[] arr) {
//先使用数组中所有的元素创建若干个二叉树,(只有一个节点)
List<Node> nodes = new ArrayList<>();
for(int value:arr) {
nodes.add(new Node(value));
}
//循环处理,
while(nodes.size()>1) {
//排序
Collections.sort(nodes);
//取出来权值最小的两个二叉树
//取出最权值最小的二叉树
Node left = nodes.get(nodes.size()-1);
//取出最权值次小的二叉树
Node right = nodes.get(nodes.size()-2);
//创建一颗新的二叉树
Node parent = new Node(left.value+right.value);
//把取出来的两个二叉树移除
nodes.remove(left);
nodes.remove(right);
//放入原来的二叉树集合中
nodes.add(parent);
}
return nodes.get(0);
}
}
public class Node implements Comparable<Node> {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public int compareTo(Node o) {
return -(this.value - o.value);
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
}
赫夫曼编码


赫夫曼编码-代码实现
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.OutputStream;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Map.Entry;
public class TestHuffmanCode {
public static void main(String[] args) {
// String msg="can you can a can as a can canner can a can.";
// byte[] bytes = msg.getBytes();
// //进行赫夫曼编码压缩
// byte[] b = huffmanZip(bytes);
// //使用赫夫曼编码进行解码
// byte[] newBytes = decode(huffCodes,b);
// System.out.println(new String(newBytes));
String src="1.bmp";
String dst="2.zip";
// try {
// zipFile(src, dst);
// } catch (IOException e) {
// e.printStackTrace();
// }
try {
unZip("2.zip", "3.bmp");
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* 文件的解压
* @param src
* @param dst
* @throws Exception
*/
public static void unZip(String src,String dst) throws Exception {
//创建一个输入流
InputStream is = new FileInputStream("2.zip");
ObjectInputStream ois = new ObjectInputStream(is);
//读取byte数组
byte[] b = (byte[]) ois.readObject();
//读取赫夫曼编码表
Map<Byte, String> codes = (Map<Byte, String>) ois.readObject();
ois.close();
is.close();
//解码
byte[] bytes = decode(codes, b);
//创建一个输出流
OutputStream os = new FileOutputStream(dst);
//写出数据
os.write(bytes);
os.close();
}
/**
* 压缩文件
* @param src
* @param dst
* @throws IOException
*/
public static void zipFile(String src,String dst) throws IOException {
//创建一个输入流
InputStream is = new FileInputStream(src);
//创建一个和输入流指向的文件大小一样的byte数组
byte[] b = new byte[is.available()];
//读取文件内容
is.read(b);
is.close();
//使用赫夫曼编码进行编码
byte[] byteZip = huffmanZip(b);
//输出流
OutputStream os = new FileOutputStream(dst);
ObjectOutputStream oos = new ObjectOutputStream(os);
//把压缩后的byte数组写入文件
oos.writeObject(byteZip);
//把赫夫曼编码表写入文件
oos.writeObject(huffCodes);
oos.close();
os.close();
}
/**
* 使用指定的赫夫曼编码表进行解码
* @param huffCodes2
* @param b
* @return
*/
private static byte[] decode(Map<Byte, String> huffCodes, byte[] bytes) {
StringBuilder sb = new StringBuilder();
//把byte数组转为一个二进制的字符串
for(int i=0;i<bytes.length;i++) {
byte b = bytes[i];
//是否是最后一个。
boolean flag = (i==bytes.length-1);
sb.append(byteToBitStr(!flag,b));
}
//把字符串按照指定的赫夫曼编码进行解码
//把赫夫曼编码的键值对进行调换
Map<String, Byte> map = new HashMap<>();
for(Map.Entry<Byte, String> entry:huffCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//创建一个集合,用于存byte
List<Byte> list = new ArrayList<>();
//处理字符串
for(int i=0;i<sb.length();) {
int count=1;
boolean flag = true;
Byte b=null;
//截取出一个byte
while(flag) {
String key = sb.substring(i, i+count);
b = map.get(key);
if(b==null) {
count++;
}else {
flag=false;
}
}
list.add(b);
i+=count;
}
//把集合转为数组
byte[] b = new byte[list.size()];
for(int i=0;i<b.length;i++) {
b[i]=list.get(i);
}
return b;
}
private static String byteToBitStr(boolean flag,byte b) {
int temp=b;
if(flag) {
temp|=256;
}
String str = Integer.toBinaryString(temp);
if(flag) {
return str.substring(str.length()-8);
}else {
return str;
}
}
/**
* 进行赫夫曼编码压缩的方法
* @param bytes
* @return
*/
private static byte[] huffmanZip(byte[] bytes) {
//先统计每一个byte出现的次数,并放入一个集合中
List<Node> nodes = getNodes(bytes);
//创建一颗赫夫曼树
Node tree = createHuffmanTree(nodes);
//创建一个赫夫曼编码表
Map<Byte, String> huffCodes = getCodes(tree);
//编码
byte[] b = zip(bytes,huffCodes);
return b;
}
/**
* 进行赫夫曼编码
* @param bytes
* @param huffCodes2
* @return
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffCodes) {
StringBuilder sb = new StringBuilder();
//把需要压缩的byte数组处理成一个二进制的字符串
for(byte b:bytes) {
sb.append(huffCodes.get(b));
}
//定义长度
int len;
if(sb.length()%8==0) {
len=sb.length()/8;
}else {
len=sb.length()/8+1;
}
//用于存储压缩后的byte
byte[] by = new byte[len];
//记录新byte的位置
int index = 0;
for(int i=0;i<sb.length();i+=8) {
String strByte;
if(i+8>sb.length()) {
strByte = sb.substring(i);
}else {
strByte = sb.substring(i, i+8);
}
byte byt = (byte)Integer.parseInt(strByte, 2);
by[index]=byt;
index++;
}
return by;
}
//用于临时存储路径
static StringBuilder sb = new StringBuilder();
//用于存储赫夫曼编码
static Map<Byte, String> huffCodes = new HashMap<>();
/**
* 根据赫夫曼树获取赫夫曼编码
* @param tree
* @return
*/
private static Map<Byte, String> getCodes(Node tree) {
if(tree==null) {
return null;
}
getCodes(tree.left,"0",sb);
getCodes(tree.right,"1",sb);
return huffCodes;
}
private static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
if(node.data==null) {
getCodes(node.left, "0", sb2);
getCodes(node.right, "1", sb2);
}else {
huffCodes.put(node.data, sb2.toString());
}
}
/**
* 创建赫夫曼树
* @param nodes
* @return
*/
private static Node createHuffmanTree(List<Node> nodes) {
while(nodes.size()>1) {
//排序
Collections.sort(nodes);
//取出两个权值最低的二叉树
Node left = nodes.get(nodes.size()-1);
Node right = nodes.get(nodes.size()-2);
//创建一颗新的二叉树
Node parent = new Node(null, left.weight+right.weight);
//把之前取出来的两颗二叉树设置为新创建的二叉树的子树
parent.left=left;
parent.right=right;
//把前面取出来的两颗二叉树删除
nodes.remove(left);
nodes.remove(right);
//把新创建的二叉树放入集合中
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 把byte数组转为node集合
* @param bytes
* @return
*/
private static List<Node> getNodes(byte[] bytes) {
List<Node> nodes = new ArrayList<>();
//存储每一个byte出现了多少次。
Map<Byte, Integer> counts = new HashMap<>();
//统计每一个byte出现的次数
for(byte b:bytes) {
Integer count = counts.get(b);
if(count==null) {
counts.put(b, 1);
}else {
counts.put(b, count+1);
}
}
//把每一个键值对转为一个node对象
for(Map.Entry<Byte, Integer> entry:counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
}
public class Node implements Comparable<Node> {
Byte data;
int weight;
Node left;
Node right;
public Node(Byte data,int weight) {
this.data=data;
this.weight=weight;
}
@Override
public String toString() {
return "Node [data=" + data + ", weight=" + weight + "]";
}
@Override
public int compareTo(Node o) {
return o.weight-this.weight;
}
}
二叉查找树
概念
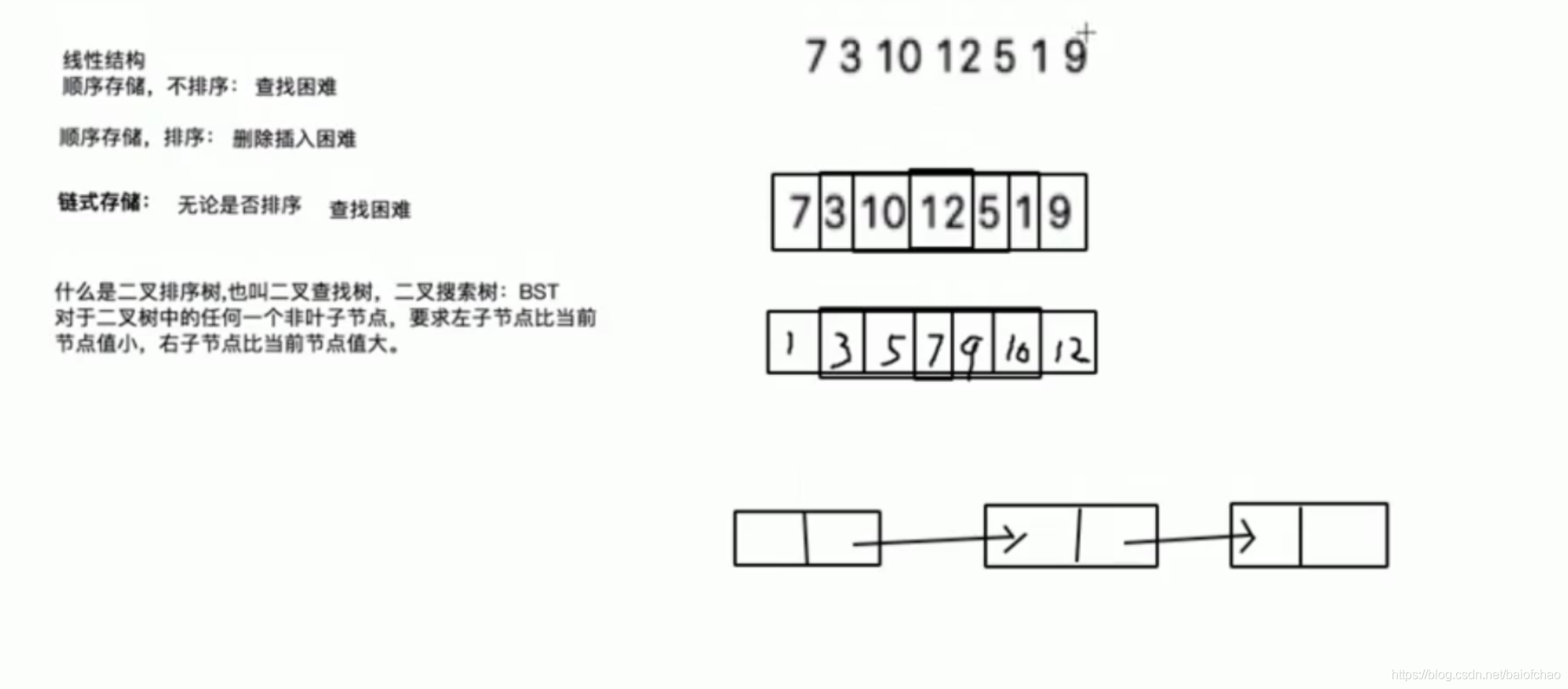
二叉查找树,插入或查找性能都较好
中序遍历二叉查找树,是从小到大的特性
实现
public class BinarySortTree {
Node root;
/**
* 向二叉排序树中添加节点
* @param node
*/
public void add(Node node){
//如果是一颗空树
if(root==null) {
root=node;
}else {
root.add(node);
}
}
/**
* 中序遍历二叉排序树,从小到大的顺序
*/
public void midShow() {
if(root!=null) {
root.midShow(root);
}
}
/**
* 节点的查找
* @param value
* @return
*/
public Node search(int value) {
if(root==null) {
return null;
}else {
return root.search(value);
}
}
/**
* 删除节点
* @param value
*/
public void delete(int value) {
if(root==null) {
return;
}else {
//找到这个节点
Node target = search(value);
//如果没有这个节点
if(target==null) {
return;
}
//找到他的父节点
Node parent = searchParent(value);
//要删除的节点是叶子节点
if(target.left==null&&target.right==null) {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=null;
//要删除的节点是父节点的右子节点
}else {
parent.right=null;
}
//要删除的节点有两个子节点的情况
}else if(target.left!=null&&target.right!=null) {
//删除右子树中值最小的节点,取获取到该节点的值
int min = deleteMin(target.right);
//替换目标节点中的值
target.value=min;
//要删除的节点有一个左子节点或右子节点
}else {
//有左子节点
if(target.left!=null) {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=target.left;
//要删除的节点是父节点的右子节点
}else {
parent.right=target.left;
}
//有右子节点
}else {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=target.right;
//要删除的节点是父节点的右子节点
}else {
parent.right=target.right;
}
}
}
}
}
/**
* 删除一颗树中最小的节点
* @param right
* @return
*/
private int deleteMin(Node node) {
Node target = node;
//递归向左找
while(target.left!=null) {
target=target.left;
}
//删除最小的这个节点
delete(target.value);
return target.value;
}
/**
* 搜索父节点
* @param value
* @return
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}else {
return root.searchParent(value);
}
}
}
AVL树
概念

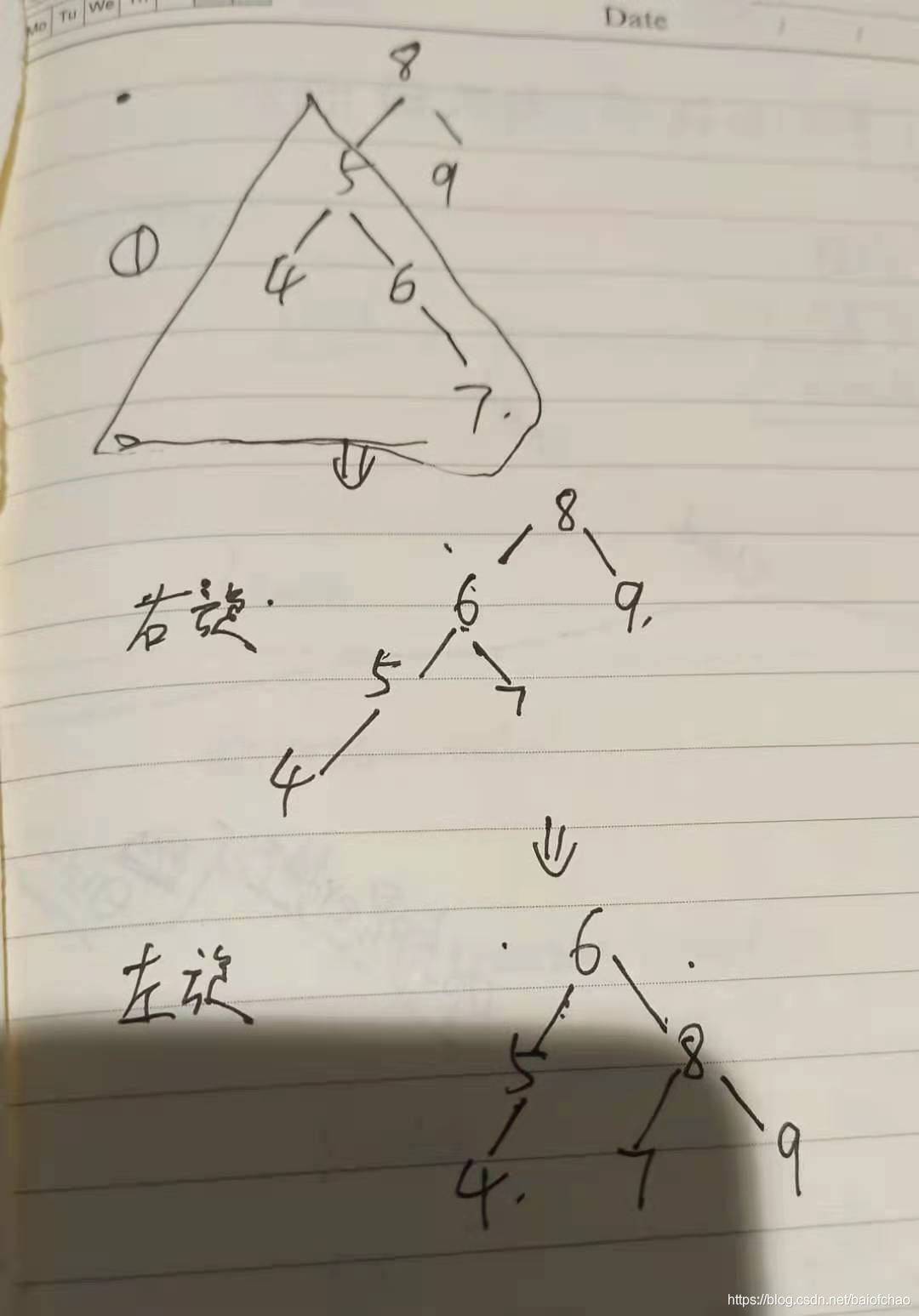
左子树和右子树高度的绝对值不超过1
单旋转:左旋/右旋;
双旋转:左旋/右旋
实现
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value=value;
}
/**
* 返回当前节点的高度
* @return
*/
public int height() {
return Math.max(left==null?0:left.height(), right==null?0:right.height())+1;
}
/**
* 获取左子树的高度
* @return
*/
public int leftHeight() {
if(left==null) {
return 0;
}
return left.height();
}
/**
* 获取右子树的高度
* @return
*/
public int rightHeight() {
if(right==null) {
return 0;
}
return right.height();
}
/**
* 向子树中添加节点
* @param node
*/
public void add(Node node) {
if(node==null) {
return;
}
//判断传入的节点的值比当前子树的根节点的值大还是小
//添加的节点比当前节点的值更小
if(node.value<this.value) {
//如果左节点为空
if(this.left==null) {
this.left=node;
//如果不为空
}else {
this.left.add(node);
}
}else {
if(this.right==null) {
this.right=node;
}else {
this.right.add(node);
}
}
//查询是否平衡
//进行右旋转
if(leftHeight()-rightHeight()>=2) {
//双旋转
if(left!=null&&left.leftHeight()<left.rightHeight()) {
//先左旋转
left.leftRotate();
//再右旋转
rightRotate();
//单旋转
}else {
rightRotate();
}
}
//左旋转
if(leftHeight()-rightHeight()<=-2) {
//双旋转
if(right!=null&&right.rightHeight()<right.leftHeight()) {
right.rightRotate();
leftRotate();
//单旋转
}else {
leftRotate();
}
}
}
/**
* 左旋转
*/
private void leftRotate() {
Node newLeft = new Node(value);
newLeft.left=left;
newLeft.right=right.left;
value=right.value;
right=right.right;
left=newLeft;
}
/**
* 右旋转
*/
private void rightRotate() {
//创建一个新的节点,值等于当前节点的值
Node newRight = new Node(value);
//把新节点的右子树设置了当前节点的右子树
newRight.right=right;
//把新节点的左子树设置为当前节点的左子树的右子树
newRight.left=left.right;
//把当前节点的值换为左子节点的值
value=left.value;
//把当前节点的左子树设置了左子树的左子树
left=left.left;
//把当前节点的右子树设置为新节点
right=newRight;
}
/**
* 中序遍历
* @param node
*/
public void midShow(Node node) {
if(node==null) {
return;
}
midShow(node.left);
System.out.println(node.value);
midShow(node.right);
}
/**
* 查找节点
* @param value2
*/
public Node search(int value) {
if(this.value==value) {
return this;
}else if(value<this.value) {
if(left==null) {
return null;
}
return left.search(value);
}else{
if(right==null) {
return null;
}
return right.search(value);
}
}
/**
* 搜索父节点
* @param value
* @return
*/
public Node searchParent(int value) {
if((this.left!=null&&this.left.value==value)||(this.right!=null&&this.right.value==value)) {
return this;
}else {
if(this.value>value&&this.left!=null) {
return this.left.searchParent(value);
}else if(this.value<value&&this.right!=null){
return this.right.searchParent(value);
}
return null;
}
}
}
public class BinarySortTree {
Node root;
/**
* 向二叉排序树中添加节点
* @param node
*/
public void add(Node node){
//如果是一颗空树
if(root==null) {
root=node;
}else {
root.add(node);
}
}
/**
* 中序遍历二叉排序树,从小到大的顺序
*/
public void midShow() {
if(root!=null) {
root.midShow(root);
}
}
/**
* 节点的查找
* @param value
* @return
*/
public Node search(int value) {
if(root==null) {
return null;
}else {
return root.search(value);
}
}
/**
* 删除节点
* @param value
*/
public void delete(int value) {
if(root==null) {
return;
}else {
//找到这个节点
Node target = search(value);
//如果没有这个节点
if(target==null) {
return;
}
//找到他的父节点
Node parent = searchParent(value);
//要删除的节点是叶子节点
if(target.left==null&&target.right==null) {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=null;
//要删除的节点是父节点的右子节点
}else {
parent.right=null;
}
//要删除的节点有两个子节点的情况
}else if(target.left!=null&&target.right!=null) {
//删除右子树中值最小的节点,取获取到该节点的值
int min = deleteMin(target.right);
//替换目标节点中的值
target.value=min;
//要删除的节点有一个左子节点或右子节点
}else {
//有左子节点
if(target.left!=null) {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=target.left;
//要删除的节点是父节点的右子节点
}else {
parent.right=target.left;
}
//有右子节点
}else {
//要删除的节点是父节点的左子节点
if(parent.left.value==value) {
parent.left=target.right;
//要删除的节点是父节点的右子节点
}else {
parent.right=target.right;
}
}
}
}
}
/**
* 删除一颗树中最小的节点
* @param right
* @return
*/
private int deleteMin(Node node) {
Node target = node;
//递归向左找
while(target.left!=null) {
target=target.left;
}
//删除最小的这个节点
delete(target.value);
return target.value;
}
/**
* 搜索父节点
* @param value
* @return
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}else {
return root.searchParent(value);
}
}
}
public class TestBinarySortTree {
public static void main(String[] args) {
// int[] arr = new int[] {8,9,6,7,5,4};
int[] arr = new int[] {8,9,5,4,6,7};
//创建一颗二叉排序树
BinarySortTree bst = new BinarySortTree();
//循环添加
for(int i:arr) {
bst.add(new Node(i));
}
//查看高度
System.out.println(bst.root.height());
//
System.out.println(bst.root.value);
}
}
多路查找树

2-3树/2-3-4树
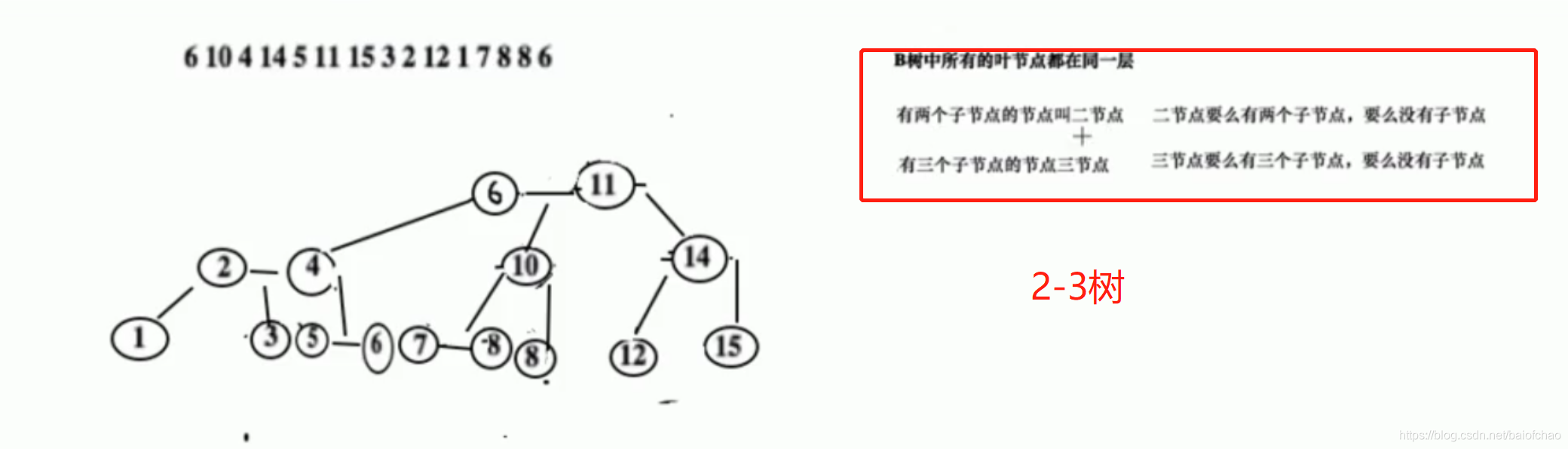
B树
B+树
5. 哈希表
概念
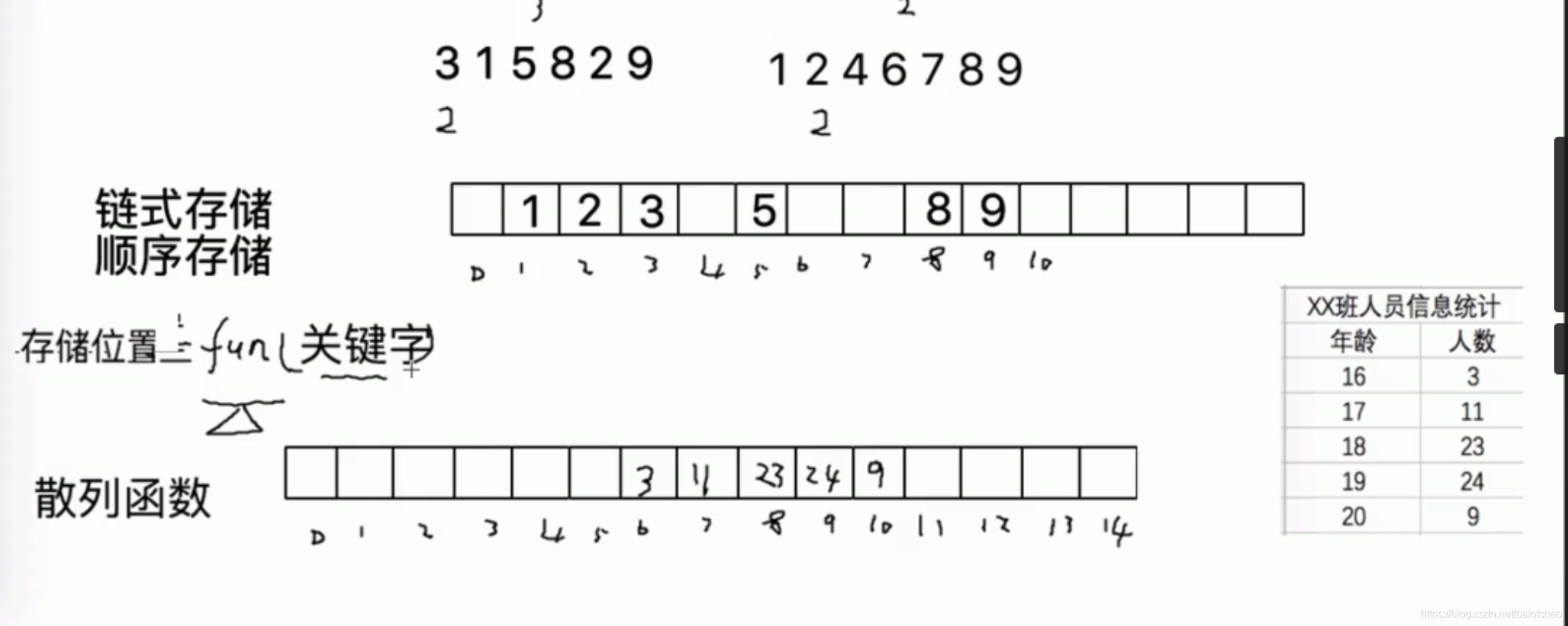
散列函数
- 直接定址法
- 数字分析法
- 平方取中法
- 取余法
- 随机数法
直接定址法-代码实现:
import java.util.Arrays;
public class HashTable {
private StuInfo[] data = new StuInfo[100];
/**
* 向散列表中添加元素
* @param stuInfo
*/
public void put(StuInfo stuInfo) {
//调用散列函数获取存储位置
int index = stuInfo.hashCode();
//添加元素
data[index]=stuInfo;
}
public StuInfo get(StuInfo stuInfo) {
return data[stuInfo.hashCode()];
}
@Override
public String toString() {
return "HashTable [data=" + Arrays.toString(data) + "]";
}
}
public class StuInfo {
private int age;
private int count;
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
/**
* 散列函数
*/
public int hashCode() {
return age;
}
public StuInfo(int age, int count) {
super();
this.age = age;
this.count = count;
}
public StuInfo(int age) {
super();
this.age = age;
}
@Override
public String toString() {
return "StuInfo [age=" + age + ", count=" + count + "]";
}
}
public class TestHashTable {
public static void main(String[] args) {
StuInfo s1 = new StuInfo(16, 3);
StuInfo s2 = new StuInfo(17, 11);
StuInfo s3 = new StuInfo(18, 23);
StuInfo s4 = new StuInfo(19, 24);
StuInfo s5 = new StuInfo(20, 9);
HashTable ht = new HashTable();
ht.put(s1);
ht.put(s2);
ht.put(s3);
ht.put(s4);
ht.put(s5);
System.out.println(ht);
//想要获取的目标数据
StuInfo target = new StuInfo(18);
StuInfo info = ht.get(target);
System.out.println(info);
}
}
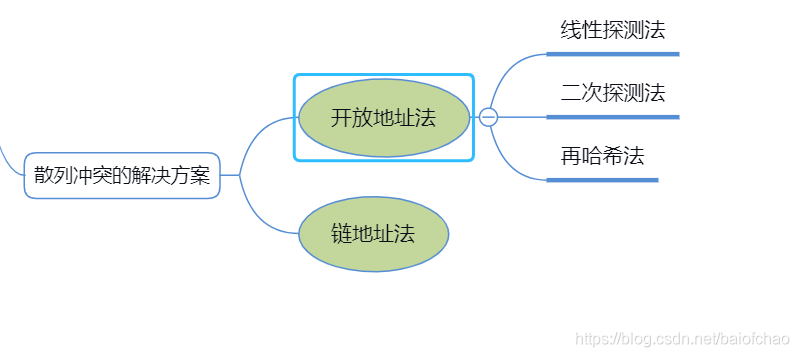
散列冲突解决方案
6. 图
概念
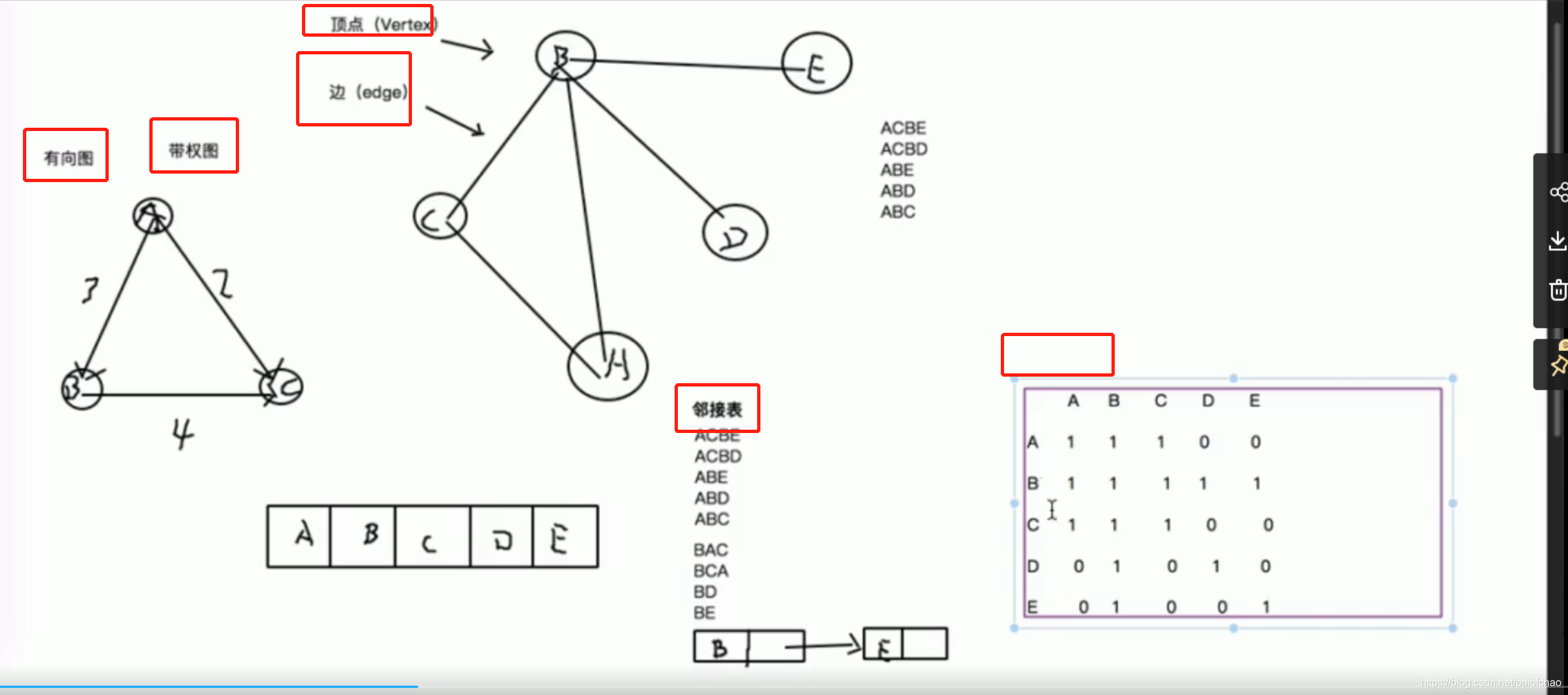
实现
import demo2.MyStack;
/**
* 图
* @author Richard
*
*/
public class Graph {
private Vertex[] vertex;
private int currentSize;
public int[][] adjMat;
private MyStack stack = new MyStack();
//当前遍历的下标
private int currentIndex;
public Graph(int size) {
vertex=new Vertex[size];
adjMat=new int[size][size];
}
/**
* 向图中加入一个顶点
* @param v
*/
public void addVertex(Vertex v) {
vertex[currentSize++]=v;
}
public void addEdge(String v1,String v2) {
//找出两个顶点的下标
int index1=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v1)) {
index1=i;
break;
}
}
int index2=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v2)) {
index2=i;
break;
}
}
adjMat[index1][index2]=1;
adjMat[index2][index1]=1;
}
/**
* 深度优先搜索算法遍历图
*/
public void dfs() {
//把第0个顶点标记为已访问状态
vertex[0].visited=true;
//把第0个顶点的下标。
stack.push(0);
//打印顶点的值
System.out.println(vertex[0].getValue());
//遍历
out:while(!stack.isEmpty()) {
for(int i=currentIndex+1;i<vertex.length;i++) {
//如果和下一个遍历的元素是通的
if(adjMat[currentIndex][i]==1&&vertex[i].visited==false) {
//把下一个元素压入栈中
stack.push(i);
vertex[i].visited=true;
System.out.println(vertex[i].getValue());
continue out;
}
}
//弹出栈顶元素
stack.pop();
//修改当前位置为栈顶元素的位置
if(!stack.isEmpty()) {
currentIndex=stack.peek();
}
}
}
}
import java.util.Arrays;
public class TestGraph {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "C");
g.addEdge("B", "C");
g.addEdge("A", "B");
g.addEdge("B", "D");
g.addEdge("B", "E");
for(int[] a:g.adjMat) {
System.out.println(Arrays.toString(a));
}
//深度优先遍历
g.dfs();
}
}
/**
* 顶点类
* @author Richard
*/
public class Vertex {
private String value;
public boolean visited;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Vertex(String value) {
super();
this.value = value;
}
@Override
public String toString() {
return value;
}
}
public class MyStack {
//栈的底层我们使用数组来存储数据
int[] elements;
public MyStack() {
elements = new int[0];
}
//压入元素
public void push(int element) {
// 创建一个新的数组
int[] newArr = new int[elements.length + 1];
// 把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
// 把添加的元素放入新数组中
newArr[elements.length] = element;
// 使用新数组替换旧数组
elements = newArr;
}
//取出栈顶元素
public int pop() {
//栈中没有元素
if(elements.length==0) {
throw new RuntimeException("stack is empty");
}
//取出数组的最后一个元素
int element = elements[elements.length-1];
//创建一个新的数组
int[] newArr = new int[elements.length-1];
//原数组中除了最后一个元素的其它元素都放入新的数组中
for(int i=0;i<elements.length-1;i++) {
newArr[i]=elements[i];
}
//替换数组
elements=newArr;
//返回栈顶元素
return element;
}
//查看栈顶元素
public int peek() {
//栈中没有元素
if(elements.length==0) {
throw new RuntimeException("stack is empty");
}
return elements[elements.length-1];
}
//判断栈是否为空
public boolean isEmpty() {
return elements.length==0;
}
}
