[NOI2018] 归程
题面:https://www.luogu.com.cn/problem/P4768
题解
具有纪念意义的一道题
AFO之后写的第一道题
5555……竟然写了一个上午,不愧是老年选手
咳咳……回归正题
首先贪心一下,尽量选海拔大的边,于是按海拔建Kruscal最大生成树
先来复习一下Kruscal生成树是什么
回顾Kruscal的算法流程:按照权值大小顺序依次加边,用并查集判断连通性,如果不连通就加入该边。
而Kruscal生成树是在加入一条边的时候,新建一个节点代表这条边,该边连接的两点的祖先向新建的点连边
如图
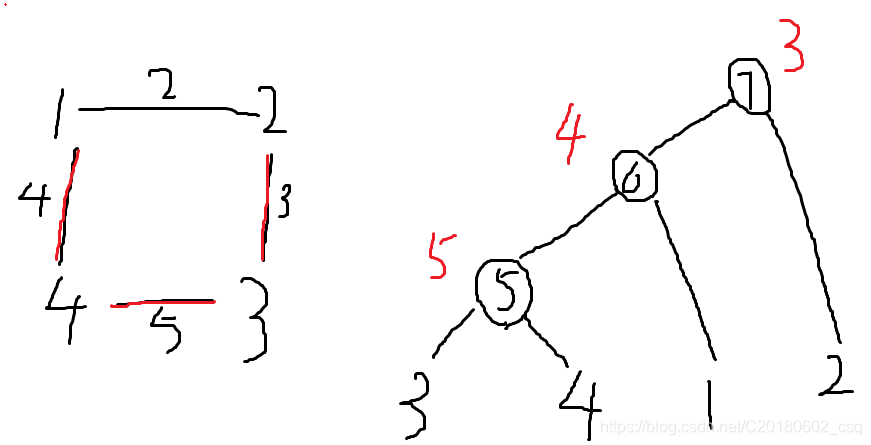
?左图(红色的边为生成树中的边)的Kruscal最大生成树就是右图(红色的数字代表边权)
这个东西有什么用呢?
首先,它(后文默认是最大生成树)有一个性质,就是新建点的权值从下往上依次递减
对于某一个节点u,如果求它只经过权值大于k的边所能到达的点集,这时Kruscal生成树就派上用场啦
从点u一直向上走,走到某一个点的父亲的权值小于k时停止,此时所在点的子树,就是点u所能到达的点集
为什么呢?
其实Kruscal算法中加入的每一条边都是瓶颈边(就是能够连通两个点集的最大/小的边)
在Kruscal生成树上走,就是不断地通过瓶颈边来扩大点集
当走到走不动的时候,就说明此时已经是可到达点集的极限了(因为如果瓶颈边都走不了,其他的边就更过不去了)
好了,返回本题
先跑一个spfa,然后建出Kruscal生成树(边建边统计子树的最小dis值)
回答询问时,利用倍增来爬树,直接输出答案即可
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<deque>
using namespace std;
inline int gi()
{
int num=0,flg=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 200005
#define M 400005
int fir[N*2],to[M*2],cd[M*2],nxt[M*2],cnt;
void adde(int a,int b,int c)
{
to[++cnt]=b;cd[cnt]=c;nxt[cnt]=fir[a];fir[a]=cnt;
to[++cnt]=a;cd[cnt]=c;nxt[cnt]=fir[b];fir[b]=cnt;
}
unsigned int dis[N];bool inq[N];
deque<int> q;
void spfa(int s)
{
memset(dis,0x7f,sizeof(dis));
memset(inq,0,sizeof(inq));
q.push_back(s);inq[s]=1;dis[s]=0;
int u,v,w;
while(!q.empty()){
u=q.front();q.pop_front();
for(int p=fir[u];p;p=nxt[p]){
v=to[p];w=cd[p];
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!inq[v]){
if(!q.empty()&&dis[v]<dis[q.front()])q.push_front(v);
else q.push_back(v);
}
}
}
}
}
struct node{
int u,v,cd,h;
}e[M];
bool cmp(node a,node b){return a.h>b.h;}
#define LOG 18
int fa[N*2],con,f[LOG+2][N*2];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int mi[N*2],hei[N*2];
int main()
{
int T,n,m,Q,K,S,i,j;
T=gi();
while(T--){
cnt=0;memset(fir,0,sizeof(fir));
n=gi();m=gi();
for(i=1;i<=m;i++){
e[i].u=gi();e[i].v=gi();e[i].cd=gi();e[i].h=gi();
adde(e[i].u,e[i].v,e[i].cd);
}
spfa(1);
sort(e+1,e+m+1,cmp);
for(i=1;i<=n;i++)fa[i]=i,mi[i]=dis[i];
con=n;
int ens=0;
for(i=1;i<=m;i++){
int u=find(e[i].u),v=find(e[i].v);
if(u!=v){
fa[++con]=con;
f[0][u]=f[0][v]=con;
fa[u]=fa[v]=con;
mi[con]=min(mi[u],mi[v]);
hei[con]=e[i].h;
if(++ens==n-1)break;
}
}
for(j=1;j<=LOG;j++)
for(i=1;i<=con;i++)
f[j][i]=f[j-1][f[j-1][i]];
Q=gi();K=gi();S=gi();
unsigned int lasans=0;
while(Q--){
int v=(gi()+lasans*K-1)%n+1,h=(gi()+lasans*K)%(S+1);
for(j=LOG;j>=0;j--)
if(hei[f[j][v]]>h)v=f[j][v];
lasans=mi[v];
printf("%d\n",lasans);
}
}
}?
[Ynoi2016] 炸脖龙 I?
题面:https://www.luogu.com.cn/problem/P3934
题解
55555……这是一个黑题变紫,紫题变蓝的时代
它一年前明明时黑题啊,怎么就变紫了
算了,毕竟老年选手已经跟不上时代的节奏
咳咳,回归正题
首先,我们有拓展欧拉定理
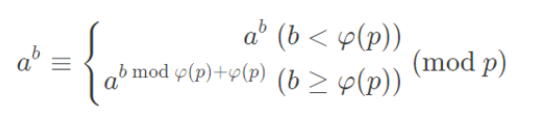
?它揭示了a^b在mod p意义下的规律
大概就是呈现一个rho 的形状(开始没有规律,然后从某一个地方进入循环节,类似混循环小数)
然后,我们发现b mod phi(p)的部分可以递归
当phi(p)=1的时候,递归终止
而对于一个数,对其求log级别次的phi,就会变成1
为什么呢?
考虑phi(x)的定义
若x=(a1^p1)*(a2^p2)*……*(an^pn)? ? ? ? ? ? ? ? ? ? ? ? (ai均为质数)
则phi(x)=((a1-1)*a1^(p1-1))*((a2-1)*a2^(p2-1))*……*((an-1)*an^(pn-1))
=(a1-1)*(a2-1)*……*(an-1)*(a1^(p1-1))*(a2^(p2-1))*……*(an^(pn-1))
此时a1-1,a2-1,……,an-1成为了新的因数(如果ai不是2,则必定可以ai-1分解出一个质因子2)
最终ai-1会分解为2^k*(b1^q1)*(b2^q2)……,其中bi<ai
这些新产生的(bi^qi)有的会加入(aj^(pj-1))中(当bi=aj时),有些就自成一派
我们再来考虑一下,一次phi操作,会使得所有的质因子次数-1,然后在某些质因子上加上一些值
而最坏的情况就是,全部都加在了一个质因子上,导致后续的质因子数减少,一次phi操作的效果削弱,而质因子2就是这样的一个质因子,这就是为什么对一个数连续phi个几次之后,不约而同地变成了2^n的原因(ai-1=2^k*(b1^q1)*(b2^q2)……)
然而,即便是"最坏"情况(其实严格来说不是最坏的),所需的phi操作次数也只有logn次
所以,对于一个数,对其求log级别次的phi,就会变成1
(感觉这个证明也不太严格。。。)
回归正题
我们用差分+树状数组来维护单点值,然后从查询区间的左端点l一个个往后走,走到r或p=1为止
然后递归回来计算答案
注意,由于答案在return的时候已经对p取模了,所以我们还要额外算一个real值,来判断它是否大于p(应该有更简单的方法)
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
inline int gi()
{
char c;int num=0,flg=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 500005
#define LL long long
int n,m;
LL tra[N];
void update(int x,int k){while(x<=n){tra[x]+=k;x+=x&-x;}}
LL getsum(int x){LL sum=0;while(x){sum+=tra[x];x-=x&-x;}return sum;}
#define M 20000001
int pri[1280000],phi[M+5],tot;
bool vis[M];
void shai()
{
int i,j;
vis[1]=phi[1]=1;
for(i=2;i<=M;i++){
if(!vis[i]){
pri[++tot]=i;
phi[i]=i-1;
}
for(j=1;j<=tot;j++){
int tmp=pri[j]*i;
if(tmp>M)break;
vis[tmp]=1;
if(i%pri[j]==0){phi[tmp]=phi[i]*pri[j];break;}
else phi[tmp]=phi[i]*(pri[j]-1);
}
}
}
int l,r;
pair<int,int> ksm(LL x,int y,int p)
{
int ans=1,real=1;LL tmp=min(1ll*M,x);x%=p;
while(y){
if(y&1){ans=1ll*ans*x%p;real=min(1ll*M,1ll*real*tmp);}
y>>=1;x=1ll*x*x%p;tmp=min(1ll*M,1ll*tmp*tmp);
}
return make_pair(ans,real);
}
pair<int,int> euler(int i,int p)
{
if(p==1||i>r) return make_pair(1,1);
pair<int,int> b=euler(i+1,phi[p]);
if(b.second>=phi[p])
return ksm(getsum(i),b.first+phi[p],p);
return ksm(getsum(i),b.first,p);
}
int main()
{
//freopen("P3934_3.in","r",stdin);
//freopen("my.out","w",stdout);
shai();
int i,k,o,p;
n=gi();m=gi();
for(i=1;i<=n;i++){
update(i,k=gi());
update(i+1,-k);
}
for(i=1;i<=m;i++){
o=gi();l=gi();r=gi();p=gi();
if(o==1){update(l,p);update(r+1,-p);}
else{
if(p==1){printf("0\n");continue;}
pair<int,int> ans=euler(l,p);
printf("%d\n",ans.first);
}
}
}Rmq Problem / mex
题面:https://www.luogu.com.cn/problem/P4137
题解
可持久化线段树模板复习
想了想,也可以莫队+值域分块(O(n*sqrt(m)+m*sqrt(n)))
具体一点
就是可持久化线段树维护时间戳,通过时间戳的最小值是否小于l来判断该区间是否可行
注意数组要开大一点
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
inline int gi()
{
int num=0,flg=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 200005
#define LOG 19
struct node{
int l,r,x;
}a[N*LOG];
int T[N],tot;
void pushup(int i)
{
a[i].x=min(a[a[i].l].x,a[a[i].r].x);
}
void insert(int &rt,int pre,int l,int r,int p,int tim)
{
rt=++tot;
a[rt]=a[pre];
if(l==r){a[rt].x=tim;return;}
int mid=(l+r)>>1;
if(p<=mid){
insert(a[rt].l,a[pre].l,l,mid,p,tim);
pushup(rt);
}
else{
insert(a[rt].r,a[pre].r,mid+1,r,p,tim);
pushup(rt);
}
}
int ans,ql,qr;
void query(int i,int l,int r)
{
if(!i||l==r){ans=l;return;}
if(a[a[i].l].x<ql)query(a[i].l,l,(l+r)>>1);
else query(a[i].r,((l+r)>>1)+1,r);
}
int main()
{
int n,m,i,x;
n=gi();m=gi();
for(i=1;i<=n;i++){
x=gi();
insert(T[i],T[i-1],0,N,x,i);
}
for(i=1;i<=m;i++){
ans=0;ql=gi();qr=gi();
query(T[qr],0,N);
printf("%d\n",ans);
}
}[Ynoi2016] 这是我自己的发明
题面:https://www.luogu.com.cn/problem/P4689
题解
写了一下午,调了一晚上
先用dfs序把树转成平面,于是就变成了求两个区间中相同的数有多少对
由于具有可加性,于是我们对问题进行差分
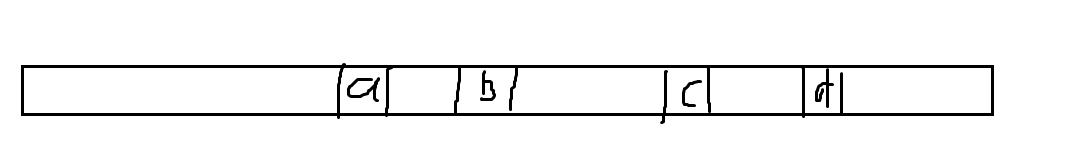
?(a,b,c,d)=(1,b,1,d)-(1,a,1,d)-(1,b,1,c)+(1,a,1,c)
于是就把四个端点的莫队消成了两个端点的莫队
在考虑换根操作,发现它只是改变了查询区间的形状
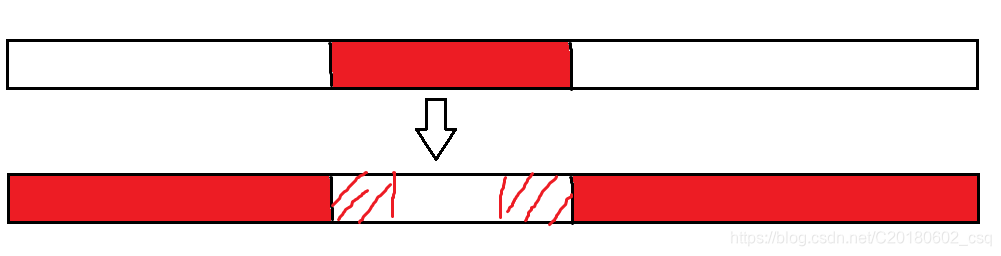
注意,中间挖掉的那一块是root到节点u所经过的u的儿子的子树的区间
这个可以利用倍增快速求出
我们发现,一个询问最多会被拆成9个,直接sort会很慢
于是我们选择基数排序(鸡排)
我写的是分类sort+桶排,应该多了个n*sqrt(n)
接下来就是喜闻乐见的莫队
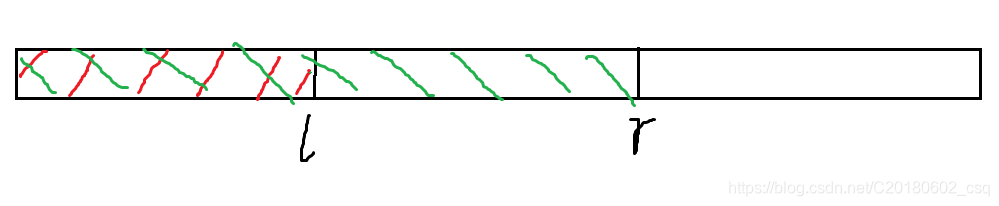
注意,这里的莫队与之前的区间莫队不太一样
两个端点维护的都是前缀值
?
然后,就是一大堆细节
本来拆分询问的时候要分九种类
但是有一个巧妙的方法回避了分类(详见代码)
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
inline int gi()
{
int num=0,flg=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
//part 1
#define N 100005
#define LOG 16
#define M 500005
int hh[N],arr[N];
int to[2*N],nxt[2*N],fir[2*N],cnt;
void adde(int a,int b){to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;}
int f[LOG+2][N],dep[N],siz[N],dfn[N],dc;
void dfs(int u,int fa)
{
dfn[u]=++dc;
f[0][u]=fa;dep[u]=dep[fa]+1;siz[u]=1;
for(int v,p=fir[u];p;p=nxt[p]){
v=to[p];if(v==fa)continue;
dfs(v,u);siz[u]+=siz[v];
}
}
int lg[N];
int pd(int rt,int u)
{
if(dep[rt]<=dep[u]&&rt!=u)return 0;
if(rt==u)return -1;
int x=rt,dis=dep[rt]-dep[u]-1,tmp;
for(;dis;dis^=tmp){
tmp=dis^(dis-1);
tmp=tmp^(tmp>>1);
x=f[lg[tmp]][x];
}
if(f[0][x]==u)return x;
return 0;
}
struct node{
int l,r,id,flg;
node(){}
node(int a,int b,int c,int d){l=a,r=b,id=c,flg=d;}
}q[9*M];
int qcnt,tot;
inline void add(int l,int r,int id,int flg)
{
if(l>r)swap(l,r);
q[++qcnt]=node(l,r,id,flg);
}
inline int sig(int x){return (x&1)?-1:1;}
//part 2
#define C 5000
#define D 300
vector<int> tong1[N/D+5],tong2[N];
bool cmp1(int a,int b){return q[a].r<q[b].r;}
bool cmp2(int a,int b){return q[a].r>q[b].r;}
inline int bel(int i){return i/D+1;}
int res[9*M];
//part 3
int ta[N],tb[N];
long long ans[M];
int main()
{
//part 1
int n,m,i,j,u,v;
n=gi();m=gi();
for(i=1;i<=n;i++)hh[i]=arr[i]=gi();
sort(hh+1,hh+n+1);
int len=unique(hh+1,hh+n+1)-hh-1;
for(i=1;i<=n;i++)arr[i]=lower_bound(hh+1,hh+len+1,arr[i])-hh;
for(i=1;i<n;i++){u=gi();v=gi();adde(u,v);adde(v,u);}
dfs(1,0);
lg[1]=0;
for(j=1;j<=LOG;j++){
lg[1<<j]=j;
for(i=1;i<=n;i++)
f[j][i]=f[j-1][f[j-1][i]];
}
int o,rt=1;
while(m--){
o=gi();
if(o==1)rt=gi();
else{
++tot;
u=gi();v=gi();
int tmp1=pd(rt,u);
int tmp2=pd(rt,v);
int a[3]={0},b[3]={0};
if(tmp1==-1)a[0]=n;
else if(tmp1==0)a[0]=dfn[u]+siz[u]-1,a[1]=dfn[u]-1;//(+-)
else a[0]=dfn[tmp1]-1,a[1]=dfn[tmp1]+siz[tmp1]-1,a[2]=n;//(+-+)
if(tmp2==-1)b[0]=n;
else if(tmp2==0)b[0]=dfn[v]+siz[v]-1,b[1]=dfn[v]-1;
else b[0]=dfn[tmp2]-1,b[1]=dfn[tmp2]+siz[tmp2]-1,b[2]=n;
for(i=0;i<=2&&a[i];i++)
for(j=0;j<=2&&b[j];j++)
add(a[i],b[j],tot,sig(i)*sig(j));
}
}
//part 2
for(i=1;i<=qcnt;i++)
tong1[bel(q[i].l)].push_back(i);
int rcnt=0;
for(i=1;i<=bel(n);i++){
int nn=tong1[i].size();
if(!nn)continue;
if(nn<=C){
if(i&1)sort(tong1[i].begin(),tong1[i].end(),cmp1);
else sort(tong1[i].begin(),tong1[i].end(),cmp2);
for(j=0;j<nn;j++)
res[++rcnt]=tong1[i][j];
}
else{
for(j=0;j<nn;j++){
int tmp=tong1[i][j];
tong2[q[tmp].r].push_back(tmp);
}
if(i&1){
for(j=1;j<=n;j++){
for(int k=tong2[j].size()-1;k>=0;k--)
res[++rcnt]=tong2[j][k];
tong2[j].clear();
}
}
else{
for(j=n;j>=1;j--){
for(int k=tong2[j].size()-1;k>=0;k--)
res[++rcnt]=tong2[j][k];
tong2[j].clear();
}
}
}
}
//part 3
int l=0,r=0,ql,qr;
long long sum=0;
for(i=1;i<=n;i++)
hh[dfn[i]]=arr[i];
for(j=1;j<=qcnt;j++){//A strange mo dui
i=res[j];
ql=q[i].l,qr=q[i].r;
while(l<ql)l++,sum+=1ll*tb[hh[l]],ta[hh[l]]++;
while(r<qr)r++,sum+=1ll*ta[hh[r]],tb[hh[r]]++;
while(l>ql)sum-=1ll*tb[hh[l]],ta[hh[l]]--,l--;
while(r>qr)sum-=1ll*ta[hh[r]],tb[hh[r]]--,r--;
ans[q[i].id]+=1ll*q[i].flg*sum;
}
for(i=1;i<=tot;i++)
printf("%lld\n",ans[i]);
}