????????给定一个?完美二叉树?,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}????????填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为?NULL。
初始状态下,所有?next 指针都被设置为?NULL。
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
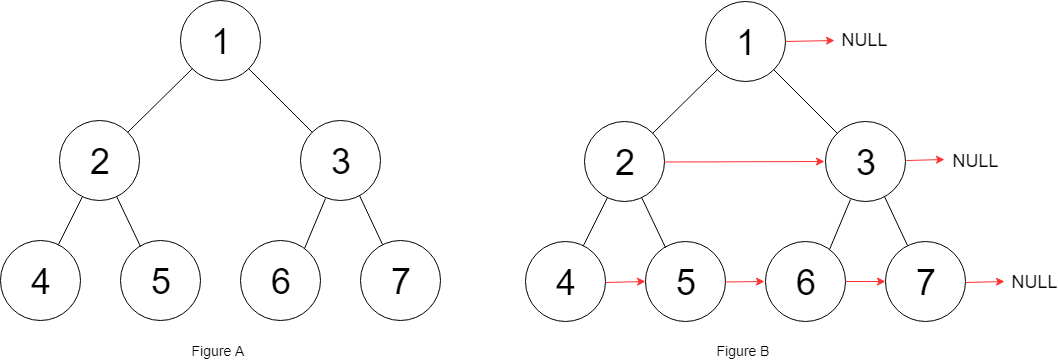
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
提示:
- 树中节点的数量少于?
4096 -1000 <= node.val <= 1000
方法一:层次遍历
????????题目要求将二叉树的每一层节点都连接起来形成一个链表。直观的做法可以对二叉树进行层次遍历,在层次遍历的过程中将二叉树每一层的节点拿出来遍历并连接。
????????层次遍历基于广度优先搜索(BFS),与广度优先搜索的不同之处在于,广度优先搜索每次只会取出一个节点来拓展,而层次遍历会每次将队列中的所有元素都拿出来拓展,这样能保证每次从队列中拿出来遍历的元素都是属于同一层的,可以在遍历的过程中修改每个节点的 next 指针,同时拓展下一层的新队列。
复杂度分析
- 时间复杂度:O(N)。每个节点会被访问一次且只会被访问一次,即从队列中弹出,并建立 next 指针。
- 空间复杂度:O(N)。这是一棵完美二叉树,它的最后一个层级包含 N/2 个节点。广度优先遍历的复杂度取决于一个层级上的最大元素数量。这种情况下空间复杂度为 O(N)。
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
// 初始化队列同时将第一层节点加入队列中,即根节点
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
// 外层的 while 循环迭代的是层数
while (!queue.isEmpty()) {
// 记录当前队列大小
int size = queue.size();
// 遍历这一层的所有节点
for (int i = 0; i < size; i++) {
// 从队首取出元素
Node node = queue.poll();
// 连接
if (i < size - 1) {
node.next = queue.peek();
}
// 拓展下一层节点
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
// 返回根节点
return root;
}
}方法二:使用已建立的 next?指针
思路
- 一棵树中,存在两种类型的?\text{next}next?指针。
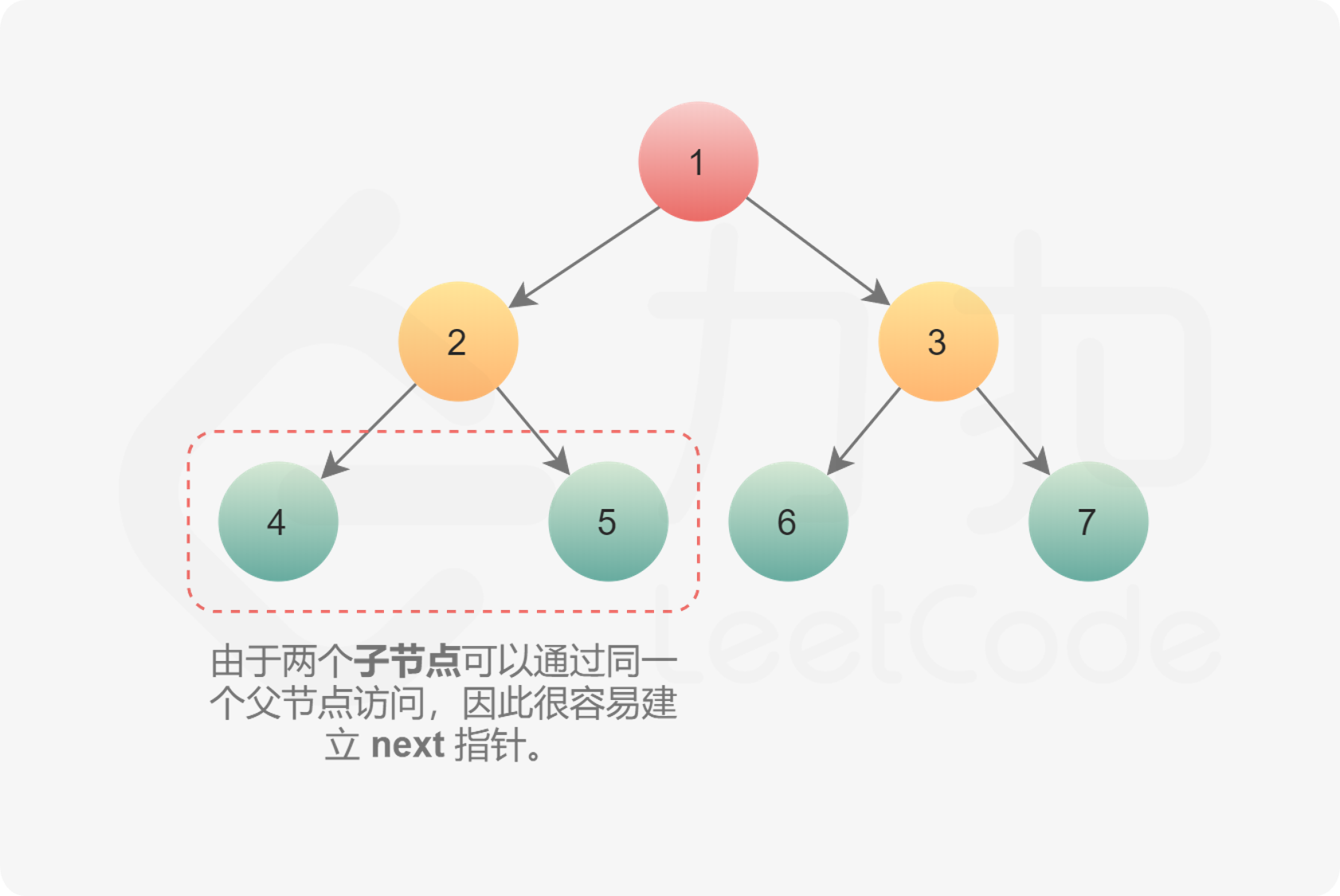
- 第一种情况是连接同一个父节点的两个子节点。它们可以通过同一个节点直接访问到,因此执行下面操作即可完成连接。
node.left.next = node.right
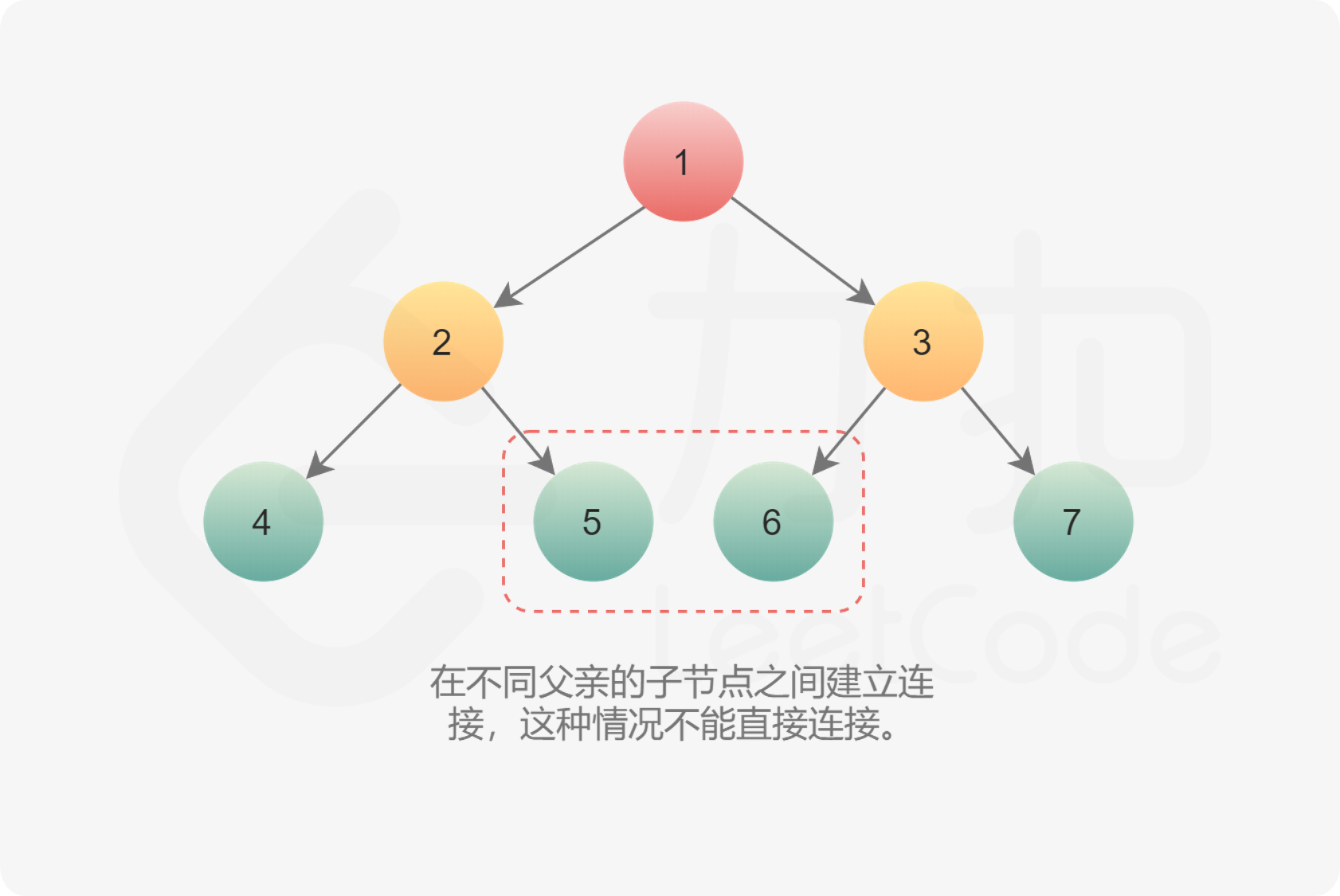
- 第二种情况在不同父亲的子节点之间建立连接,这种情况不能直接连接。
????????如果每个节点有指向父节点的指针,可以通过该指针找到?\text{next}next?节点。如果不存在该指针,则按照下面思路建立连接:
????????第?N?层节点之间建立next?指针后,再建立第N+1?层节点的next?指针。可以通过 next?指针访问同一层的所有节点,因此可以使用第?N?层的 next?指针,为第 N+1?层节点建立 next?指针。
算法
从根节点开始,由于第?0?层只有一个节点,所以不需要连接,直接为第?1?层节点建立 next?指针即可。该算法中需要注意的一点是,当我们为第?N?层节点建立 next?指针时,处于第?N-1 层。当第?N?层节点的 next?指针全部建立完成后,移至第?N?层,建立第N+1?层节点的 next?指针。
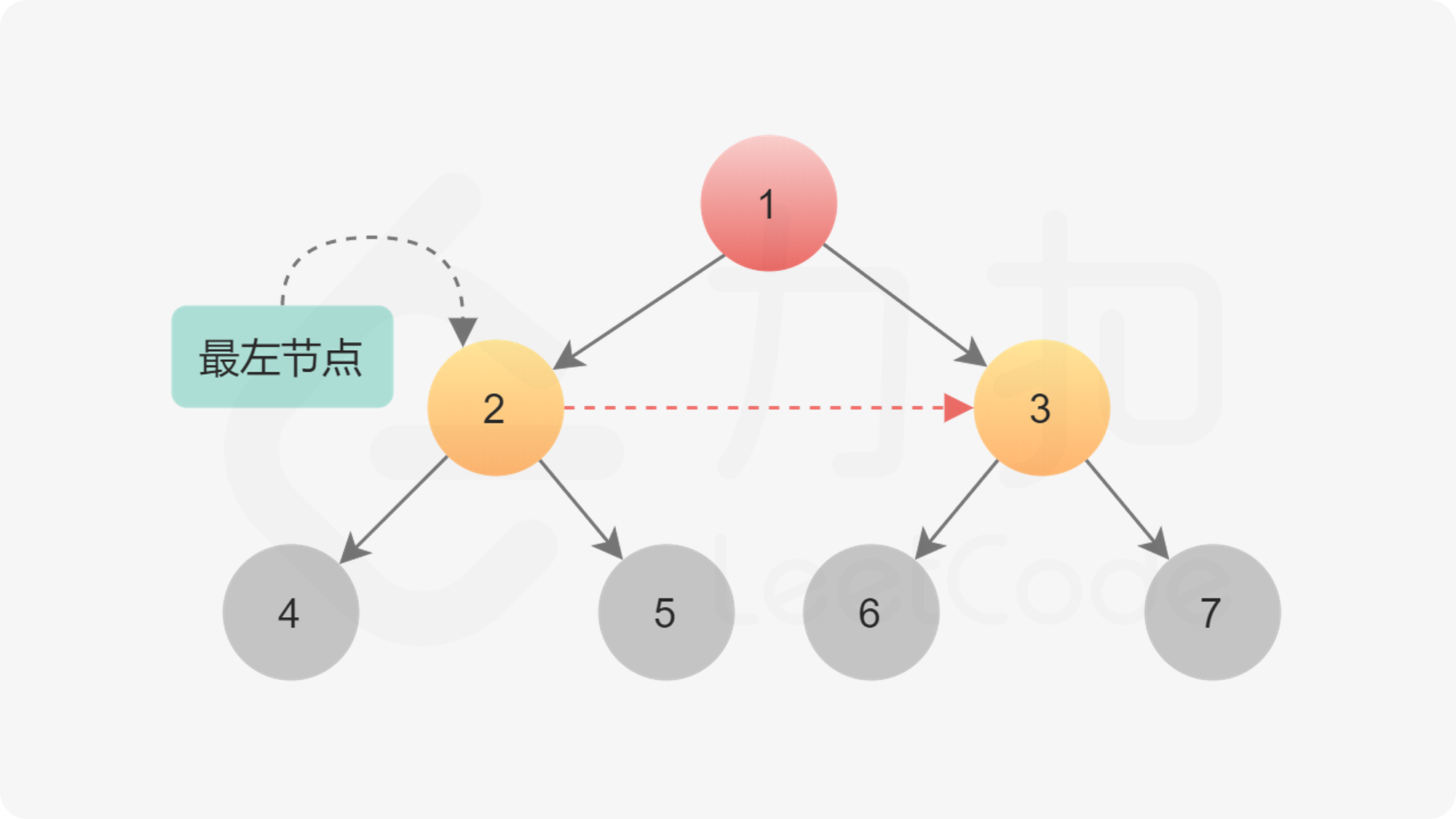
遍历某一层的节点时,这层节点的 next?指针已经建立。只需要知道这一层的最左节点,就可以按照链表方式遍历,不需要使用队列。
上面思路的伪代码如下:
leftmost = root while (leftmost.left != null) { head = leftmost while (head.next != null) { 1) Establish Connection 1 2) Establish Connection 2 using next pointers head = head.next } leftmost = leftmost.left }
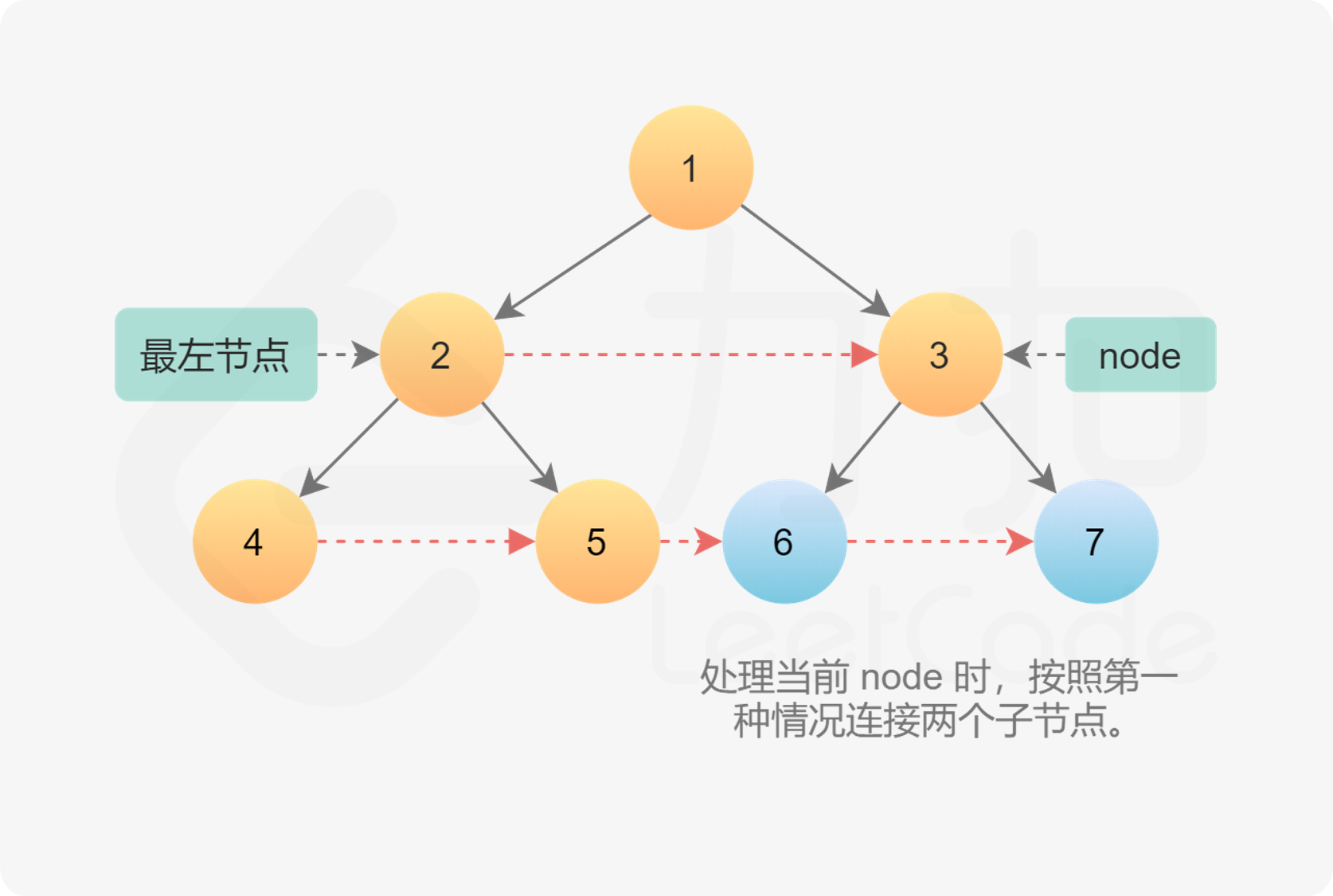
两种类型的 next?指针。
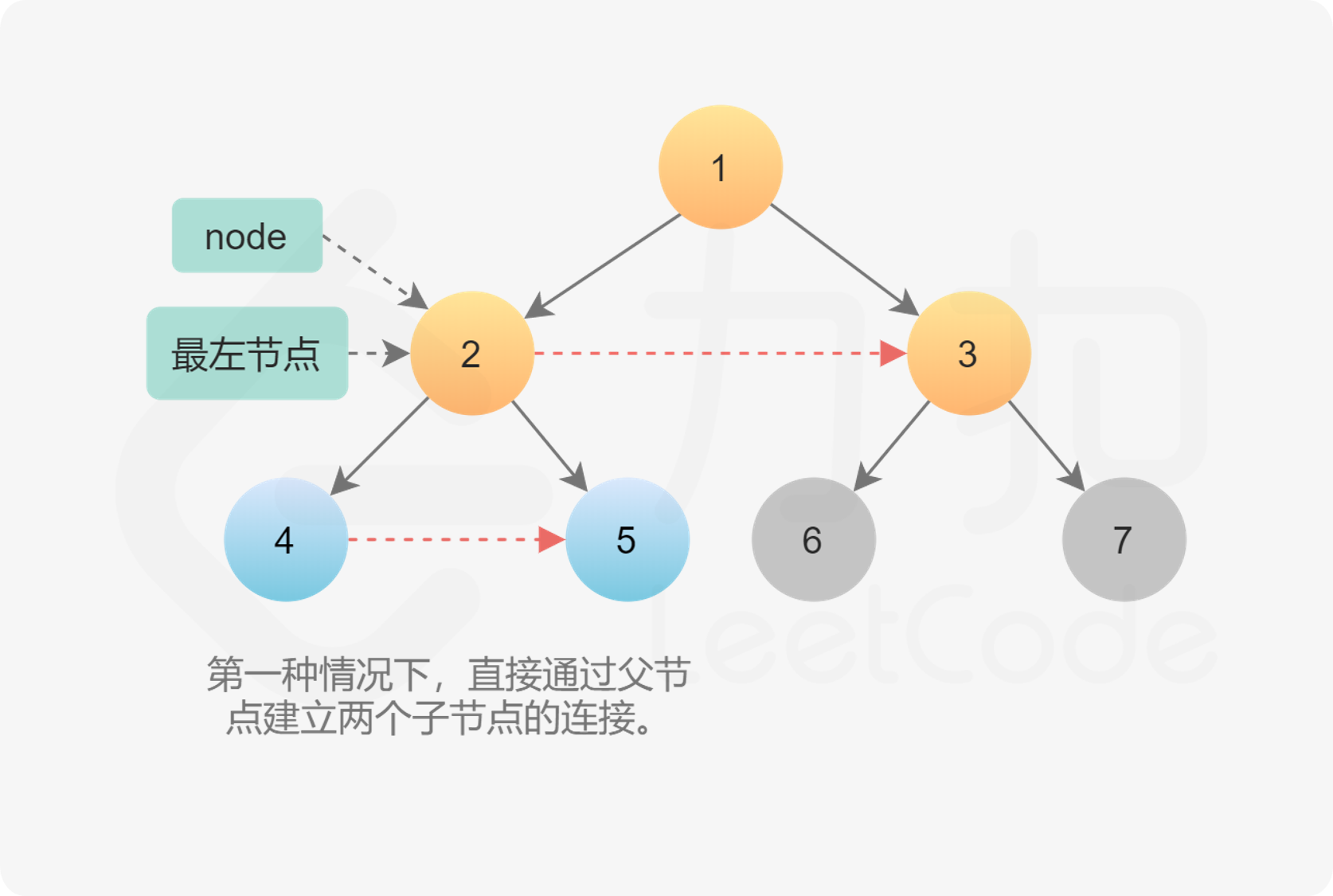
第一种情况两个子节点属于同一个父节点,因此直接通过父节点建立两个子节点的 next?指针即可。
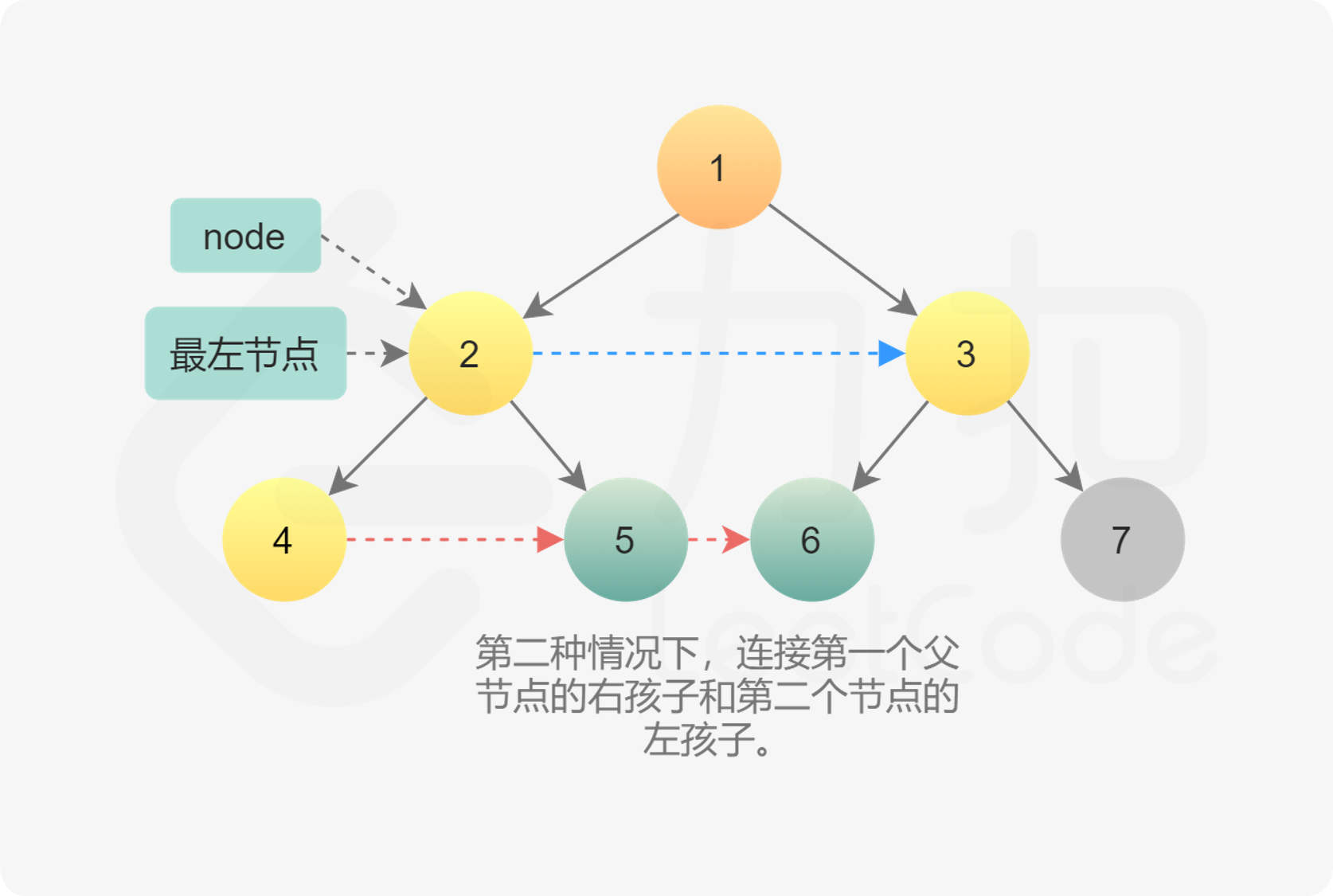
node.left.next = node.right第二种情况是连接不同父节点之间子节点的情况。更具体地说,连接的是第一个父节点的右孩子和第二父节点的左孩子。由于已经在父节点这一层建立了next?指针,因此可以直接通过第一个父节点的 next?指针找到第二个父节点,然后在它们的孩子之间建立连接。
node.right.next = node.next.left完成当前层的连接后,进入下一层重复操作,直到所有的节点全部连接。进入下一层后需要更新最左节点,然后从新的最左节点开始遍历该层所有节点。因为是完美二叉树,因此最左节点一定是当前层最左节点的左孩子。如果当前最左节点的左孩子不存在,说明已经到达该树的最后一层,完成了所有节点的连接。
复杂度分析
- 时间复杂度:O(N),每个节点只访问一次。
- 空间复杂度:O(1),不需要存储额外的节点。
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
// 使用指针之间的关系,从根节点开始
Node leftFirst = root;
// 完美二叉树,最左节点一定是当前层最左节点的左孩子。
// 如果当前最左节点的左孩子不存在,说明已经到达该树的最后一层,完成了所有节点的连接。
while(leftFirst.left != null){
// 遍历这层节点组成的链表,为下一层的节点更新next指针
Node node = leftFirst;
while(node != null){
// 第一个连接
node.left.next = node.right;
// 下一层的连接
if(node.next != null){
node.right.next = node.next.left;
}
// 指针向后移动
node = node.next;
}
// 前往下一层的最左节点
leftFirst = leftFirst.left;
}
// 返回根节点
return root;
}
}// 递归版本代码
class Solution {
public Node connect(Node root) {
// 判定合法性
if(root==null) return null;
// 根节点开始
connection(root);
return root;
}
// 递归主体
public void connection(Node root){
// 通过判断是否是最左侧的元素为null返回
if(root.left == null) return;
// 相同父节点连接操作
root.left.next=root.right;
// 不同父节点连接操作
if(root.next != null){
root.right.next=root.next.left;
}
// 分别左右
connection(root.left);
connection(root.right);
}
}