与树有关的术语:
节点深度:对任意节点x,x节点的深度表示为根节点到x节点的路径长度。所以根节点深度为0,第二层节点深度为1,以此类推
节点高度:对任意节点x,叶子节点到x节点的路径长度就是节点x的高度
树的深度:一棵树中节点的最大深度就是树的深度,也称为高度
父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
子节点:一个节点含有的子树的根节点称为该节点的子节点
节点的层次:从根节点开始,根节点为第一层,根的子节点为第二层,以此类推
兄弟节点:拥有共同父节点的节点互称为兄弟节点
节点的度:节点的子树数目就是节点的度(degree)
叶子节点:度为零的节点就是叶子节点
祖先:对任意节点x,从根节点到节点x的所有节点都是x的祖先(节点x也是自己的祖先)
后代:对任意节点x,从节点x到叶子节点的所有节点都是x的后代(节点x也是自己的后代)
森林:m颗互不相交的树构成的集合就是森林
? 注:其实对于祖先和后代的定义,不同的资料有不同的解释,争论在于节点本身是否是本身的祖先或者后代,我这里的定义取得是《数据结构与算法( Java 描述)-邓俊辉》。维基百科中对于祖先和后代的定义是:
Descendant:A node reachable by repeated proceeding from parent to child.
Ancestor:A node reachable by repeated proceeding from child to parent.
树的种类:
-
无序树: 树的任意节点的子节点没有顺序关系
-
有序树:树的任意节点的子节点有顺序关系
-
二叉树:树的任意节点至多包含两棵子树
-
满二叉树:叶子节点都在同一层并且除叶子节点外的所有节点都有两个子节点

-
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除第d层外的所有节点构成满二叉树,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树

-
平衡二叉树(AVL):它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,同时,平衡二叉树必定是二叉搜索树
-
排序二叉树(二叉搜索树、二叉查找树、BST):是一种特殊结构的二叉树,通过它可以非常方便底对树中的所有节点进行排序和检索,排序二叉树要么是一棵空二叉树,要么是具有下列性质的二叉树
-
若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
-
若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
-
它的左、右子树也分别为排序二叉树;

任意节点的没有键值相等的节点。
-
-
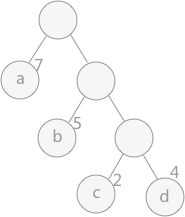
哈夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树。哈夫曼树是二叉树的一种应用,在信息检索中很常用。在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
介绍下一些相关概念:
- 路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图中,从根结点到结点 a 之间的通路就是一条路径。
- 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图中从根结点到结点 c 的路径长度为 3。
- 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图中结点 a 的权为 7,结点 b 的权为 5。
- 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
-
红黑树:虽然排序二叉树可以快速检索,但在最坏的情况下,如果插入的节点集本身就是有序的,要么是由小到大排列,要么是由大到小排列,那么最后得到的排序二叉树将变成链表:所有节点只有左节点或者所有得节点只有右节点,此时得检索效率就会很低。为了改变排序二叉树存在得不足,Rudolf Bayerr于1972年发明了另一种改进后的排序二叉树------红黑树,红黑树是一颗特殊的排序二叉树,红黑树在原有的排序二叉树上增加了如下几个要求:
- 性质1:每个节点要么是红色,要么是黑色;
- 性质2:根节点永远是黑色的;
- 性质3:所有的叶子节点都是空姐点(即null),并且都是黑色的;
- 性质4:每个红色节点的两个子节点都是黑色的。(从每个叶子到根的路径上不会有两个连续的红色节点。)
- 性质5:从任一节点到其子树中每个叶子节点的路径都包含相同数量黑色节点。

? 根据“性质5”,红黑树从根节点到每个叶子节点的路径都包含相同数量的黑色节点,因此从根节点到叶子节点的路径中包含的黑色节点数被称为树的“黑色高度(black-height)”。
? “性质4”则保证了从根节点到叶子节点的最长路径的长度不会超过任何其他路径的2倍。假如有一棵黑色高度为3的红黑树,从根节点到叶子节点的最短路径长度是2,该路径上全是黑色节点(黑色节点----黑色节点----黑色节点)。最长路径也只可能为4,在每个黑色节点之间插入一 个红色节点(黑色节点----红色节点----黑色节点----红色节点----黑色节点), “性质4”保证绝不可能插入更多的红色节点。由此可见,红黑树中最长的路径就是一条红黑交 替的路径。
? 由此可以得出结论:对于给定的黑色高度为N的红黑树,从根到叶子节点的最短路径长度为N-1, 最长路径长度为2*(N- 1)。
? 红黑树通过上面这种限制来保证它大致是平衡的----因为红黑树的高度不会无限增高,这样能保证红黑树在最坏的情况下都是高效的,不会出现普通排序二叉树的情况。
? 由于红黑树知识一棵特殊的排序二叉树,因此对红黑树上的只读操作与普通排序二叉树上的只读操作完全相同,知识红黑树保证了大致平衡,因此检索性能更好。
? 但在红黑树进行插入操作和删除操作会导致树不在符合红黑树的特征,一次插入操作和删除操作都需要进行一定的维护,以保证插入节点、删除节点后的树依然是红黑树。