F - Tickets
题意:给定一个由六个数字组成的字符串数字,前三个字符数字的和与后三个字符数字的和做差取绝对值——key,称它每一个数字的幸运值。询问n次,问从1到当前这个数字,存在多少个比这个数字小且幸运值比当前这个数字小的数字。
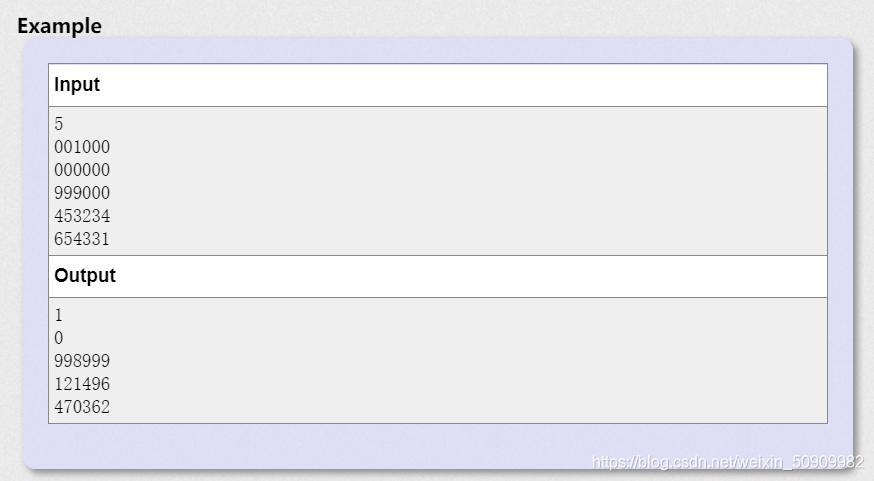
*一开始并没有考虑这道题的数据量问题,直接枚举每一位然后找答案,发现会超时。想到预处理了,但根本不知道如何存下来,在枚举的过程中的状态并不是很好存下来。看了题解才发现这个题原来是DP。 *
思路:这道题不说完全是个DP题,也至少用到了滚动数组的思路。
我们从小到大枚举,边枚举边更新答案,因为每个数都和某个幸运值一一对应,我们可以存下当前这个数的幸运值,然后从小到大枚举所有的幸运值,这里所有的幸运值并不是所有,因为从小到大枚举,所有当前的幸运值都来自于比当前的数小的数——滚动思想。所以把这些数字求和就是这个数字的答案,再开个数组记下来。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
using namespace std;
int a[1000010];
int dp[110];
int main()
{
int i,j,k,x,y,n,m;
memset(dp,0,sizeof(dp));
for(i=0; i<1000000; i++)
{
a[i]=0;x=0;y=0;
x+=i/100000;x+=(i/10000)%10;x+=(i/1000)%10;
y+=(i/100)%10;y+=(i/10)%10;y+=i%10;
k=abs(x-y);
dp[k]++;//存下每种幸运的数量。
for(j = 0; j < k; j++)
a[i]+=dp[j];//遍历比它小的数且幸运值比它低的数字。
}
scanf("%d",&n);
while(n--)
{
scanf("%d",&m);
printf("%d\n",a[m]);
}
return 0;
}
C - Bacteria
题意:n个元素,权值相同的元素可以直接合并,如果权值不同可以去商店里购买任意大小权值的元素,再去合并,我们希望在购买次数较少的情况下,使最后的集合合并为一个元素,如果无论多少次都无法完成最终合并就输出-1,否则输出购买次数。

思路:维护小根堆。为什么要想到先处理最小的元素呢。第一点,比如给一个序列
Y
=
[
3
,
6
]
Y= [3,6]
Y=[3,6],我们希望购买次数少,那么显然就买一个
3
3
3,然后就可以完成两两合并了
!
!
!,我们不可能先去买一个
6
6
6,把后边合并之后,然后再由
Y
=
[
3
,
12
]
Y= [3,12]
Y=[3,12] 这个序列再买
3
3
3,买
6
6
6再去合并为一个集合——除非你傻 。第二点,如果堆顶两个元素无法转化至合并,这两个元素与任意元素合并任意次后仍然相对无法合并。(转化指堆顶整除次堆顶且次堆顶可以由堆顶合并若干次得到)比如
Y
=
[
3
,
7
,
9
]
Y= [3,7,9]
Y=[3,7,9], 因为每次只能合并相同大小的元素,所以分式上下只能乘若干次
2
2
2 得到这样的结果:假设分子是上述无法转化的情况。
7
3
?
2
?
2
?
2
?
2
?
.
.
.
.
.
.
2
?
2
?
2
?
2
?
.
.
.
.
.
.
=
1
?
\dfrac{7}{3}·\dfrac{2·2·2·2·......}{2·2·2·2·......}=1 ?
37??2?2?2?2?......2?2?2?2?......?=1?
说实话显而易见,分子乘
2
2
2没有意义, 因为它离
1
1
1越来越远, 如果最后比值通过分母乘
2
2
2一直到
1
1
1的话,那么一开始分子就应该是
k
?
2
k*2
k?2, 与假设矛盾。
所以这道题只需要建小顶堆,然后判断 是否可以整除分母,是否可以由分母乘2若干次得到这个分子即可。
之前说了,如果过程中有一对数无法转化就永远不可能转化,直接输出
?
1
-1
?1.
#include <iostream>
#include <cstring>
#include <algorithm>
#include<queue>
using namespace std;
typedef long long LL;
const int N = 2e5+10;
LL a[N];
int main()
{
LL n;
cin>>n;
priority_queue<LL, vector<LL>, greater<LL>> heap;
while (n -- )
{
LL x;
scanf("%lld",&x);
heap.push(x);
}
LL cnt=0;
while(heap.size()>1)
{
LL a = heap.top(); heap.pop();
LL b = heap.top(); heap.pop();
if(a==b)
{
heap.push(a+b);
}
else
{
LL flag=0,y=0;
if(b%a==0)//条件一:整除堆顶
{
for(LL i=a;i<=b;i*=2)
{
if(i==b) {flag=1;break;}
y++;
}
}
else//有一对不能整除直接走!
{
printf("-1\n");
return 0;
}
if(flag==1)//条件二:次堆顶可以由堆顶转化
{
cnt=cnt+y;
heap.push((LL)2*b);
}
else //有一对不能由乘2转化也直接走
{
printf("-1\n");
return 0;
}
}
}
cout<<cnt<<endl;
}
H - Theater Square
题意:给一个矩阵和喷泉矩阵的坐标。砖块是用来铺除了喷泉以外的区域,只可以1X2横向铺,如果这一行的宽度不允许或者喷泉的位置不允许我们横着铺满的话,可以选择打碎这个砖块,变成两个1X1的小砖块,但是我们希望打碎这个操作较少,对于题目给定的矩阵,求打碎砖块的最小值。
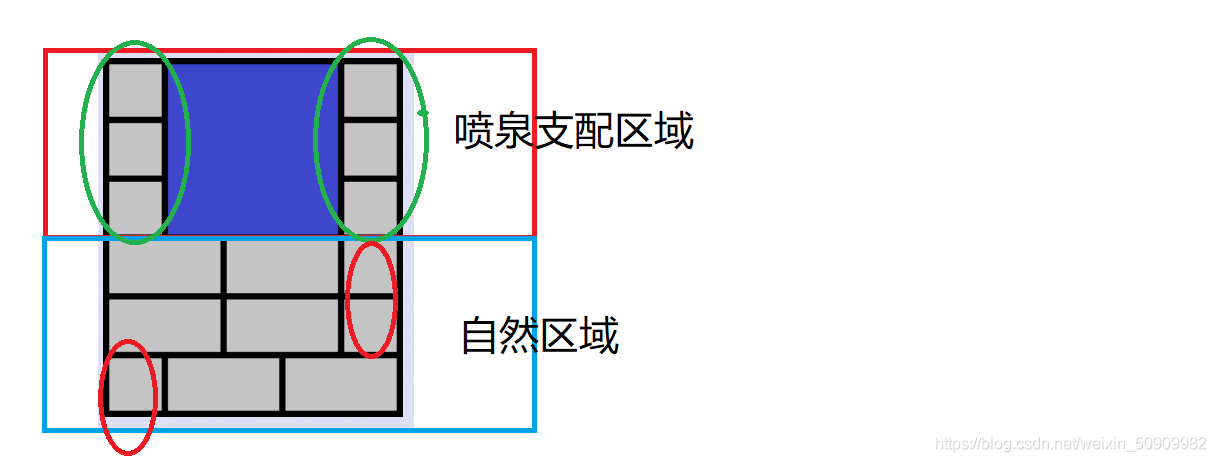
思路:这道题做的时候有点不自信,也WA了几发,看了看别人的题解写的确实比我简洁,但是思路和我基本一致,那我就不改了。
简单来说就是划分喷泉支配和自然区域两个部分,自然区域直接把棋盘宽度%2。支配区域也是看左右宽度+分类讨论,具体看代码注释,比较简单。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e5+10;
LL a[N];
LL vis[N];
int main()
{
LL n,m,x1,y1,x2,y2;
cin>>n>>m;
cin>>x1>>y1>>x2>>y2;
LL left; left=(y1-1)%2;//喷泉支配区域的左边宽度
LL right; right=(m-y2)%2;//喷泉支配区域的右边宽度
LL bom=m%2;//先判断出去喷泉之外的取余的打碎情况
LL len=n-x2+x1-1;//除去喷泉之外的宽度
LL ans,res=0;
ans=len*bom;//除去喷泉之外范围内打碎的 1X1 小格个数。
if(left&&right)//对喷泉支配范围内左右讨论即可得到打碎的结果。
{
res+=(x2-x1+1);
if(ans%2==0) res+=ans/2;
else res+=ans/2+1;
}
else if(!left&&!right)//左右都不需要打碎,只考虑自然区域
{
if(ans%2==0) res+=ans/2;
else res+=ans/2+1;
}
else//左右有一边需要打碎
{
LL sum=ans+x2-x1+1;
if(sum%2==0)
res=res+(ans+x2-x1+1)/2;
else res=res+(ans+x2-x1+1)/2+1;
}
cout<<res<<endl;
}
J - Buying a TV Set
题意:水题
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 3010;
LL a[N];
int main()
{
int n;
//cin>>n;
for(int i=1;i<=4;i++) cin>>a[i];
LL x=__gcd(a[3],a[4]);
a[3]=a[3]/x;
a[4]=a[4]/x;
LL y=min(a[1]/a[3],a[2]/a[4]);
cout<<y<<endl;
}
I - Heist
题意:签到
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 3010;
int a[N];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n);
cout<<a[n]-a[1]-n+1<<endl;
}
A - Coffee Break
题意:
题意:先给出三个数,n,m,d,下面是n个数表示想在
a
i
a_i
ai?时刻快乐(休息),每天工作m分钟,每次快乐的间隔不能小于
d
d
d,问:最少要经过多少天才能把想快乐的时刻都快乐完.(
a
i
a_i
ai?不相同)
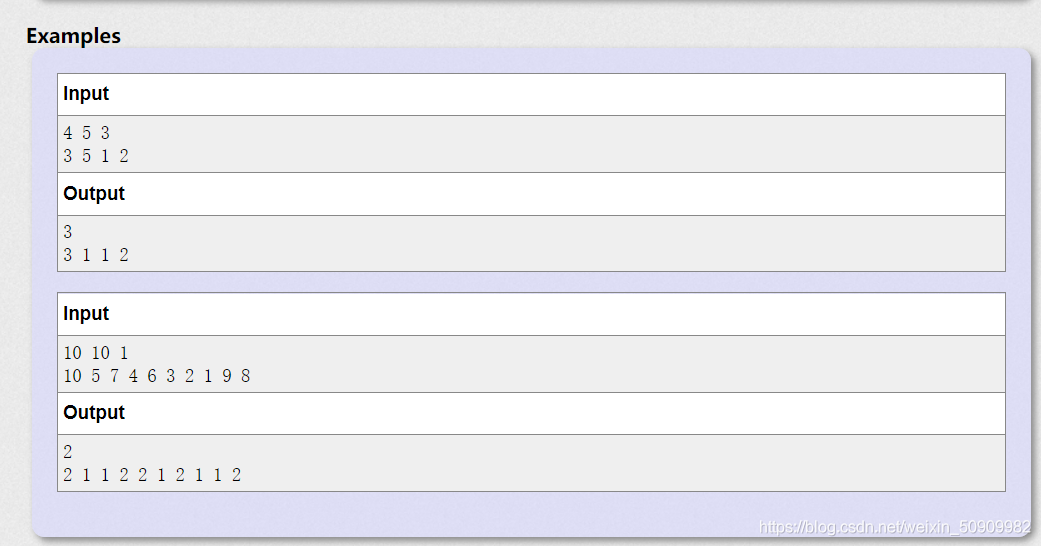
思路:这道题就相当于给循环赋值的过程,先考虑暴力,从小到大赋值天数,直到数组全部完成赋值为止,显然这种做法是超时的,但是超时代码一定对答案有贡献。
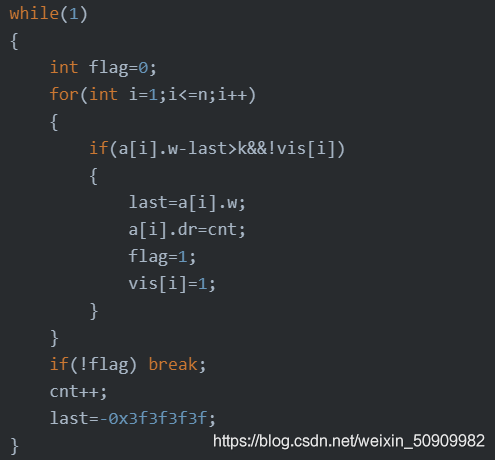
现在问题就是如何优化时间复杂度。当天数很大而距离很小的时候上述代码显然是
O
(
n
2
)
O(n^2)
O(n2)的,我们考虑有没有一种策略可以
O
(
n
)
O(n)
O(n)枚举,或者是找符合距离的条件元素时以更快的算法。考场上我想到的是二分,天数还是得枚举,然后二分出每一个元素符合条件的距离,以
O
(
n
?
l
o
g
n
)
O(n·log_n)
O(n?logn?)来实现算法,但我不知道如何去重,毕竟用过的元素要被去掉,set二分也不会用,想想也挺麻烦了就放弃。
不过这道题既然可以二分那么就存在二分性,这个二分性显然是单调性,既然存在单调性做法就会很多。我们可以用优先队列存当前最小的休息时刻,
a
i
a_i
ai? ,我们还是从小到大枚举休息时间,如果当前休息时间为
a
k
a_k
ak? ,使得
a
k
?
a
i
<
d
a_k-a_i <d
ak??ai?<d , 因为
a
i
a_i
ai?是最小休息时刻,堆里的元素都比
a
i
a_i
ai? 要大,
a
k
a_k
ak?连与
a
i
a_i
ai?都无法同天休息,显然
a
k
a_k
ak? 不可能与之前堆的元素在同一天完成休息,所以
a
k
a_k
ak?只能新开一天存下来,也恰恰因为从小到大枚举,新开的
a
k
a_k
ak?对于新的一天来说总是最小的时刻,符合题意。如果
a
k
?
a
i
>
d
a_k-a_i >d
ak??ai?>d,那么我们可以通过
m
a
p
map
map 把
a
i
a_i
ai? 的天数传递到
a
k
a_k
ak?,然后把
a
i
a_i
ai?从堆中删掉,让堆自然的更新最小值重复过程。
两次
s
o
r
t
sort
sort 满足题意的输出顺序要求。
#include <iostream>
#include <cstring>
#include <algorithm>
#include<queue>
#include <map>
using namespace std;
const int N = 2e5 + 10;
int n,m,k;
typedef long long LL;
struct coffee
{
LL w;
LL id;
}a[N];
int vis[N];
int cnt=1;//喝的天数
map<LL,LL> mp;
bool cmp1(coffee a,coffee b){ return a.w<b.w;}
bool cmp2(coffee a,coffee b){ return a.id<b.id;}
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++) {scanf("%lld",&a[i].w);a[i].id=i;}
sort(a+1,a+1+n,cmp1);
priority_queue<LL,vector<LL>,greater<LL>> q;
q.push(a[1].w);
mp[a[1].w]=1;
for(int i=2;i<=n;i++)
{
auto t=q.top();
if(a[i].w-t> k)
{
q.pop();
mp[a[i].w]=mp[t];
}
else
{
mp[a[i].w]=++cnt;
}
q.push(a[i].w);
}
sort(a+1,a+1+n,cmp2);
cout<<cnt<<endl;
for(int i=1;i<=n;i++) printf("%lld ",mp[a[i].w]);
}