[数据结构与算法]剑指offer 41-50

41.数据流中的中位数(好难系列）

这个题的神仙解法很有意思，也把堆的使用玩到极致，简直是叹为观止!!!

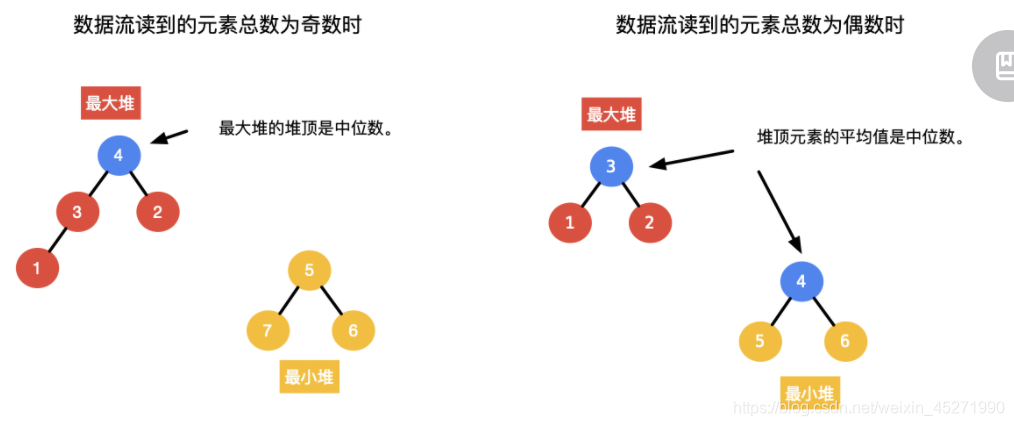
前有序数组由于只关注最大值，可以 动态地 放置在一个最大堆中；

后有序数组由于只关注最小值，可以 动态地 放置在一个最小堆中。

构建两个堆的做法其实本质上也是为了一个有序的，但没有必要让数据整体有序，我们对除了中位数以外的其它位置的元素并不关心，而堆就可以做到取最值的操作。

如何实现来构造这样的两个堆？

那么如何获取中值呢？

class MedianFinder {

    /** initialize your data structure here. */
    PriorityQueue <Integer> queue1 = null; //小根堆
    PriorityQueue <Integer> queue2 = null; //大根堆


    public MedianFinder() {
        queue1 = new PriorityQueue<>();
        queue2 = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return  o2-o1;
            }
        });
    }


    public void addNum(int num) {
        if(queue1.size()  == queue2.size()){ //取当前的和大根堆的堆顶里面最大的放入小根堆
            queue2.add(num);
            queue1.add(queue2.poll());
        }else { //取当前的和小根堆里最小的放入大根堆
            queue1.add(num);
            queue2.add(queue1.poll());
        }

     }

    public double findMedian() {
        if(queue1.size() == queue2.size()){
            return (queue1.peek()+queue2.peek()) /2.0;
        }
        return queue1.peek();
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

42.连续子数组的最大和（※※）

经典中的经典！！！
使用动态规划
dp[i] 代表以元素 nums[i] 为结尾的连续子数组最大和。
状态转移方程
dp[i] = Math.max(dp[i-1]+num[i] , nums[i]);
有可能之前的数字出现了负数的情况，加上这个数字，还不如从当前的数字开始进行连续的和大。
由于之和前一个do[i-1] 有关，所以直接优化成一个一维变量来做。

class Solution {
    public int maxSubArray(int[] nums) {
        int res = 0; //表示的是到arr[i] 结尾的最长连续子数组的和
        int max = 0;
        for (int i = 0 ;i < nums.length;i++){
            res = Math.max(res+nums[i],nums[i]);
            max  = Math.max(res,max);
        }
        return max;
    }
}

43.1~n 整数中1出现的次数（好难系列）

这个题本来以为是个hard ，稍微放一放，结果发现面经里面有抽到这个题的。
难得是这个题得规律，这种题是在找不出规律，看别人怎么写的规律，然后自己记住，只能这样了。
难得是思路，不是代码。
按照去求每一位可能出现的1的个数来计算
小于等于 n 的所有数字中，个位上出现 1 的次数 + 十位出现 1 的次数 +…最后得到的就是总的出现次数。
规律就是

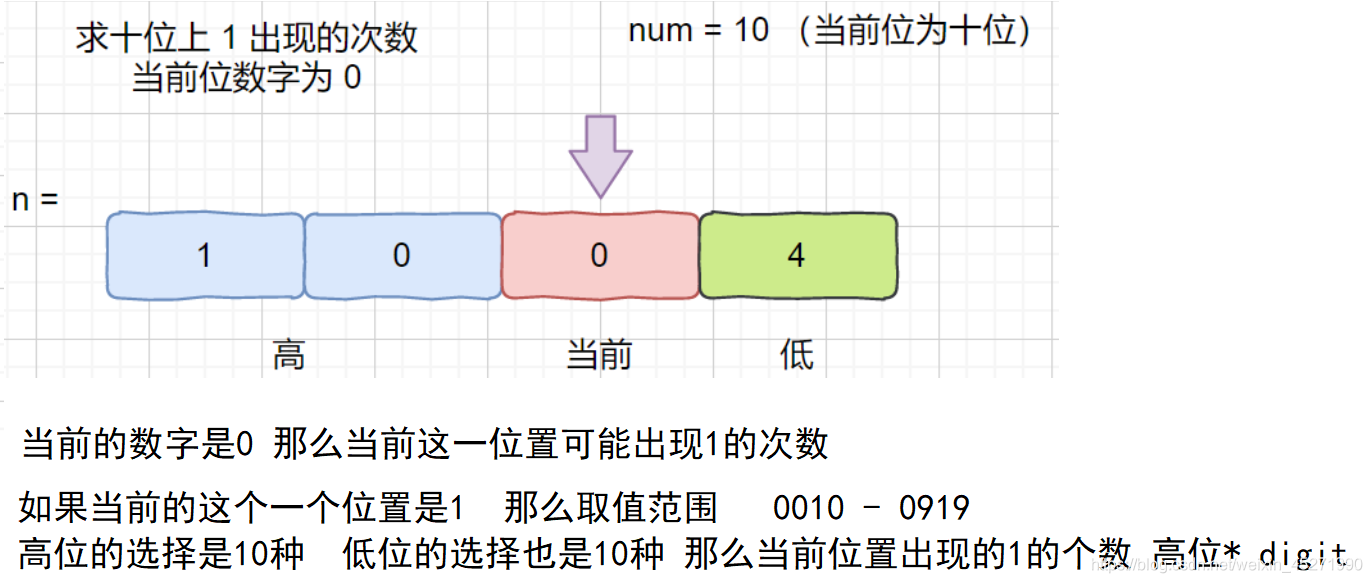
如果当前位是0 那么 可以得到的1的个数 高位*digit
如果当前位是1 那么可以得到的1 的个数 高位 *digit + 低位
如果当前的位不是上面的两种情况 可以得到的1的个数 （高位+1） * digit

看到的比较好理解的一种做法是想象成一个密码箱子的滚轮

 /**
     * 变量需要有
     * high 记录高位
     * cur 记录当前位
     * low 记录低位
     * digit 记录乘积因子
     * 判断当前位是否是1
     * 如果是0 那么当前位可能出现1的个数是  = hight* digit
     * 如果是1  那么当前位得1 的个数是 = high*digit + low+1
     * 如果是其他 那么当前位得1 会产生1的个数是（ high+1）*digit
     * @param n
     * @return
     */
class Solution {
    public int countDigitOne(int n) {
        int high = n/10;
        int cur = n%10;
        int low = 0;
        int digit = 1;
        int count = 0;
        while(high != 0 || cur != 0){
            if(cur==0){
                count += high*digit;
            }else if(cur ==1){
                count += high*digit + low+1;
            }else {
                count += (high+1)* digit;
            }
            low += cur*digit;
            cur = high %10;
            high = high/10;
            digit *= 10;
        }
        return  count;
    }
}

这里面注意一下while得控制循环的语句
注意这个while 条件
最后依次循环得时候 high 其实是已经为0了 所以要些cur ！= 0
但是有可能第一次得cur == 0 所以 high ！=0也是一个条件

44. 数字序列中某一位的数字

这是一道找规律的题。规律有点难找。

这里说的是n 的范围 但是数字的范围一定会越界的，所以用long 存储

class Solution {
    public int findNthDigit(int n) {
        int digit = 1;//记录位数
        long start = 1;
        long count = digit*start*9;
        //大概求出这个数字的位数到底第几位 是一位数字还是两位数字
        //通过一位数字的count只有9 个 两位数字的count 有180 这样来确定
        while (n > count){
            n -= count;
            digit += 1;
            start *= 10;
            count = digit*start*9;
        }

        //这里的n 可以确定了是所有digit位数的数字里面的第 n位
        //先确定这个第n位所在的数字
        long num = start + (n-1)/digit;


        //然后在确定是num的第几位 因为是从0 开始的所以要减去1
        n = (n-1) % digit;
        //所以确定是num的第n位
        char ch = Long.toString(num).charAt(n) ;
        return ch-'0';
    }
}

这个题真的把人整大无语了，美女叹气，哎！
事实上一个星期以前我就打开了它，但是每一次看我都看不进去，看不懂，但我今天死磕了一下，磕懂了，也许？

45.把数组排成最小的数（※）

原来的想法是全部拿出来，拼接成一个字符串，转成成字符数组，排序，然后特殊判断第一个是不是0 ，但是是我敷衍了。确实出现了一些问题！

public  static String minNumber1(int[] nums) {
        if(nums == null || nums.length == 0) return "";
        StringBuilder sb = new StringBuilder();
        for(int num : nums){
            sb.append(num);
        }
        String str = sb.toString();
        char[] arr = str.toCharArray();
        Arrays.sort(arr);
        if(arr.length == 1) return new String(arr);

        if(arr[0] != '0') return new String(arr);
        char temp = arr[0];
        arr[0] = arr[1];
        arr[1] = temp;
        return new String(arr);
    }

问题的原因： 原来的数组是不可以拆开的 就是不可以交换顺序的

如果是数组是 0，1 那么 最后的结果也要是01 不可以是10

那么正确的解题思路是一种另类的排序。，但是比较大小的时候，有一种特殊的规律，这里的证明就不再过多的研究了。

• 如果x + y > y+ x 说明 x “大于” y 这里的大于 说明 x 应该放在 y的后面
• 如果x + y < y +x 说明 x “小于” y

那么使用任何一种排序即可。
这里使用插排的思想，主要是写起来比较方便。

x 代表遍历的有序区间 y 代表当前需要排序的数字
如果x + y > y+ x 说明 x “大于” y 那么就需要让x 往后挪动一个位置
如果x + y < y +x 跳出循环 说明 x “小于” y 当前遍历的到j 的下一个位置是y 应该在的位置。
题解
具体的证明参考题解以及例子的示例即可。

class Solution {
    public String minNumber(int[] nums) {
        //排序的比较次数
        // 有序区间 [0-i)
        //无序区间 [i,arr.length)
        //每次拿出无序区间的第一个数字 然后遍历有序区间插入
        //找出循环次数和区间的关系
        for(int i = 1;i < nums.length;i++){
            //遍历
            int key = nums[i];
            int j = i - 1;
            for(; j  >=0 ;j--){
                //这里换一下比的规则
                StringBuilder sb = new StringBuilder();
                sb.append(nums[j]).append(key);
                StringBuilder sb2 = new StringBuilder();
                sb2.append(key).append(nums[j]);
                if(sb.toString().compareTo(sb2.toString()) > 0){
                    nums[j+1] = nums[j];
                }else {
                    break;
                }
            }
            nums[j+1] = key;
        }

        StringBuilder sb = new StringBuilder();
        for(int num : nums){
            sb.append(num);
        }
        return sb.toString();
    }
}

46.把数字翻译成字符串 （※）

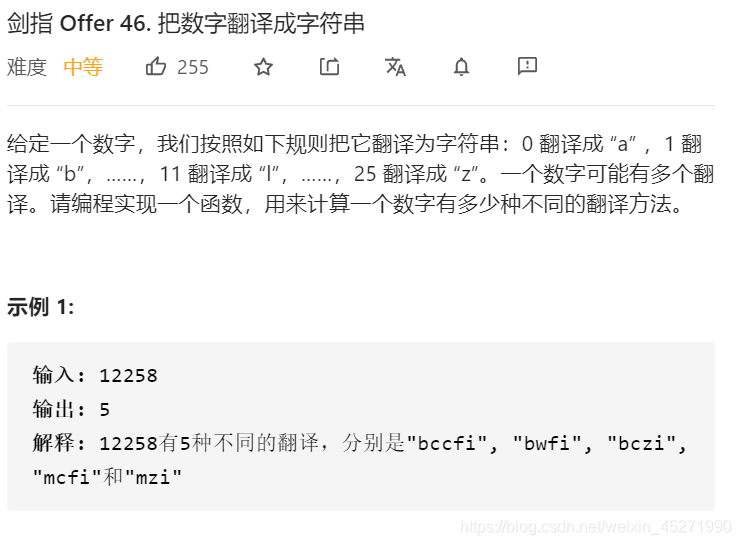
思路一 ： 动态规划
dp[i] 表示的是到第i个字母可以有多少种翻译结果,同时多开辟一个空间防止越界。
dp[i] 的结果应该是 前一个字符可以形成的结果 dp[i-1]
同时判断 i- 1 和i是否可以翻译 如果可以再加上 前两个字符形成的结果dp[i-2]

注意比如 前一个字符是2种结果 到当前的i 还是2种结果，不是+1嗷！

class Solution {
    public int translateNum(int num) {
        String str = Integer.toString(num);
        int length = str.length();
        int[] dp = new int[length+1];//表示的是到第i个字母一共有多少种翻译方法
        dp[0] =1;
        for(int i = 1; i <= length;i++){
            char ch = str.charAt(i-1);
            if(ch >= '0' && ch <= '9'){
                dp[i] += dp[i-1];
            }
            if(i>1){
                String temp = str.substring(i-2,i);
                int number = Integer.parseInt(temp);
                if(number >= 10 && number <= 25) dp[i] += dp[i-2];
            }
        }
        return dp[length];
    }
}

思路二：滚动数组优化

其实在上面判断第i 是不是0-9 是没有必要的，因为本身参数就是整数，所以说不用这做！
也就是说只用判断当前i-1 和 i是否符合要求，如果符合那就 说明这两位可以翻译，那么dp[i] =dp[i-1]+dp[i-2]
如果不符合 那么就是 dp[i] = dp[i-1]
显然发现只和前两个有关，那么使用在原来的坐标上优化数组 %2 或者 &1 即可

class Solution {
    public int translateNum(int num) {
        String s = String.valueOf(num);
        int[] dp = new int[2];
        dp[0] = 1;
        for(int i = 1; i < s.length(); i ++){
            String temp ;
            if(i == 1){
                temp = s.substring(0, i+1);
            }else {
                temp = s.substring(i-1, i+1);
            }
            if(temp.compareTo("10") >= 0 && temp.compareTo("25") <= 0){
                if(i== 1) dp[1] = dp[i-1 &1] + 1;
                else dp[i%2] = dp[i-1&1]  + dp[i-2&1];
            }else{
                dp[i % 2] = dp[i - 1 & 1];
            }
        }
        return dp[s.length()-1 &1];
    }
}

47.礼物的最大价值

思路：动态规划

class Solution {
    public int maxValue(int[][] grid) {
       int m = grid.length;
       int n = grid[0].length;
       int dp[][] = new int[m+1][n+1];

       for(int i = 1;i <= m;i++){
           for(int j =1; j<= n;j++){
               dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
           }
       }
       return dp[m][n];
    }
}

发现是不可以使用二维优化的，但是一个比较厉害的做法使用了原理更改数组的做法。
也就是滑动数组的做法
也就是原地更改数组的方式来做！

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for(int i = 0;i < m;i++){
            for(int j =0; j< n;j++){
                //考虑到越界的问题
                //第一行
                if(i == 0) {
                    if(j >= 1)grid[0][j] = grid[0][j - 1]+grid[i][j];
                    else continue;;
                }else if(j == 0 ) {
                    grid[i][0] = grid[i - 1][0]+grid[i][j];  //第一列
                } else grid[i][j] =  Math.max(grid[i-1][j],grid[i][j-1])+grid[i][j];
            }
        }
        return grid[m-1][n-1];
    }
}

48.最长不含重复字符的子字符串（※※）

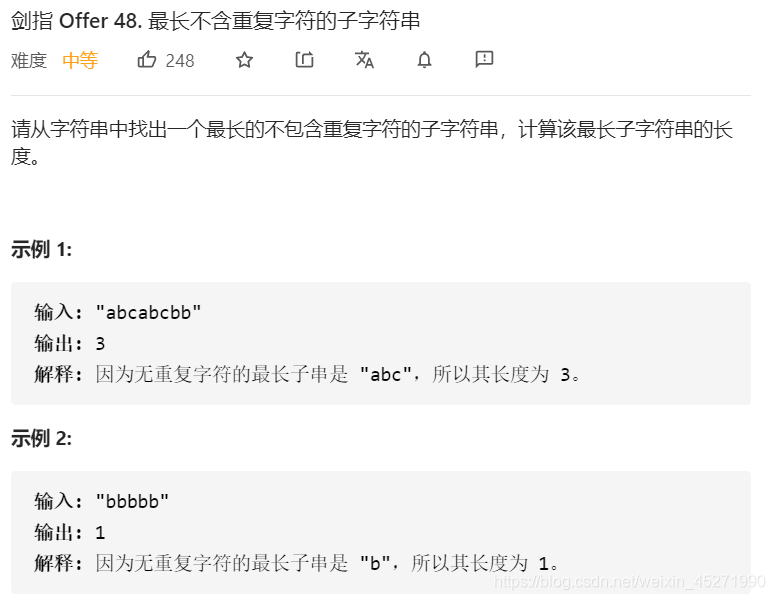
使用双指针/滑动窗口
用一个set来记录之前遍历过的字符，
如果set里面不存在，就一直往里面加入，同时通过set.size来更新最大值。
如果遇到相等的那么就一直从set里面弹出，直到不相等之后继续统计。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s == null || s.length() == 0) return 0;
        if(s.length() == 1) return 1;
        HashSet<Character> set = new HashSet<>();
        char[] arr = s.toCharArray();
        //枚举每一个作为计算的起点
        int left = 0;
        set.add(arr[left]);
        int right = 1;
        int max = 1;
        while(right < arr.length){
            if(!set.contains(arr[right])){ //如果没有就一直添加 同时记录当前的数量
                set.add(arr[right]);
                right++;
                max = Math.max(max,set.size());
            }else{
                set.remove(arr[left]); //如果有就不断的从set里面删
                left++;
            }
        }
        return max;
    }
}

49.丑数（好难系列）

这个题需要找到数字之间的规律，还是比较难懂的！

根据题意，可以提炼出来一个规律，就是每一个丑数都是由前面的丑数乘以 2 3 5得来的，也就是这样可以得到所有的丑数，可是题目中还有一个要求是丑数必须是按照从小到大排列的，这样依次由每一个丑数乘以 2 3 5得到的数字不一定是有序的

解决的办法
设置3个索引a, b, c，分别记录前几个数已经被乘2， 乘3， 乘5了
比如a表示前(a-1)个数都已经乘过一次2了，下次应该乘2的是第a个数；
b表示前(b-1)个数都已经乘过一次3了，下次应该乘3的是第b个数；
c表示前(c-1)个数都已经乘过一次5了，下次应该乘5的是第c个数；

对于某个状态下的丑数序列，我们知道此时第a个数还没有乘2(有没有乘3或者乘5不知道）， 第b个数还没有乘3(有没有乘2或者乘5不知道），第c个数还没有乘5(有没有乘2或者乘3不知道), 下一个丑数一定是从第a丑数乘2， 第b个数乘3， 第c个数乘5中获得，他们三者最小的那个就是下个丑数。

我们可以比较一下这个新的丑数等于究竟是等于第a个丑数乘2, 还是第b个数乘3， 还是第c个数乘5， 通过比较我们肯定可以知道这个新的丑数到底是哪个数通过乘哪个数得到的
假设这个新的丑数是通过第a个数乘2得到的，下次应该乘2的是第 （a+1） 个数, 所以a++；
同理b c。但是有一个问题就是，如果第a个数乘2后等于第b个数乘3，或者等于第c个数乘5， 说明这个新的丑数是有两种或者三种方式可以得到，这时应该给得到这个新丑数的组合对应的索引都加一，比如新丑数是第a个数乘2后和第b个数乘3得到的，那么 a 和 b都应该加一， 因为此时第a个数已经通过乘2得到了一个新的丑数，第b个数已经通过乘3得到了一个新的丑数, 只不过这两个数相等而已。

class Solution {
    public int nthUglyNumber(int n) {
        int dp[] = new int[n];//用来存储丑数序列

        //分别表示的第a个需要乘以2   a-1 之前的数字都已经乘过2了
        //第b个数需要乘以3
        //第c个数需要乘以4
        int a = 0;
        int b = 0;
        int c = 0;
        dp[0] = 1;
        for(int i= 1;i < n;i++){
            int n2 = dp[a]*2;
            int n3 = dp[b]*3;
            int n5 = dp[c]*5;
            dp[i] = Math.min(Math.min(n2,n3),n5);
            if(dp[i] == n2) a++;
            if(dp[i] == n3) b++;
            if(dp[i] == n5) c++;
        }
        return dp[n-1];
    }
}

50.第一个只出现一次的字符

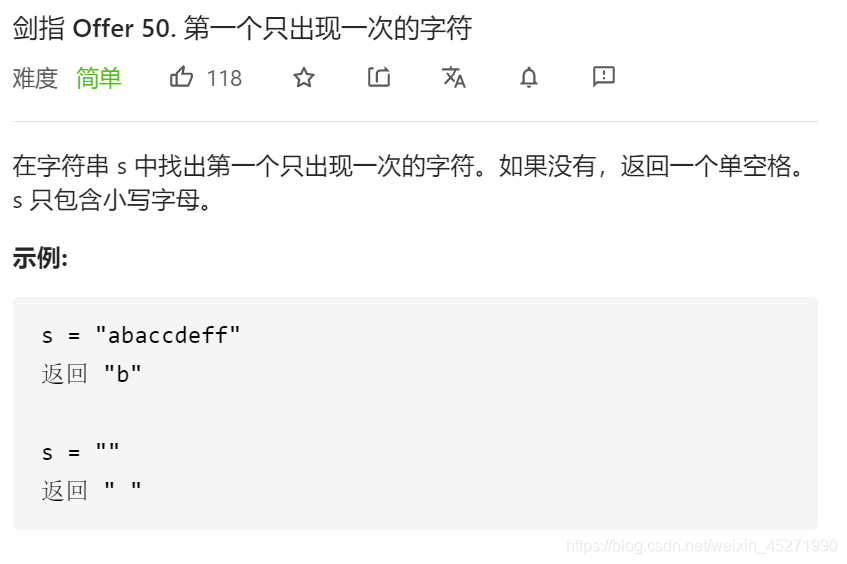
有序哈希表即可！

class Solution {
    public char firstUniqChar(String s) {
        HashMap <Character,Integer> map = new LinkedHashMap<>();
        char[] arr = s.toCharArray();
        for(char ch :arr){
            map.put(ch,map.getOrDefault(ch,0)+1);
        }
        for(Map.Entry<Character,Integer> mapping : map.entrySet()){
            if(mapping.getValue() == 1) return mapping.getKey();
        }

        return ' ';
    }
}

上周定好的计划被一些事情给打乱，导致这周又得重新弄起来，新的东西也开始不了，希望这周效率高点吧！！
真的发现，好运和努力是有关系的