树
树,森林和二叉树的转换
树转换为二叉树
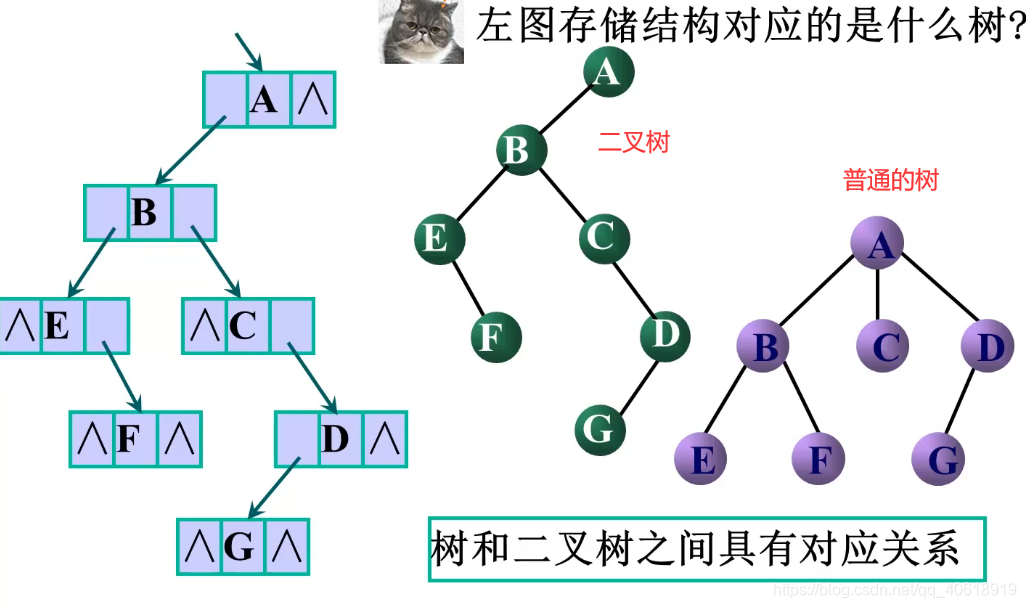
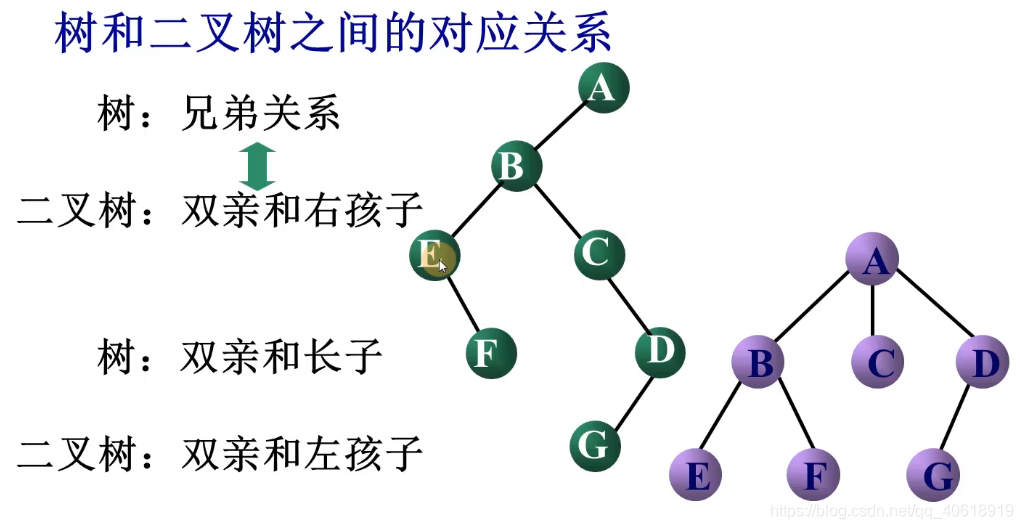
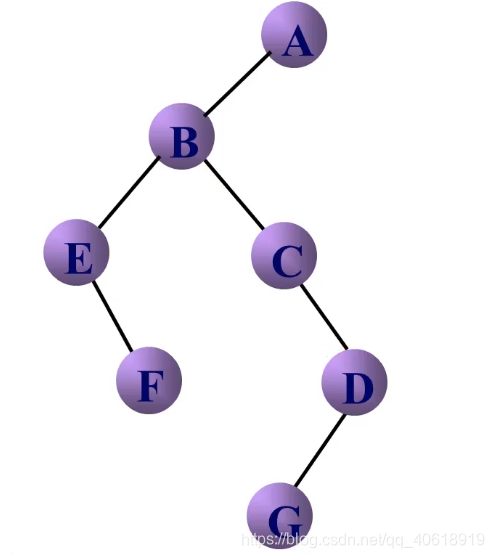
如何将树转换成二叉树:
- 加线:树中所有相邻兄弟之间加一条线
- 去线:对树中的每一个结点,只保留它与第一个孩子结点之间的连线,删去它与其他孩子结点之间的连线
- 层次调整:以根结点为轴心,将树顺时针转动一定的角度,使之层次分明
- 兄弟加线
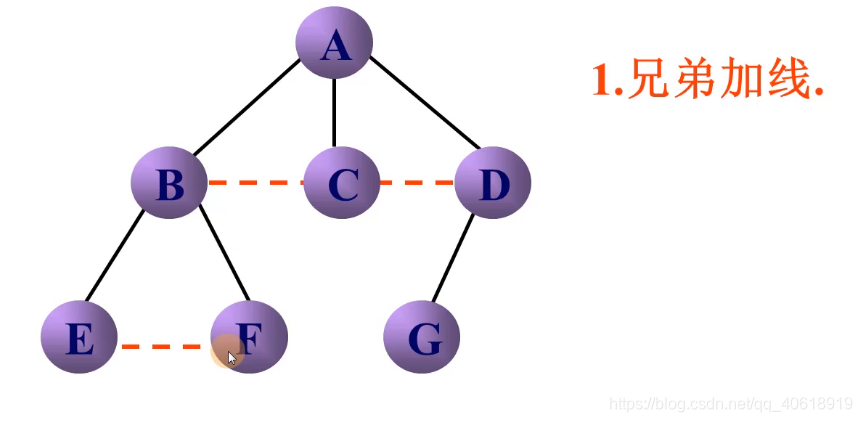
- 保留双亲与第一个孩子连线,删去去其他孩子的连线
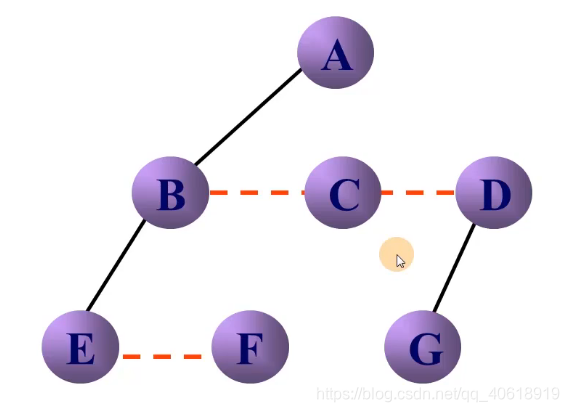
- 顺时针转动,使之层次分明
-
树的前序遍历等价于二叉树的前序遍历
-
树的后序遍历等价于二叉树的中序遍历
森林转换为二叉树
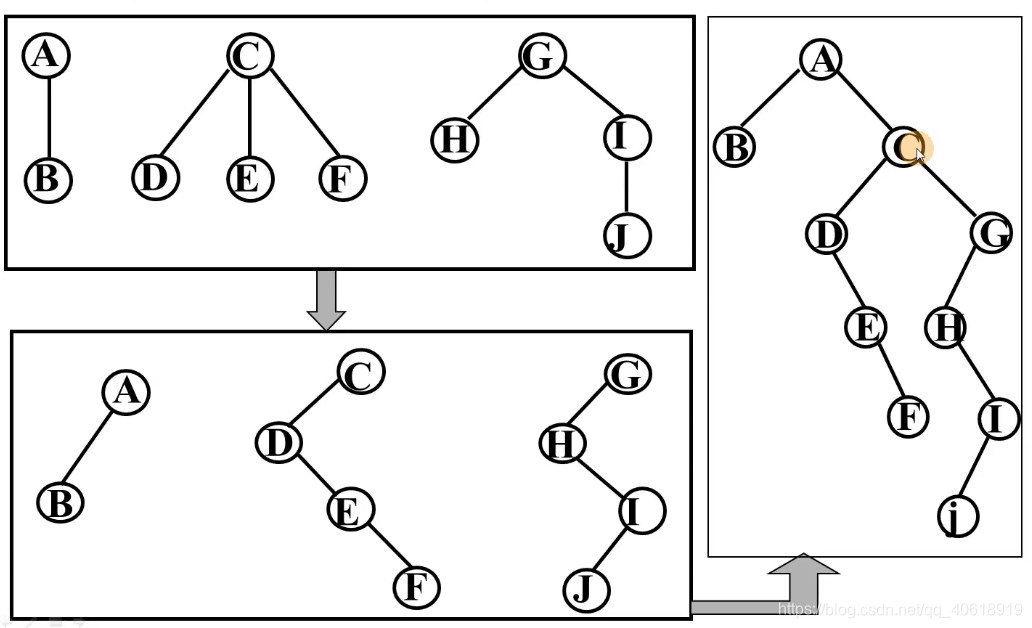
- 将森林中的每棵树转换成二叉树;
- 从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子,当所有二叉树连起来后,此时所得到的二叉树就是由森林转换得到的二叉树。
二叉树转换为树或者森林
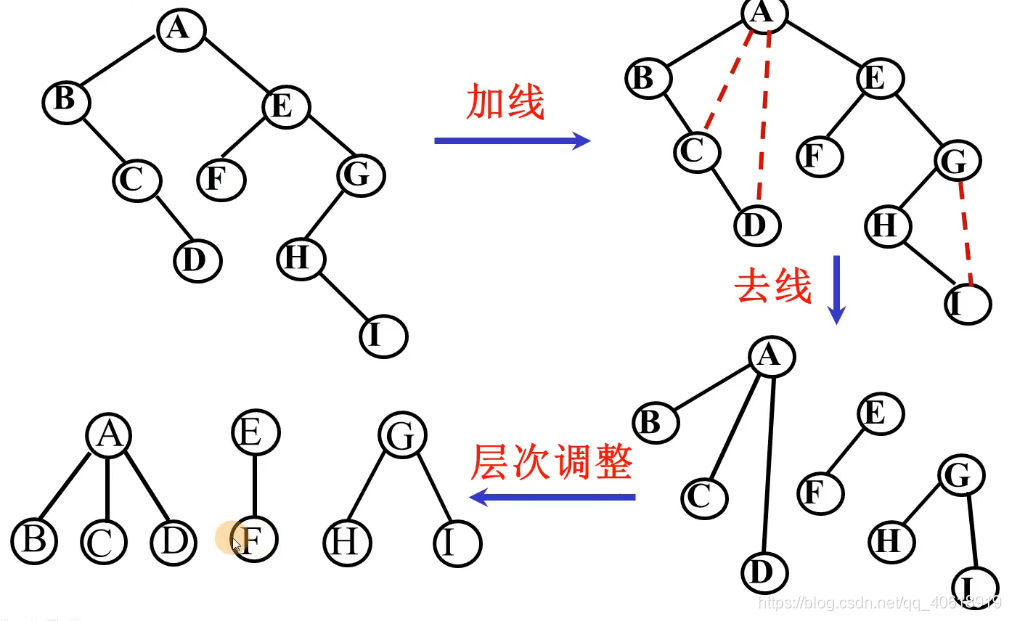
- 加线:若某结点 x 是其双亲 y 的左孩子,则把结点x的右孩子、右孩子的右孩子、… 都与结点 y 用线连起来;
- 去线:删去原二叉树中所有的双亲结点与右孩子结点的连线;
- 层次调整:整理由(1)、(2)两步所得到的树或森林,使之层次分明。
- 二叉树转换为森林

森林的遍历
森林有两种遍历方法:
- 前序(根)遍历:前序遍历森林即为前序遍历森林中的每一棵树。
- 后序(根)遍历:后序遍历森林即为后序遍历森林中的每一棵树。
二叉树遍历的非递归算法
由于递归程序比较耗时,有时候为了提高效率,需要用一些非递归算法。
前序遍历—非递归算法(也称为先序遍历)
- 二叉树前序遍历的非递归算法的关键:在前序遍历完某结点的整个左子树后,如何找到该结点的右子树的根指针。
解决办法:在访问完该结点后,将该结点的指针保存在栈中,以便以后能通过它找到该结点的右子树。
在前序遍历中,设要遍历二叉树的根指针为 root ,则有两种可能:
- 若 root != NULL
- 若 root = NULL
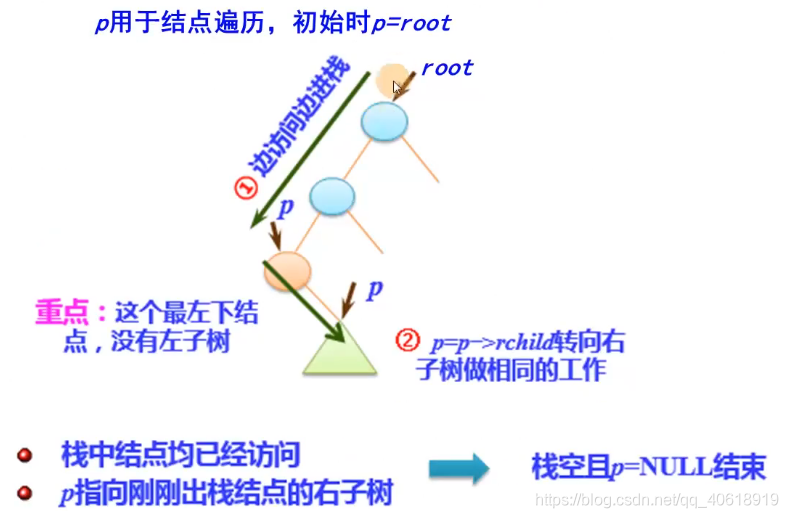
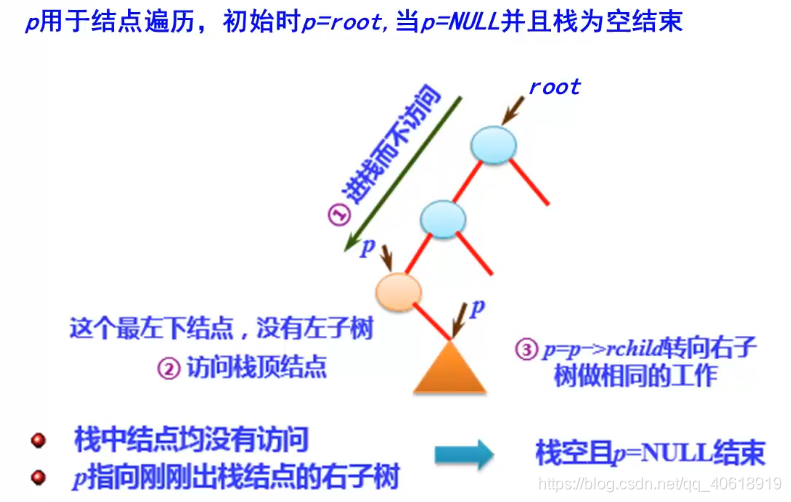
- 上图为一棵树,root 指向根结点,p 用于结点遍历,初始时 p = root
- 前序遍历非递归实现,包括两个大的步骤
- p 从 root 开始,一边访问根结点,一边将这个结点入栈,然后进入左子树,继续访问这个结点,将这个结点进栈,继续访问左子树。从根结点开始,一边访问一边进栈,当最左下角的结点没有左子树时,第一步结束;
- 然后进入第二步,p 指向 p 的右子树,做同样的工作
前序遍历非递归实现
-
开始时,p 指针指向根结点,访问A结点,将它输出,并入栈,

-
p 指针会从A结点转而指向它的左子树B结点,B结点会被访问,并且入栈,

-
然后转向它的左子树 D,D 也会被访问,并且入栈
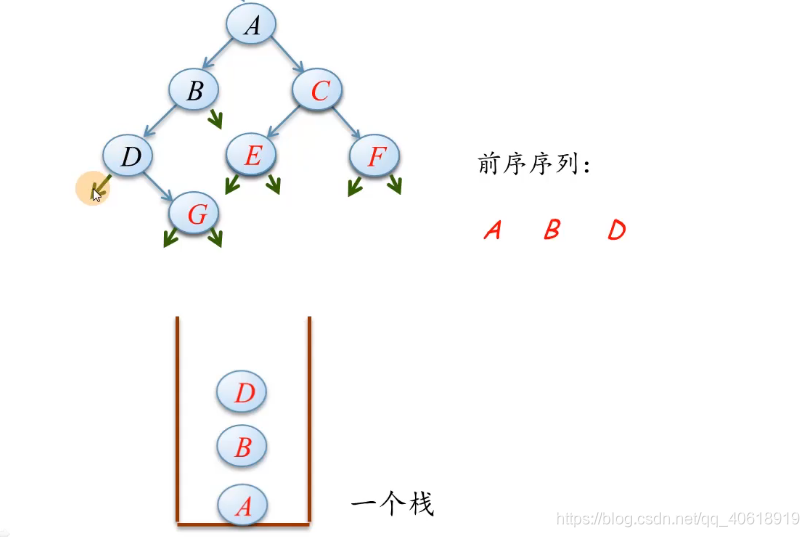
- p 指向 D 的左子树,p 当前为空,此时栈顶的元素需要出栈,并且让 p 回退到栈顶元素所在的位置,此时 D 出栈,p 指向 D 结点,转向进入第二步,遍历右子树,做同样的工作。

- 进入第二步,p 指向 D 的右子树,将 p 所在的结点 G 访问,并且入栈,
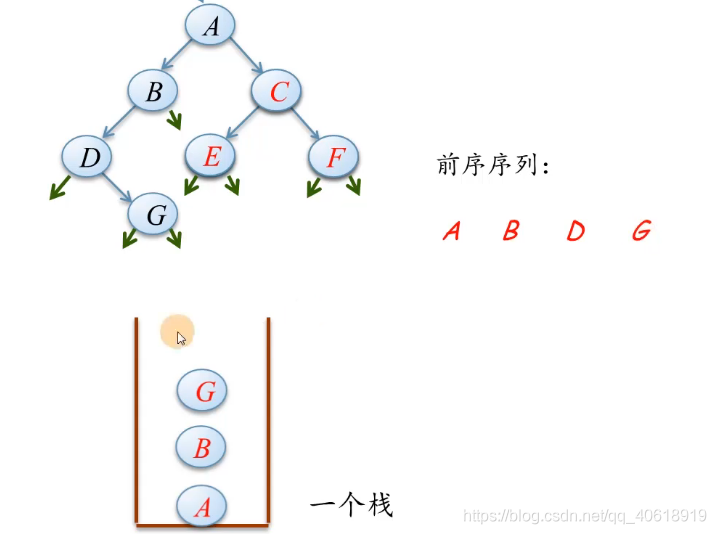
- 接下来重复前面相同的步骤,p 继续访问 G 的左子树,左子树为空,G 需要出栈,p 回退到G,开始指向 G 的右子树,此时 p 为空,需要将栈顶的元素出栈,
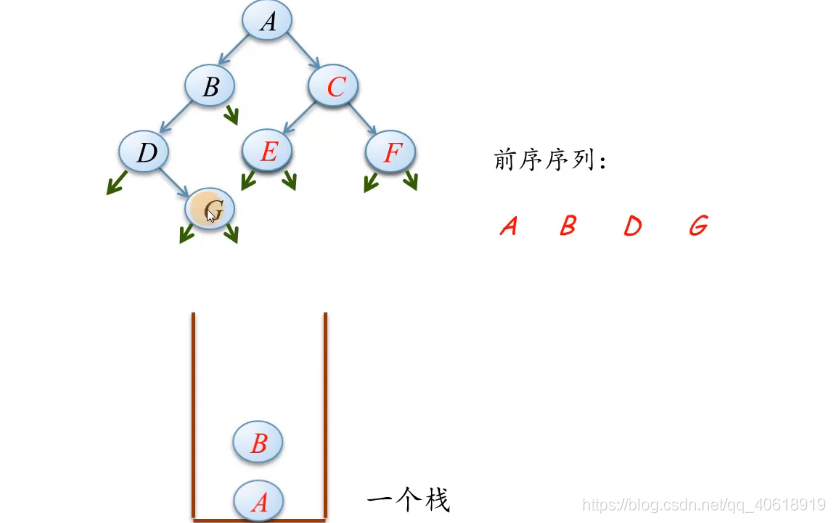
- 此时 B 出栈,让 p 指针指向 B 结点,此时 B 结点的左子树全部访问完毕,接下来转向访问它的右子树,p 指向空指针,右子树为空,此时需要栈顶元素出栈,

- A 元素出栈,p 指针回退到 A 结点,此时 A 结点的左子树全部访问完毕,此时执行第二个步骤,

- p 指向 A 的右子树,访问 C 结点,并且将 C 结点入栈,

- 然后 p 指针指向 C 的左子树,访问 E 结点,并且入栈,接着访问 E 的左子树,发现左子树为空,E 出栈,p 回退到 E,访问 E的右子树,右子树也为空,C 出栈,p 回退到 C,访问 C 的右子树,p 指针访问F,F 入栈,
 .
.
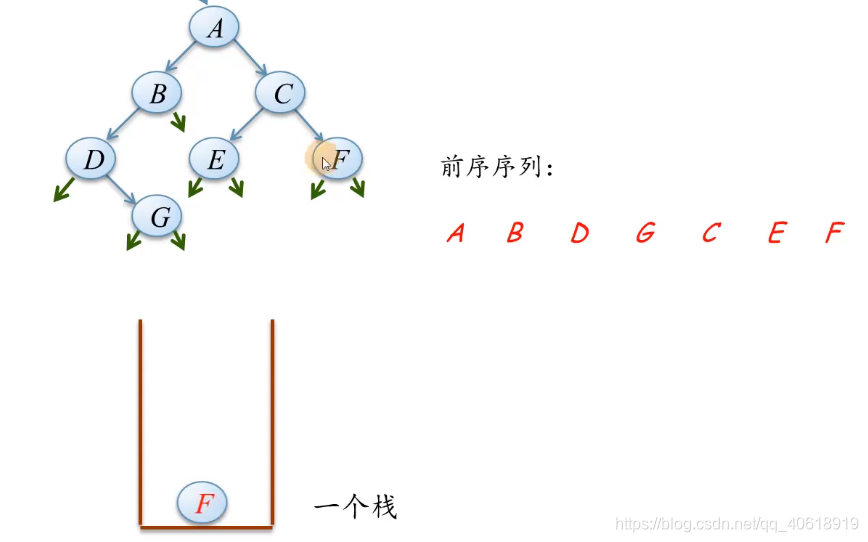
- p 指针访问 F 的左子树,为空,F 出栈,p 回退到 F ,p 访问 F 的右子树,右子树为空,而此时的栈也为空,故前序遍历完毕

伪代码


中序遍历—非递归算法
- 在二叉树的中序遍历中,访问结点的操作发生在该结点的左子树遍历完毕并准备遍历右子树时,所以,在遍历过程中遇到某结点时并不能立即访问它,而是将它压栈,等到它的左子树遍历完毕后,再从栈中弹出并访问之。中序遍历的非递归算法只需将前序遍历的非递归算法中的输出语
句 visit(bt- ->data) 移到 p = s. pop() ; 之后即可。
后序遍历—非递归算法
在后序遍历过程中,结点要入两次栈,出两次栈:
- 第一次出栈:只遍历完左子树,该结点不出栈,利用栈顶结点找到它的右子树,准备遍历它的右子树;
- 第二次出栈:遍历完右子树,将该结点出栈,并访问它。因此,为了区别同一个结点的两次出栈,设置标志flag。

