机器学习学习记录 1.线性回归
单变量线性回归
#调用所需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#读取文件
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])#read_csv用来读取文件
data.head() #只观察前5行数据(只能读取前五行数据)
data.describe() #统计一个datafram的信息,观察一系列数据的范围、大小、波动趋势。
其中**describe()**函数功能返回值如下:
| Population | Profit | |
|---|---|---|
| count | 总数量 | |
| mean | 均值 | |
| std | 标准差 | |
| min | 最小值 | |
| 25% | 四分之一分位数 | |
| 50% | 二分之一分位数 | |
| 75% | 四分之三分位数 | |
| max | 最大值 |
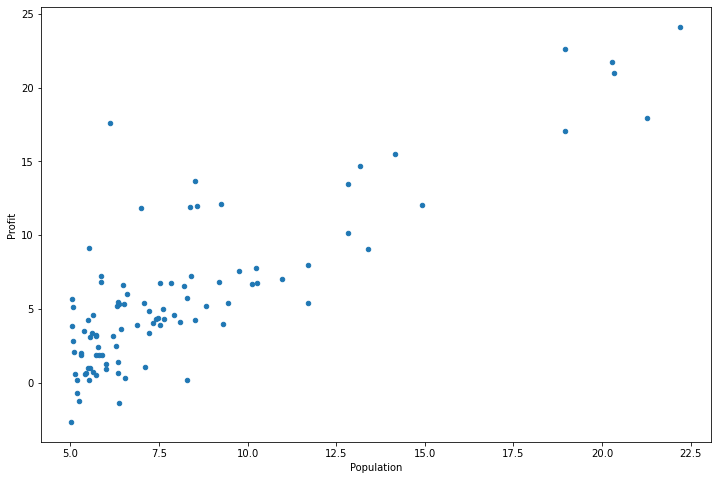
将数据可视化(画图)
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))#画散点图,x和y分别是其横纵坐标标签,figsize是其图像大小
plt.show()#展示画出的图像
代价函数
创建一个以参数
θ
\theta
θ?为特征函数的代价函数
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2
J(θ)=2m1?i=1∑m?(hθ?(x(i))?y(i))2
其中:
h
θ
(
x
)
=
θ
T
X
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
h_\theta(x)=\theta^TX=\theta_0x_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n
hθ?(x)=θTX=θ0?x0?+θ1?x1?+θ2?x2?+...+θn?xn?
创建代价函数
def computeCost(X, y, theta):
## X,y为样本的输入和输出,theta为参数
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
让我们在训练集中添加一列,以便我们可以使用向量化的解决方案来计算代价和梯度。
data.insert(0, 'Ones', 1) #第一列插入列名为Ones的全为1的向量
变量初始化
# set X (training data) and y (target variable)
cols = data.shape[1]#=3读取第二维长度,第一维用shape[0].data:97*3
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列 iloc函数:提取行或者列数据
y = data.iloc[:,cols-1:cols]#y是所有行,最后一列
初始化theta同时将数值转换为矩阵进行计算
X = np.matrix(X.values)#values是把csv文件中的值取出来97*2
y = np.matrix(y.values)#1*2
theta = np.matrix(np.array([0,0]))#theta是1*2矩阵
此时可以计算代价函数(theta初始值为0)
computeCost(X, y, theta)
批量梯度下降
θ j : = θ j ? α ? ? θ J ( θ ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta}J(\theta) θj?:=θj??α?θ??J(θ)
def gradientDescent(X, y, theta, alpha, iters):
# X为特征输入,y为特征输出,theta为参数,alpha为学习率,iters为执行的迭代次数
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:,j])
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost
执行梯度下降算法
alpha = 0.01
iters = 1000
g, cost = gradientDescent(X, y, theta, alpha, iters)
#g是通过计算所得到的theta matrix([[-3.24140214, 1.1272942 ]])
通过拟合后的参数计算计算训练模型的代价函数
computeCost(X, y, g)
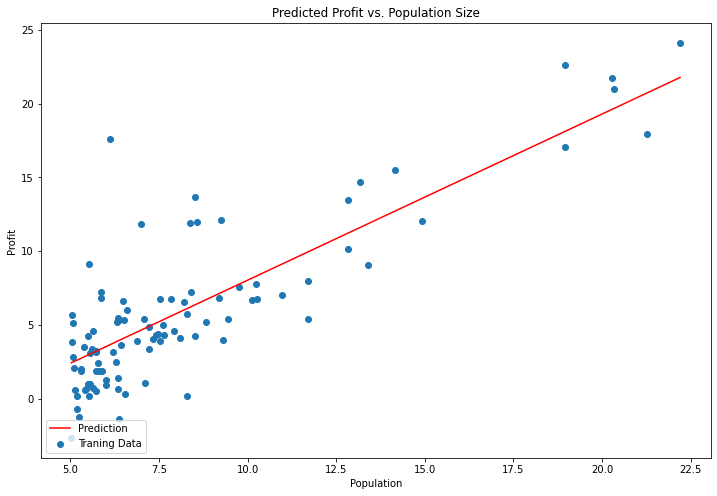
将结果可视化绘制线性模型以及拟合数据(可由此参考Python画图的一般步骤)
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)
fig, ax = plt.subplots(figsize=(12,8))#以子图模式画图,正常用法为plt.subplots(1,2,figsize=()),ax[0]...ax[1]...
ax.plot(x, f, 'r', label='Prediction')#画x,f图
ax.scatter(data.Population, data.Profit, label='Traning Data')#画散点图
ax.legend(loc=3)#图中标签的位置,loc=1,右上角,loc=2,左上角,loc=3,左下角,loc=4,右下角
ax.set_xlabel('Population')#设置x轴标签
ax.set_ylabel('Profit')#设置y轴标签
ax.set_title('Predicted Profit vs. Population Size')#设置题目标签
plt.show()#展示图片
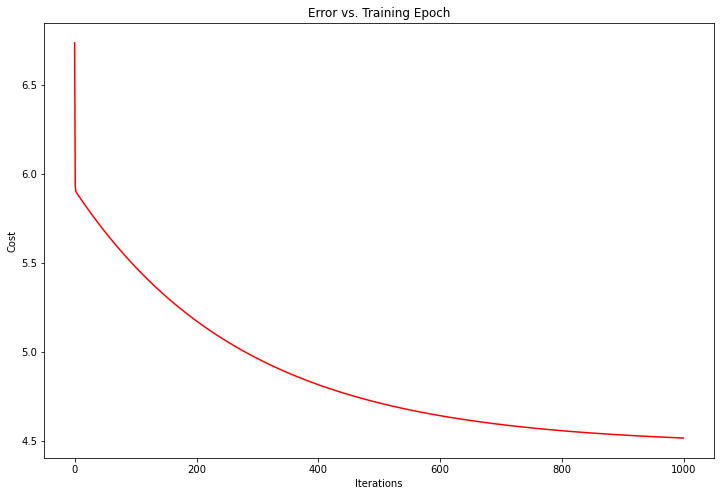
同样也可以绘制迭代次数和代价函数之间的关系
fig, ax = plt.subplots(figsize=(12,8))#具体过程可参考上面代码段
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
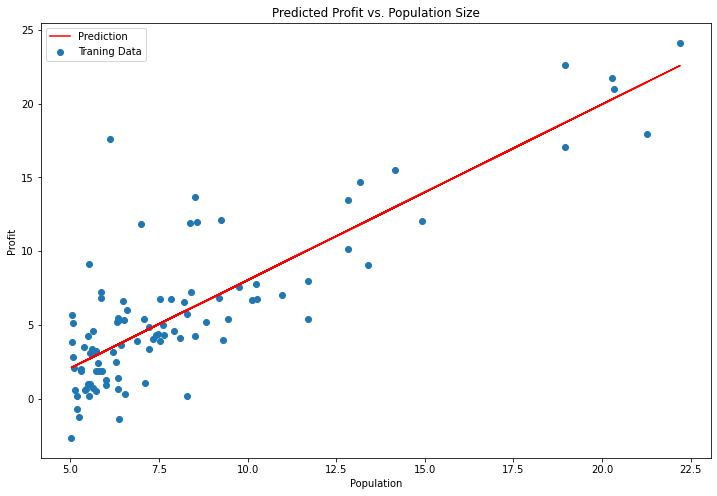
同样也可以使用scikit-learn的线性回归函数来直接应用于第一部分数据,而没有从头开始实现这些算法。
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
#我们来看看scikit-learn model的预测表现
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()#线性回归后的模型预测值
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
多变量线性回归
先读取数据(包括两个变量一个目标)
path = 'ex1data2.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
比之前多出一步:预处理特征归一化
data2 = (data2 - data2.mean()) / data2.std()#特征归一化 std为标准差
接下来重复之前的步骤
# add ones column
data2.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
# get the cost (error) of the model
computeCost(X2, y2, g2)
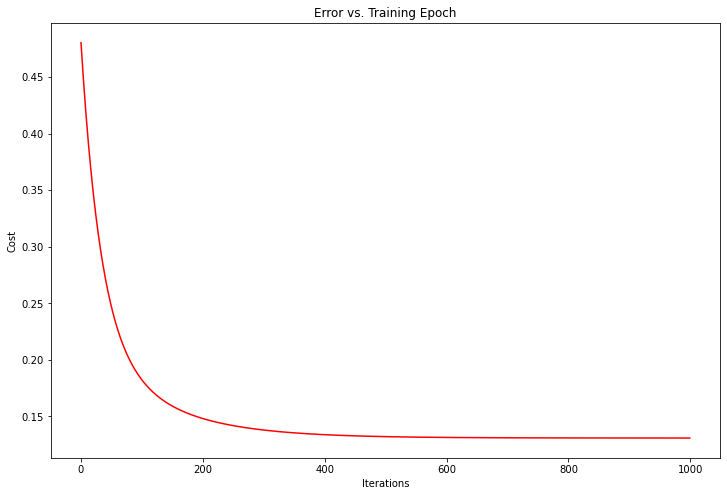
通过图像观察迭代次数与损失函数关系
#过程与之前类似
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
正规方程
通过求解
?
?
θ
j
J
(
θ
j
)
=
0
\frac{\partial}{\partial\theta_j}J(\theta_j)=0
?θj???J(θj?)=0
进而得到代价函数最小参数的过程称为正规方程法。
假设训练集特征矩阵为X(其中包含
x
0
=
1
x_0=1
x0?=1?)同时训练集的结果为向量
y
y
y?,则通过正规方程解得:
θ
=
(
X
T
X
)
?
1
X
T
y
\theta=(X^TX)^{-1}X^Ty
θ=(XTX)?1XTy
上标
T
T
T代表转置矩阵,上标
?
1
-1
?1代表矩阵的逆。设矩阵
A
=
X
T
X
A=X^TX
A=XTX???,则:
(
X
T
X
)
?
1
=
A
?
1
(X^{T}X)^-1=A^{-1}
(XTX)?1=A?1
#正规方程函数
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y#X.T@X等价于X.T.dot(X) np.linalg.inv 求矩阵的逆矩阵 x.T求矩阵的转置矩阵 .dot()矩阵相乘
return theta#theta=np.linalg.inv(x.T.dot(x)).dot(x.T).dot(y)
代入 X X X, y y y,我们可以得到
final_theta2=normalEqn(X, y)#感觉和批量梯度下降的theta的值有点差距
final_theta2#matrix([[-3.89578088],[ 1.19303364]])
#之前梯度下降得到的结果是:matrix([[-3.24140214, 1.1272942 ]])
正规方程与梯度下降比较
梯度下降:需要选择学习率α,需要多次迭代,当特征数量n大时也能较好适用,适用于各种类型的模型
正规方程:不需要选择学习率α,一次计算得出,需要计算 ( X T X ) ? 1 (X^TX)^{-1} (XTX)?1,如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O(n^3) O(n3)?,通常来说当 n < 10000 n<10000 n<10000?时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型。
备注:本次笔记是吴恩达老师的机器学习第一次课后编程题的python版本的笔记记录,欢迎大家学习交流。