Java实现数据结构基本算法——(十一)排序——插入排序(Insertion_Sort)
一、插入排序的定义及分类
插入排序的基本思想:每次将一个待排序的记录按其关键字大小插入到前面已经排好序的子序列中,直到全部记录插入完成。
分类:直接插入排序、折半插入排序、希尔排序。
二、插入排序——直接插入排序
1. 基本思想:
(1)将待排序的记录序列划分位有序区和无序区,初始时有序区为待排记录的第一个元素(只有一个元素arr[0]),无序区包括所有剩余待排的元素(arr[1] 到 arr[arr.length - 1])共arr.length - 1 个元素;
(2)将无序区中的第一个记录插入到有序区的合适位置中,从而使无序区减少一个元素,有序区增加一个元素;
(3)重复执行步骤(2),直到无序区中所有的记录都取完,再也没有剩余元素为止,这样前面的有序区就是经过排序得到的有序序列。
2. 排序过程:
| 元素下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 初始序列 | 【 49 】 | 38 | 65 | 97 | 76 | 13 | 27 |
| 第1躺排序之后 | 【 38 | 49 】 | 65 | 97 | 76 | 13 | 27 |
| 第2躺排序之后 | 【 38 | 49 | 65 】 | 97 | 76 | 13 | 27 |
| 第3躺排序之后 | 【 38 | 49 | 65 | 97 】 | 76 | 13 | 27 |
| 第4躺排序之后 | 【 38 | 49 | 65 | 76 | 97 】 | 13 | 27 |
| 第5躺排序之后 | 【13 | 38 | 49 | 65 | 76 | 97 】 | 27 |
| 第6躺排序之后 | 【13 | 27 | 38 | 49 | 65 | 76 | 97 】 |
3. 代码实现:
public class Straight_Insertion_Sort {
public static void main(String[] args){
int[] arr = {49,38,65,97,76,13,27};
int i , j;
System.out.println("初始序列:"+ Arrays.toString(arr));
//先将a[0]放入有序区,将剩下的 (arr.length - 1) 个元素放入无序区,所以循环从 i = 1开始
for( i = 1 ; i < arr.length ; i ++){
int temp = arr[i]; //每次循环将arr[i]插入到它前面已排序的子序列中
for( j = i - 1 ; j > -1 && arr[j] > temp ; j--){ //将前面较大的元素后移
arr[j+1] = arr[j];
}
arr[j+1] = temp; //temp值到达插入位置
}
System.out.println("排序后结果:"+ Arrays.toString(arr));
}
}
4. 运行结果:
初始序列:[49, 38, 65, 97, 76, 13, 27]
排序后结果:[13, 27, 38, 49, 65, 76, 97]
三、插入排序——折半插入排序
1. 基本思想:
将比较操作和移动操作分离开来,即先折半查找出元素的待插入位置,然后再统一移动插入位置之后的元素。
在有序表中查找插入位置时,可以不断二分有序表来确定插入位置,即一次比较,通过待插入记录与有序表居中的记录按关键码比较,将有序表一分为二,下次的比较操作在其中一个有序子表中进行,按同样的方法再将子表一分为二,这样继续下去,直到要比较的子表中只有一个记录时进行最后一次比较,便确定插入位置。
2. 排序过程:
| 元素下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 初始序列 | 49 | 38 | 65 | 97 | 76 | 13 | 27 |
| 第1躺排序之后 | 38 | 49 | 65 | 97 | 76 | 13 | 27 |
| 第2躺排序之后 | 38 | 49 | 65 | 97 | 76 | 13 | 27 |
| 第3躺排序之后 | 38 | 49 | 65 | 97 | 76 | 13 | 27 |
| 第4躺排序之后 | 38 | 49 | 65 | 76 | 97 | 13 | 27 |
| 第5躺排序之后 | 13 | 38 | 49 | 65 | 76 | 97 | 27 |
| 第6躺排序之后 | 13 | 27 | 38 | 49 | 65 | 76 | 97 |
3. 代码实现:
public class Binary_Insertion_Sort {
public static void main(String[] args){
int[] arr = {49,38,65,97,76,13,27};
int i , j , low , high , mid;
System.out.println("初始序列:"+ Arrays.toString(arr));
for(i = 1 ; i < arr.length ; i++){
if(arr[i] < arr[i-1]){
int temp = arr[i]; //缓存下标为i的元素
//记录搜索范围的左边界
low = 0;
//记录搜索范围的有边界
high = i - 1;
//折半确定插入位置
while(low <= high){
//记录中间位置
mid = ( low + high) / 2;
//比较中间位置数据和 i 处数据大小 , 以缩小搜索范围
if(arr[mid] > temp)
high = mid - 1;
else
low = mid + 1;
}
//将 high ~ i 处数据整体向后移动一位
for( j = i - 1 ; j > -1 && j >= high ; j--){
arr[j+1] = arr[j];
}
arr[high + 1] = temp;
}
// System.out.printf("第%d躺排序结果:",i);
// System.out.println(Arrays.toString(arr));
}
System.out.println("排序后结果:"+ Arrays.toString(arr));
}
}
4. 运行结果:
初始序列:[49, 38, 65, 97, 76, 13, 27]
排序后结果:[13, 27, 38, 49, 65, 76, 97]
四、插入排序——希尔排序
1. 基本思想:
希尔排序也成为“缩小增量排序”,其基本思想是,现将待排序的数组元素分成多个子序列,使得每个子序列的元素个数相对较少,然后对各个子序列分别进行直接插入排序,待整个待排序列“基本有序”后,最后在对所有元素进行一次直接插入排序。因此,我们要采用跳跃分割的策略:将相距某个“增量”的记录组成一个子序列,这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。希尔排序是对直接插入排序算法的优化和升级。
具体过程如下:
(1)选择一个步长序列:d1 ,d2 ,… ,di ,… dj ,… , dk ,其中 di > dj , dk=1;
(2)按步长序列个数k,对序列进行k躺排序;
(3)每趟排序,根据对应的步长 di ,将待排序列分割成若干长度为 m = n / di 或 m = n / di + 1 ,分别对各子表进行直接插入排序,仅步长因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
2. 排序过程:
不同步长的排序过程如下:
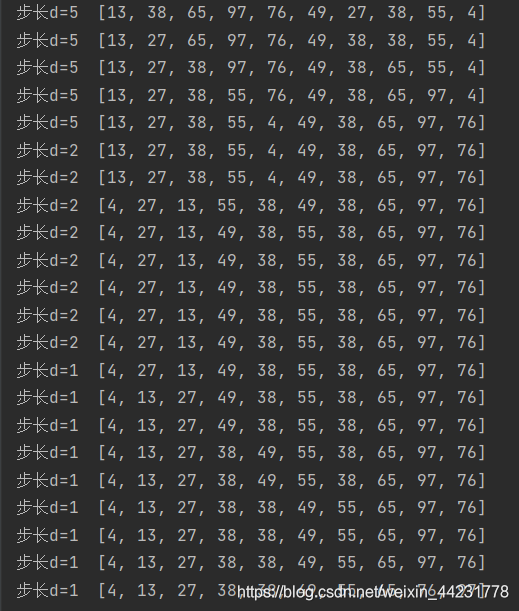
3. 代码实现:
public class Shell_Sort {
public static void main(String[] args){
int[] arr = {49,38,65,97,76,13,27,38,55,4};
int i , j , d;
System.out.println("初始序列:"+ Arrays.toString(arr));
for (d = arr.length / 2 ; d >= 1 ; d = d / 2){
for (i = d ; i < arr.length ; i++){
int temp = arr[i];
j = i - d;
while (j >= 0 && temp < arr[j]){
arr[j+d] = arr[j];
j -= d;
}
arr[j+d] = temp;
}
}
System.out.println("排序后结果:"+ Arrays.toString(arr));
}
}
4. 运行结果:
初始序列:[49, 38, 65, 97, 76, 13, 27, 38, 55, 4]
排序后结果:[4, 13, 27, 38, 38, 49, 55, 65, 76, 97]
五、算法分析
一般应从以下几方面综合考虑:1. 时间复杂度;2. 空间复杂度;3. 稳定性;4. 算法简单性; 5. 待排序记录个数;6. 记录本身信息量大小;7. 关键码分布情况。
| 排序方法 | 平均时间 | 最坏情况 | 辅助空间 | 稳定性 | 不稳定举例 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n2) | O(n2) | O(1) | 稳定 | |
| 折半插入排序 | O(n2) | O(n2) | O(1) | 稳定 | |
| 希尔排序 | O(n2) | O(n2) | O(1) | 不稳定 | 60,60’,50(d = 2,1) |