一点理解
引入
1.已知30天的消费数额,想预测第31天的数额是多少?
2.有一堆数据,每一组数据描述了一个实例,在新实例出现时描述结果是怎样?
3.早上出门天空有彩霞,半山有积云,今天会不会下雨?
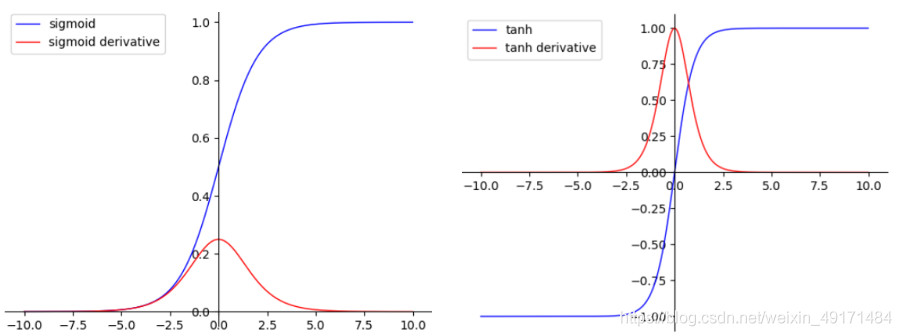
总结: 案例1 可理解为从已知数据中拟出适合的模型来预测未知数据,案例2是类似这类抽象表述,下左图即为图形化展示:f是需要设计的模型;{x1,x2,…,xn}是输入数据;w是参数,模型设计的也是求解参数,输出是一个没有范围的数值。这里理解是一个样本有n个属性{x1,x2,…,xn},不同属性赋予不同的权值,也可以表示属性的重要性。案例3即是表示的是逻辑回归案例了,输入样本的今天,属性是朝霞和半山有云2个属性,输出是只有会和不会两种结果(0和1表示),即如下右图所示。总上也可简单的理解逻辑回归和线性回归都是以未知建立模型来预测未知,只是逻辑回归是以概率形式表达,从f0到p采用的一般的概率的打分函数,有sigmoid、tanh、softmax等等,其中前两者多是二分类中使用,后一多是多分类中使用。


实例
有一组带有标签的数据分为了训练集和测试集,两种类别进行预测。
代码实现
代码实现的效果



代码片
#Step0:这里是对模型进行初始化,包括数据准备和参数初始化
clear all;clc;
data = load('train_data.txt'); #加载数据
useful_data = data;
X = useful_data(:, 2:3); #只选用第2,3列作为数据属性
y = useful_data(:, 5); #获取每个样本的标签
[m,n] = size(X);
X = [X ones(m, 1)]; #加一列1是赋予了偏置方便计算
beta = zeros(n+1, 1); #0值初始化参数
iteration = 1500; #迭代次数
alpha = 0.01; #学习率设计
#%Step1:这里进行训练获得模型
beta_tmp = [];
for iter = 1 : iteration
z = X * beta;
h = 1 ./ (1 + exp(-z));
error = h - y;
graident = X' * error;
beta = beta - alpha / m * graident;
% beta = beta*0.99 - alpha / m * graident; % momentum参数更新;
loss_value = sum(error);
beta_tmp(iter,:) = beta;
z = X*beta;
pre_tmp = sigmiod(z);
pre = [];
y_hat = y;
for i=1:size(pre_tmp,1)
if pre_tmp(i,1) <=0.5
pre(i,1) = 0;
else
pre(i,1) = 1;
end
end
count = 0;
bingo = [];
for j=1:size(pre,1)
if pre(j,1) == y_hat(j,1)
count = count+1;
bingo(count,1) = j;
end
end
train_accuracy = count./size(pre,1);
disp(['--------第', num2str(iter), '个epoch','的准确率是', num2str(train_accuracy),'--------loss_value==',num2str(loss_value)])
% 学习率进行更新;
% if i/20==0
% i = i*0.1;
% end
end
save_path = ('./batch_model.mat');
save(save_path,'beta');
save_path = ('./beta_tmp.mat');
save(save_path,'beta_tmp');
%Step2:这一步是计算训练模型下获得的准确率
beta_tmp = load('./batch_model.mat');
beta = beta_tmp.beta;
z = X*beta;
pre_tmp = sigmiod(z);
pre = [];
y_hat = y;
for i=1:size(pre_tmp,1)
if pre_tmp(i,1) <=0.5
pre(i,1) = 0;
else
pre(i,1) = 1;
end
end
count_train = 0;
bingo = [];
for j=1:size(pre,1)
if pre(j,1) == y_hat(j,1)
count_train = count_train+1;
bingo(count_train,1) = j;
end
end
train_accuracy = count./size(pre,1);
test_data_tmp = load('test_data.txt');
test_data = [test_data_tmp(:, 2:3) ones(4,1)];
test_label = [0;1;1;1];
y_test = test_data*beta;
y_test_sig = sigmiod(y_test);
pre_test = [];
for i=1:size(y_test_sig,1)
if y_test_sig(i,1) >=0.5
pre_test(i,1) = 1;
else
pre_test(i,1) = 0;
end
end
count_test = 0;
for j=1:size(pre_test,1)
if pre_test(j,1) == test_label(j,1)
count_test = count_test+1;
end
end
test_accuracy = count_test./size(pre_test,1);
%Step3:这里是对数据进行可视化
class1_train_data = data(1:19,:); %这里是对原始数据进行可视化
class0_train_data = data(20:38,:);
c1_1 = class1_train_data(:,2);
c1_2 = class1_train_data(:,3);
c1_3 = zeros(19,1);
c0_1 = class0_train_data(:,2);
c0_2 = class0_train_data(:,3);
c0_3 = zeros(19,1);
subplot(1,2,1)
scatter3(c1_1,c1_2,c1_3,'filled','r');
xlabel('x1')
ylabel('x2')
zlabel('x3')
axis manual
hold on
scatter3(c0_1,c0_2,c0_3,'filled','b');
beta_tmp = load('./batch_model.mat'); %这里下面是另外一个figure显示升维后的数据
beta = beta_tmp.beta;
c1_data = [c1_1 c1_2 ones(19,1)];
z_c1 = c1_data*beta;
c0_data = [c0_1 c0_2 ones(19,1)];
z_c0 = c0_data*beta;
scatter3(c1_1,c1_2,z_c1,'d','r');
axis manual
hold on
scatter3(c0_1,c0_2,z_c0,'p','b');
subplot(1,2,2)
x1_axis = [6:0.1:7.9];
x2_axis = [6:0.1:7.9];
x = [x1_axis' x2_axis' ones(20,1)];
y = x*beta;
xlabel('x1')
ylabel('x2')
zlabel('x3')
scatter3(c1_1,c1_2,z_c1,'d','r');
axis manual
hold on
scatter3(c0_1,c0_2,z_c0,'p','b');
axis manual %保持当前坐标刻度范围
hold on %保留图像
plot3(x1_axis,x2_axis,y,'g');
%Step4:这里是可视化loss函数
beta_tmp = load('beta_tmp.mat');
beta = beta_tmp.beta_tmp;
A = beta(1:38,:);
for i=1:38
% l = y.*(X*(beta(i,:)'/55))-log(1+exp(X*(beta(i,:)'/55)));
l = y.*(X*(beta(i,:)'))-log(1+exp(X*(beta(i,:)')));
% L(i,1) = sum(l)/10;
L(i,1) = sum(l);
end
epoch = [];
for i=1:size(A,1)
E = y.*(X*(A(i,:)'/55))-log(1+exp(X*(A(i,:)'/55)));
epoch(i,1) = sum(E)/10;
end
x = X(:,1);
y = X(:,2);
plot3(x,y,L,'r');
xlabel('x');
ylabel('y');
zlabel('z');
% scatter3(x,y,z)%散点图
% x = beta(:,1);
% y = beta(:,2);
% L = beta(:,3);
% axis manual %保持当前坐标刻度范围
hold on
[X,Y,Z]=griddata(x,y,epoch,linspace(min(x),max(x))',linspace(min(y),max(y)),'v4');
% surf(X,Y,Z);%三维曲面
meshc(X,Y,Z)