VC Is All You Need
签到题。比如在一个一维空间,有3个点,有两种颜色,你可以画一条线就可以让该线的两边都是同色。现在给你n个点,k - 1维的空间,也就相当于只能画k-1条线,能不能实现上述的分隔颜色。考虑先一个一个点地 分,最后如果剩下3个点,肯定就不能成功,所以当n > k + 1时,不存在。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
int T;
cin >> T;
while (T--)
{
ll n, k;
cin >> n >> k;
if (n > k + 1)
{
cout << "No\n";
}
else {
cout << "Yes\n";
}
}
}
Cute Tree
直接根据题意记忆化搜索,跟上次杭电的题几乎是一样的,每进去依次buildtree函数,点数加一,最后返回的是总的点数。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int ans = 0;
int d[N];
int dfs(int n)
{
if(n == 1) return (d[n] = 1);
if(n == 2) return (d[n] = 3);
if(n == 3) return (d[n] = 4);
if(d[n]) return d[n];
int mid;
if(n % 3 == 0) mid = n / 3;
else mid = n / 3 + 1;
int mid2 = (n + mid) / 2 - mid;
int mid3 = n - mid2 - mid;
return d[n] = dfs(mid) + dfs(mid2) + dfs(mid3) + 1;
}
int main()
{
int t;
cin >> t;
while(t -- )
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;i ++ ) d[i] = 0;
int t = n;
for(int i = 1;i <= n;i ++ )
{
int x;
scanf("%d",&x);
}
dfs(n);
cout << d[t] << endl;
}
return 0;
}
Banzhuan
这题其实也简单,比赛的时候也推出来了的,但是一直wa,赛后看题解也跟我们的思路是一样的,不过测了一下数据,的确不对,最后是因为取模的问题,吐了,几次都是死在取模的路上。。。最大收益的话就是每次从顶部放下,计算就行了。最小的话,先把底层填满,再沿着右上方的对角线依次填高,这样既可以保证从上方看填满了,从左方和右方也是填满的。推公式的时候注意需要用到3次方求和的公式,遇到几次了,背一下。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 1e9 + 7;
int qmi(int a, int b) {
int res = 1;
while (b) {
if (b & 1)res = (res * a) % mod;
b >>= 1;
a = (a * a) % mod;
}
return res;
}
void solve() {
int n; cin >> n;
n = n % mod;
int n1 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod)) % mod * qmi(6, mod - 2) % mod;
int n2 = n * (n + 1) % mod * qmi(2, mod - 2) % mod;
int n3 = n * n % mod;
int ma = n1 * n2 % mod * n3 % mod;
int n4 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
int n5 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod) % mod * qmi(6, mod - 2) % mod - 1 + mod) % mod;
int n6 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
int n7 = n1 * n2 % mod;
int mi = n7 + (n4 + n5) % mod * n6 % mod;
cout << mi % mod << endl << ma % mod << endl;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int T;
cin >> T;
while (T--)solve();
}
Array
这题树状数组或者分块,虽然分块暂时没看懂,看了看网上的题解,说线段树会超时,而且据说还是原题。。。这里直接给上洛谷原题的题解,https://www.luogu.com.cn/problem/solution/P4062
用树状数组维护三阶前缀和,推出公式
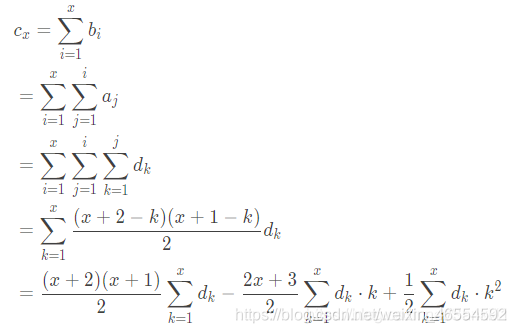
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;
const int N = 1000005;
int ans[N];
LL c1[N * 4], c2[N * 4], c3[N * 4];
LL sum(int x) {
LL res = 0;
for (int i = x; i > 0; i -= i & -i) {
res += c1[i] * (x + 2) * (x + 1) - c2[i] * (2 * x + 3) + c3[i];
}
return res / 2;
}
void add(int x, LL d, int n) {
for (int i = x; i <= n; i += i & -i) {
c1[i] += d;
c2[i] += d * x;
c3[i] += d * x * x;
}
}
int a[N];
vector<int> b[N];
int main() {
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
b[a[i]].push_back(i);
}
LL res = 0;
for (int i = 1; i <=n; i++)
{
if(ans[a[i]]==1) continue;
b[a[i]].push_back(n + 1);
int last = 0;
for (int j = 0; j < b[a[i]].size(); j++)
{
int y = 2 * j - last + N, x = 2 * j - (b[a[i]][j] - 1) + N;
res += sum(y - 1) - (x >= 3 ? sum(x - 2) : 0);
add(x, 1, 2 * N );
add(y + 1, -1, 2 * N);
last = b[a[i]][j];
}
last = 0;
for (int j = 0; j < b[a[i]].size(); j++) {
int y = 2 * j - last + N, x = 2 * j - (b[a[i]][j] - 1) + N;
add(x, -1, 2 * N);
add(y + 1, 1, 2 *N);
last = b[a[i]][j];
}
ans[a[i]]=1;
}
printf("%lld\n", res);
for(int i=1;i<=n;i++)
{
b[a[i]].clear();
ans[a[i]]=0;
}
}
//system("pause");
return 0;
}