题目

n?皇后问题研究的是如何将 n?个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的?n?皇后问题的解决方案。

每一种解法包含一个不同的?n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

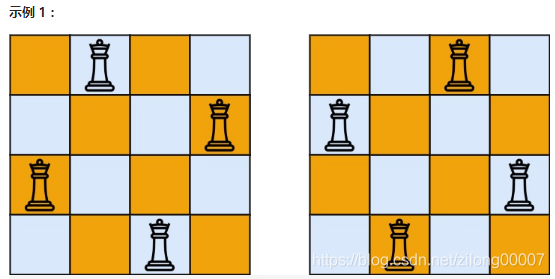
示例 1：

输入：n = 4

输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]

解释：如上图所示，4 皇后问题存在两个不同的解法

示例 2：

输入：n = 1

输出：[["Q"]]

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/n-queens

分析

这道题难度级别为困难，个人感觉它的困难不在算法，而在代码量，也可能我并没有找到好的方法，但看其他人题解也差不了多少，因为要考虑斜线，所以它的代码量有点多。

皇后之间不能相互攻击，包括X、Y轴与两斜线，所以需要四个数据结构来表示这四条线是否已经被占用，X、Y轴用boolean数组,两斜线用Set来保存。

两个格子如何判断是否在同一条斜线上呢?? 如果x坐标-y坐标值相同表示在同一条左斜线（从底部往左上）上，如果x坐标+y坐标值相同表示在同一条右斜线（从底部往右上）上。

解决了如何判断是否在同一条斜线上关键问题后，剩下的就比较简单了，使用递归+回溯就行了。

代码

class Solution {
    public List<List<String>> solveNQueens(int n) {
        boolean[] column = new boolean[n];
        boolean[] row = new boolean[n];
        Set<Integer> leftSlash = new HashSet<Integer>();
        Set<Integer> rightSlash  = new HashSet<Integer>();
        int[][] queen = new int[n][n];
        List<List<String>> res = new ArrayList<List<String>>();
        recursive(n, column, row, leftUp, rightUp, queen, res);
        return res;    
    }
    
    void recursive(int n,boolean[] column, boolean[] row, Set<Integer> leftSlash, 
                  Set<Integer> rightSlash, int[][] queen, List<List<String>> res) {
        if(n == 0){
            generator(queen, res);
            return;
        }
        
        for(int i=0;i<column.length;i++){
            int x = i;
            int y = column.length - n;
          //x-y表示左斜线， x+y表示右斜线
            if(!column[x] && !row[y] && !leftSlash.contains(x-y) && !rightSlash.contains(x+y) ){
                queen[x][y] = 1;
                column[x] = true;
                row[y] = true;
                leftSlash.add(x-y);
                rightSlash.add(x+y);
                recursive(n-1, column, row, leftSlash, rightSlash, queen, res);
                queen[x][y] = 0;
                column[x] = false;
                row[y] = false;
                leftSlash.remove(x-y);
                rightSlash.remove(x+y);
            }
        }
        
      
    }
    
    void generator(int[][] queen, List<List<String>> res) {
        List<String> list = new ArrayList<String>();
        res.add(list);
        for(int i=0;i<queen.length;i++){
            String s = "";
            for(int j=0;j<queen[i].length;j++){
                if(queen[i][j] == 1){
                    s += "Q";
                }else {
                    s += ".";
                }
               
            }
            
            list.add(s);
        }
        
    }

}