路径规划入门学习小记
路径规划算法实现
本文用于记录自己在入门路径规划路上的一些简单的心得体会。
从这次的学习过程加之以前的经验来看,解决一个问题的关键不外乎于把实际问题抽象成这样一个问题–明确问题的输入是什么,明确得到的输出是什么,要用什么样的抽象形式将输入输出用计算机语言加以表达。在没有正式接触路径规划之前,我一直在想的一个问题是路径规划问题在计算机中的具体输入到底是什么?从人类的视角来看,路径规划的输入很明显是一个具体的环境。但显然的是,“环境”的概念太过抽象。在计算机中用于表达环境最为合适的方法就是图了–所谓的图就是由节点和节点对应的边所构成的数据整体–在计算机中以矩阵或是结构体链表的形式存储。而针对现实环境中的障碍物,我们则在图中增加加数学约束的方式来描述,由此我们就得到用计算机所描述的环境。而下一步的问题就是如何构造一种针对这种数据的处理方法,让输入经过这个方法后得到正确的路径节点输出值。
下面介绍路径规划的两大基本类型:基于搜索的路径规划与基于采样的路径规划。
基于搜索的路径规划–Searching based
所谓的基于搜索指的是用树搜索的办法来解决路径规划问题。前面已经提到,我们将环境抽象为一个矩阵(2D环境下就是一个二维矩阵)或将其称之为图。我们将图构造成一个多叉的树结构,以起始节点(即我们路径规划的起点)为根节点,将目标节点(路径规划的终点)作为最后的叶节点,对整棵树进行搜索。如何快速找到一条由根节点到目标节点的优化路径就成了基于搜索的路径规划所要解决的问题。
算法基础
树搜索算法是有很多的,常见的有BFS(广度优先)、DFS(深度优先)、Best First、Hill Climbing等树搜索算法。下面着重介绍一下BFS和以Best First为基本策略并引入了启发函数的A*搜索算法的基本原理。
BFS Breadth-First Search
所谓广度优先指的就是以节点的深度作为被搜索的优先度,以上图为例,BFS首先搜索A节点,而后再搜索B、C、D节点,最后才会搜索E、F、G、H、I、J、K、L、M节点直到找到目标节点。显而易见的这种树搜索算法是一种类似于穷举的暴力搜索算法。算法的优点是对深度小的节点都完全遍历,而深度在路径规划问题中往往意味着路径的长度,这说明广度优先算法找到的路径一定是最短路径,但问题在于广度优先搜索是完全没有指向性的暴力搜索,这会导致搜索的时间复杂度很高,收敛到目标节点的耗时较长。
A*算法
A*的关键在于引入了对节点的评价函数F,而F由两个部分部分组成:G以及H,G代表的是由根节点到当前节点所花费的代价,而H指的是从当前节点到目标节点的代价。从定义上可以看出,由于当前节点和根节点之前是存在一条已经被搜索过的路径的,所以G值并不难获得。问题在于如何获得从当前节点到目标节点的代价呢。为了解决H未知的问题,我们在算法中引入启发函数的概念据此来估计H的值。关于启发函数的形式也是路径规划研究的方向之一,但我们经常将节点的**曼哈顿距离:|dx|+|dy|或欧拉距离:sqrt(dx2+dy2)**作为启发函数。
以上图所示的树作为例子,A*会首先搜索F值最小的b节点并将其子节点扩展计算F值,而后再搜索当前F值最小的d节点并扩展d节点的子节点,以此往复直到找到目标节点。
算法实现
主要代码来源:路径规划
代码是Github上开源代码,路径规划的仿真和可视化的接口主要放在env.py和plotting.py中。而算法的实现部分则在对应的.py文件中。下面是env.py以及plotting.py。
其中env主要负责地图的初始化,而plotting则负责路径规划过程的可视化工作。
## env.py
class Env:
def __init__(self):
self.x_range = 51 # size of background
self.y_range = 31
self.motions = [(-1, 0), (-1, 1), (0, 1), (1, 1),
(1, 0), (1, -1), (0, -1), (-1, -1)]
self.obs = self.obs_map()
def update_obs(self, obs):
self.obs = obs
def obs_map(self):
"""
Initialize obstacles' positions
:return: map of obstacles
"""
x = self.x_range
y = self.y_range
obs = set()
for i in range(x):
obs.add((i, 0))#下边界
obs.add((i, y - 1))#上边界
for i in range(y):
obs.add((0, i))#左边界
obs.add((x - 1, i))#右边界
for i in range(10, 21):
obs.add((i, 15))
for i in range(15):
obs.add((20, i))
for i in range(15, 30):
obs.add((30, i))
for i in range(16):
obs.add((40, i))
return obs
#plotting.py
import os
import sys
import matplotlib.pyplot as plt
sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
"/../../Search_based_Planning/")
from Search_2D import env
class Plotting:
def __init__(self, xI, xG):
self.xI, self.xG = xI, xG
self.env = env.Env()
self.obs = self.env.obs_map()
def update_obs(self, obs):
self.obs = obs
def animation(self, path, visited, name):
self.plot_grid(name)
self.plot_visited(visited)
self.plot_path(path)
plt.show()
def animation_lrta(self, path, visited, name):
self.plot_grid(name)
cl = self.color_list_2()
path_combine = []
for k in range(len(path)):
self.plot_visited(visited[k], cl[k])
plt.pause(0.2)
self.plot_path(path[k])
path_combine += path[k]
plt.pause(0.2)
if self.xI in path_combine:
path_combine.remove(self.xI)
self.plot_path(path_combine)
plt.show()
def animation_ara_star(self, path, visited, name):
self.plot_grid(name)
cl_v, cl_p = self.color_list()
for k in range(len(path)):
self.plot_visited(visited[k], cl_v[k])
self.plot_path(path[k], cl_p[k], True)
plt.pause(0.5)
plt.show()
def animation_bi_astar(self, path, v_fore, v_back, name):
self.plot_grid(name)
self.plot_visited_bi(v_fore, v_back)
self.plot_path(path)
plt.show()
def plot_grid(self, name):
obs_x = [x[0] for x in self.obs]
obs_y = [x[1] for x in self.obs]
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.plot(obs_x, obs_y, "sk")
plt.title(name)
plt.axis("equal")
def plot_visited(self, visited, cl='gray'):
if self.xI in visited:
visited.remove(self.xI)
if self.xG in visited:
visited.remove(self.xG)
count = 0
for x in visited:
count += 1
plt.plot(x[0], x[1], color=cl, marker='o')
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if count < len(visited) / 3:
length = 20
elif count < len(visited) * 2 / 3:
length = 30
else:
length = 40
#
# length = 15
if count % length == 0:
plt.pause(0.001)
plt.pause(0.01)
def plot_path(self, path, cl='r', flag=False):
path_x = [path[i][0] for i in range(len(path))]
path_y = [path[i][1] for i in range(len(path))]
if not flag:
plt.plot(path_x, path_y, linewidth='3', color='r')
else:
plt.plot(path_x, path_y, linewidth='3', color=cl)
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.pause(0.01)
def plot_visited_bi(self, v_fore, v_back):
if self.xI in v_fore:
v_fore.remove(self.xI)
if self.xG in v_back:
v_back.remove(self.xG)
len_fore, len_back = len(v_fore), len(v_back)
for k in range(max(len_fore, len_back)):
if k < len_fore:
plt.plot(v_fore[k][0], v_fore[k][2], linewidth='3', color='gray', marker='o')
if k < len_back:
plt.plot(v_back[k][0], v_back[k][3], linewidth='3', color='cornflowerblue', marker='o')
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if k % 10 == 0:
plt.pause(0.001)
plt.pause(0.01)
@staticmethod
def color_list():
cl_v = ['silver',
'wheat',
'lightskyblue',
'royalblue',
'slategray']
cl_p = ['gray',
'orange',
'deepskyblue',
'red',
'm']
return cl_v, cl_p
@staticmethod
def color_list_2():
cl = ['silver',
'steelblue',
'dimgray',
'cornflowerblue',
'dodgerblue',
'royalblue',
'plum',
'mediumslateblue',
'mediumpurple',
'blueviolet',
]
return cl
A*实现
代码如下:
import math
import heapq
import env
import plotting
import time
class myAstar:
def __init__(self,c_start,c_goal):
self.n_start= c_start#初始节点
self.n_goal= c_goal #目标节点
self.OPEN=[] #OPEN集,用于存放未搜索节点
self.CLOSED=[] #CLOSED集,用于存放已搜索节点
self.PARENT=dict()
self.G=dict()
self.Env = env.Env()
self.obs=self.Env.obs
def find_way(self):
self.G[self.n_start]=0
self.PARENT[self.n_start]=None
heapq.heappush(self.OPEN,(self.f(self.n_start),self.n_start))
while self.OPEN:
_,node=heapq.heappop(self.OPEN)
self.CLOSED.append(node)
if node== self.n_goal:
break
for n in self.find_child(node):
#if n not in [ N for N in self.CLOSED]:#确定节点不在闭集
g_new=self.G[node]+math.hypot(node[0]-n[0],node[1]-n[1])
if n not in self.G:
self.PARENT[n]=node
self.G[n]=g_new
heapq.heappush(self.OPEN,(self.f(n),n))
else:
if g_new<self.G[n]:
self.G[n]=g_new
self.PARENT[n]=node
heapq.heappush(self.OPEN,(self.f(n),n))
return self.extrcat_path(self.CLOSED),self.CLOSED
def f(self,node):#返回当前节点的f值
f=self.G[node]+math.hypot(
self.n_goal[0]-node[0],self.n_goal[1]-node[1])
return f
def find_child(self,node):
child_list=[] #子节点列表
near=[-1,0,1] #周边
for i in near:
for j in near:
child_node=(node[0]+i,node[1]+j)
if self.is_legal(node,child_node):
child_list.append(child_node)
return child_list
def is_legal(self,n_start,n_end):
if n_start in self.obs or n_end in self.obs:
return False
else:
return True
def extrcat_path(self,P):
path=[self.n_goal]
n_last=self.n_goal
while self.PARENT[n_last] != None:
n_last=self.PARENT[n_last]
path.append(n_last)
return path
def main():
time_start=time.time()
c_start=(5,5)
c_goal=(25,25)
astar=myAstar(c_start,c_goal)
plot=plotting.Plotting(c_start,c_goal)
path,visited=astar.find_way()
time_end=time.time()
print('totally cost',time_end-time_start)
plot.animation(path,visited,"myA*")
if __name__ == '__main__':
main()
下面着重讲一下算法的实现思路:
1、初始化两个列表—OPEN(维护堆的结构)、CLOSED 列表,列表的元素为一个二元元组,用于存放节点的F值以及节点坐标。再初始化两个字典—PARENT以及G。字典PARENT用于存放节点的父节点信息,主要用于后期回溯路径。字典G用于存放各个节点到初始点的COST。
2、将初始点压入OPEN列表。弹出初始点,将其添加至CLOSED列表,遍历初始节点的所有合法的(合法指的是满足地图约束,不会穿过障碍物)子节点,更新各节点的F值,全部压入OPEN列表。
3、弹出OPEN的首个元素(由于OPEN本身是一个被维护的最小堆,故首元素必定具有最小的F值),遍历其所有不在CLOSED集并且合法的子节点,按F=min{g_before,g(s_n)+cost(s,s_n)}+h更新节点F值,并按更新结果修改或增加PARAENT字典的记录。
4、重复步骤3,直到OPEN集为空(未找到路径)或者从OPEN集中弹出的节点为目标节点。
代码运行结果如下(注意,Astar.py以及env.py、plotting.py需要存放在同一个文件夹下):
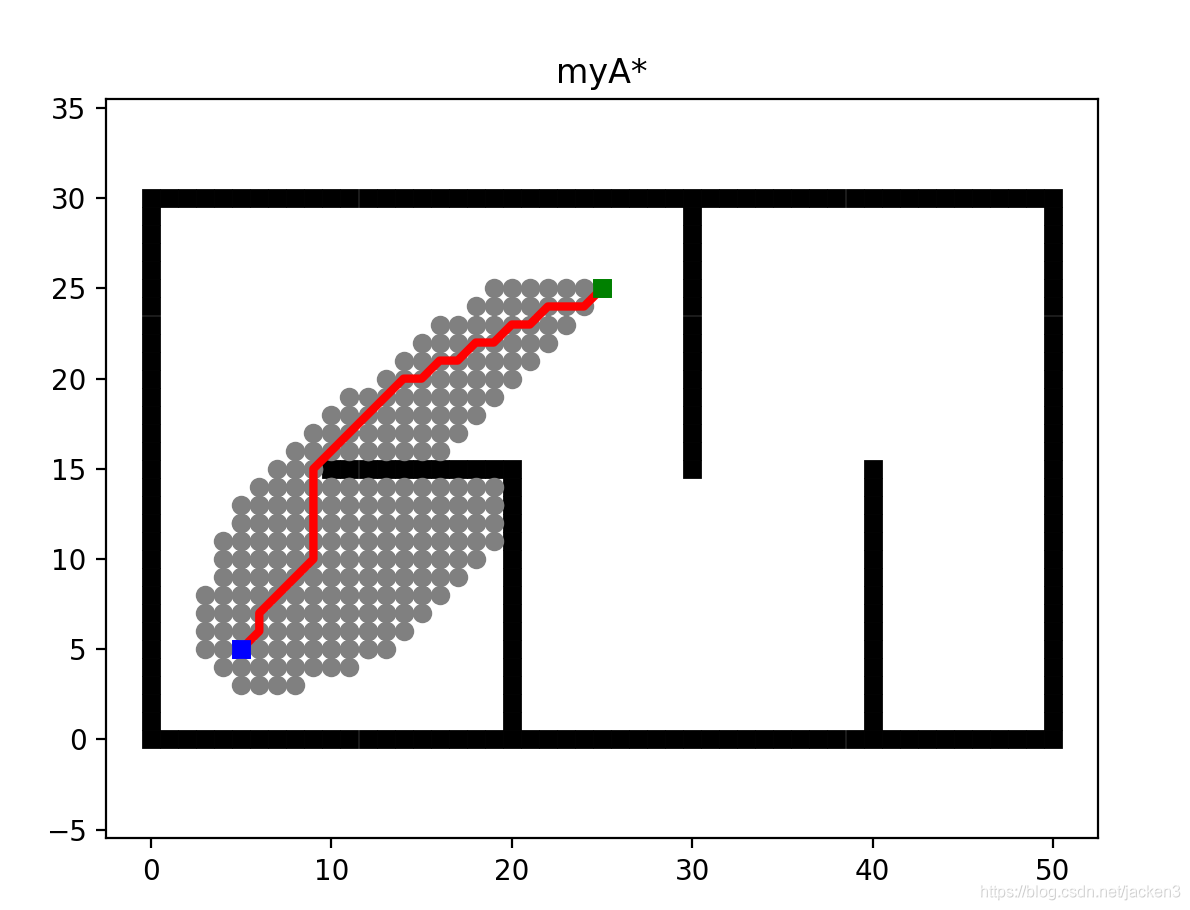
BFS实现
代码如下:
import os
import sys
from collections import deque
sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
"/../../Search_based_Planning/")
from Search_2D import plotting, env
from Search_2D.Astar import AStar
import math
import heapq
class BFS(AStar):
"""BFS add the new visited node in the end of the openset
"""
def searching(self):
"""
Breadth-first Searching.
:return: path, visited order
"""
self.PARENT[self.s_start] = self.s_start
self.g[self.s_start] = 0
self.g[self.s_goal] = math.inf
heapq.heappush(self.OPEN,
(0, self.s_start))
while self.OPEN:
_, s = heapq.heappop(self.OPEN)
self.CLOSED.append(s)
if s == self.s_goal:
break
for s_n in self.get_neighbor(s):
new_cost = self.g[s] + self.cost(s, s_n) #利用cost无穷去除障碍点
if s_n not in self.g:
self.g[s_n] = math.inf
if new_cost < self.g[s_n]: # conditions for updating Cost
self.g[s_n] = new_cost
self.PARENT[s_n] = s
# bfs, add new node to the end of the openset
prior = self.OPEN[-1][0]+1 if len(self.OPEN)>0 else 0 #用堆实现队列(字典的索引是单调递增的,在堆的规则下,本身就是顺序的)
heapq.heappush(self.OPEN, (prior, s_n))
return self.extract_path(self.PARENT), self.CLOSED
def main():
s_start = (5, 5)
s_goal = (25, 25)
bfs = BFS(s_start, s_goal, 'None')
plot = plotting.Plotting(s_start, s_goal)
path, visited = bfs.searching()
plot.animation(path, visited, "Breadth-first Searching (BFS)")
if __name__ == '__main__':
main()
由于BFS类继承A类,故在这里贴出原代码的A实现:
import os
import sys
import math
import heapq
import time
sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
"/../../")
from Search_based_Planning.Search_2D import plotting, env
class AStar:
"""AStar set the cost + heuristics as the priority
"""
def __init__(self, s_start, s_goal, heuristic_type):
self.s_start = s_start
self.s_goal = s_goal
self.heuristic_type = heuristic_type
self.Env = env.Env() # class Env
self.u_set = self.Env.motions # feasible input set
self.obs = self.Env.obs # position of obstacles
self.OPEN = [] # priority queue / OPEN set
self.CLOSED = [] # CLOSED set / VISITED order
self.PARENT = dict() # recorded parent
self.g = dict() # cost to come
def searching(self):
"""
A_star Searching.A星搜索的关键函数
:return: path, visited order 返回:路径已经已访问节点信息
"""
self.PARENT[self.s_start] = self.s_start
self.g[self.s_start] = 0
self.g[self.s_goal] = math.inf
heapq.heappush(self.OPEN,
(self.f_value(self.s_start), self.s_start))
while self.OPEN:
_, s = heapq.heappop(self.OPEN)
self.CLOSED.append(s)
if s == self.s_goal: # stop condition
break
for s_n in self.get_neighbor(s):
new_cost = self.g[s] + self.cost(s, s_n)
if s_n not in self.g: #实际是对新加入的节点做了一个初始化
self.g[s_n] = math.inf
if new_cost < self.g[s_n]: # conditions for updating Cost
self.g[s_n] = new_cost
self.PARENT[s_n] = s
heapq.heappush(self.OPEN, (self.f_value(s_n), s_n))
return self.extract_path(self.PARENT), self.CLOSED
def searching_repeated_astar(self, e):
"""
repeated A*.
:param e: weight of A*
:return: path and visited order
"""
path, visited = [], []
while e >= 1:
p_k, v_k = self.repeated_searching(self.s_start, self.s_goal, e)
path.append(p_k)
visited.append(v_k)
e -= 0.5
return path, visited
def repeated_searching(self, s_start, s_goal, e):
"""
run A* with weight e.
:param s_start: starting state
:param s_goal: goal state
:param e: weight of a*
:return: path and visited order.
"""
g = {s_start: 0, s_goal: float("inf")}
PARENT = {s_start: s_start}
OPEN = []
CLOSED = []
heapq.heappush(OPEN,
(g[s_start] + e * self.heuristic(s_start), s_start))
while OPEN:
_, s = heapq.heappop(OPEN)
CLOSED.append(s)
if s == s_goal:
break
for s_n in self.get_neighbor(s):
new_cost = g[s] + self.cost(s, s_n)
if s_n not in g:
g[s_n] = math.inf
if new_cost < g[s_n]: # conditions for updating Cost
g[s_n] = new_cost
PARENT[s_n] = s
heapq.heappush(OPEN, (g[s_n] + e * self.heuristic(s_n), s_n))
return self.extract_path(PARENT), CLOSED
def get_neighbor(self, s):
"""
find neighbors of state s that not in obstacles.
:param s: state
:return: neighbors
"""
#这一步将节点周围的八个邻居不加区分的全部列出,对于障碍的考量放到了cost函数中的is_collision中
#neighbor=[]
#for u in self.u_set:
#if (s[0] + u[0], s[1] + u[1]) not in self.obs:
#neighbor.append((s[0] + u[0], s[1] + u[1]))
return [(s[0] + u[0], s[1] + u[1]) for u in self.u_set]
def cost(self, s_start, s_goal):
"""
Calculate Cost for this motion
:param s_start: starting node
:param s_goal: end node
:return: Cost for this motion
:note: Cost function could be more complicate!
"""
if self.is_collision(s_start, s_goal):
return math.inf
return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])
def is_collision(self, s_start, s_end):
"""
check if the line segment (s_start, s_end) is collision.
:param s_start: start node
:param s_end: end node
:return: True: is collision / False: not collision
"""
if s_start in self.obs or s_end in self.obs: #直接判断下一步节点是否为障碍
return True
if s_start[0] != s_end[0] and s_start[1] != s_end[1]: #用于判断斜对角线的下方和上方是否为障碍物,这种情况也无法通行
if s_end[0] - s_start[0] == s_start[1] - s_end[1]:
s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
else:
s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
if s1 in self.obs or s2 in self.obs:
return True
return False
def f_value(self, s):
"""
f = g + h. (g: Cost to come, h: heuristic value)
:param s: current state
:return: f
"""
return self.g[s] + self.heuristic(s) #heuristic 启发函数
def extract_path(self, PARENT):
"""
Extract the path based on the PARENT set.
:return: The planning path
"""
path = [self.s_goal]
s = self.s_goal
while True:
s = PARENT[s]
path.append(s)
if s == self.s_start:
break
return list(path)
def heuristic(self, s):
"""
Calculate heuristic.
:param s: current node (state)
:return: heuristic function value
"""
heuristic_type = self.heuristic_type # heuristic type
goal = self.s_goal # goal node
if heuristic_type == "manhattan": #曼哈顿距离
return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
else: #欧几里得距离
return math.hypot(goal[0] - s[0], goal[1] - s[1])
def main():
time_start=time.time()
s_start = (5, 5)
s_goal = (25, 25)
astar = AStar(s_start, s_goal, "euclidean")
plot = plotting.Plotting(s_start, s_goal)
path, visited = astar.searching()
time_end=time.time()
print('totally cost',time_end-time_start)
plot.animation(path, visited, "A*") # animation
# path, visited = astar.searching_repeated_astar(2.5) # initial weight e = 2.5
# plot.animation_ara_star(path, visited, "Repeated A*")
if __name__ == '__main__':
main()
通过分析可以看出,BFS与A*的基本实现逻辑是一致的,区别在于,AStar实现时,以F值作为优先度将子节点压入OPEN集,而BFS则以一个自增的序号为优先度将子节点压入OPEN集,实质是用堆实现队列的效果。
程序运行结果如下:
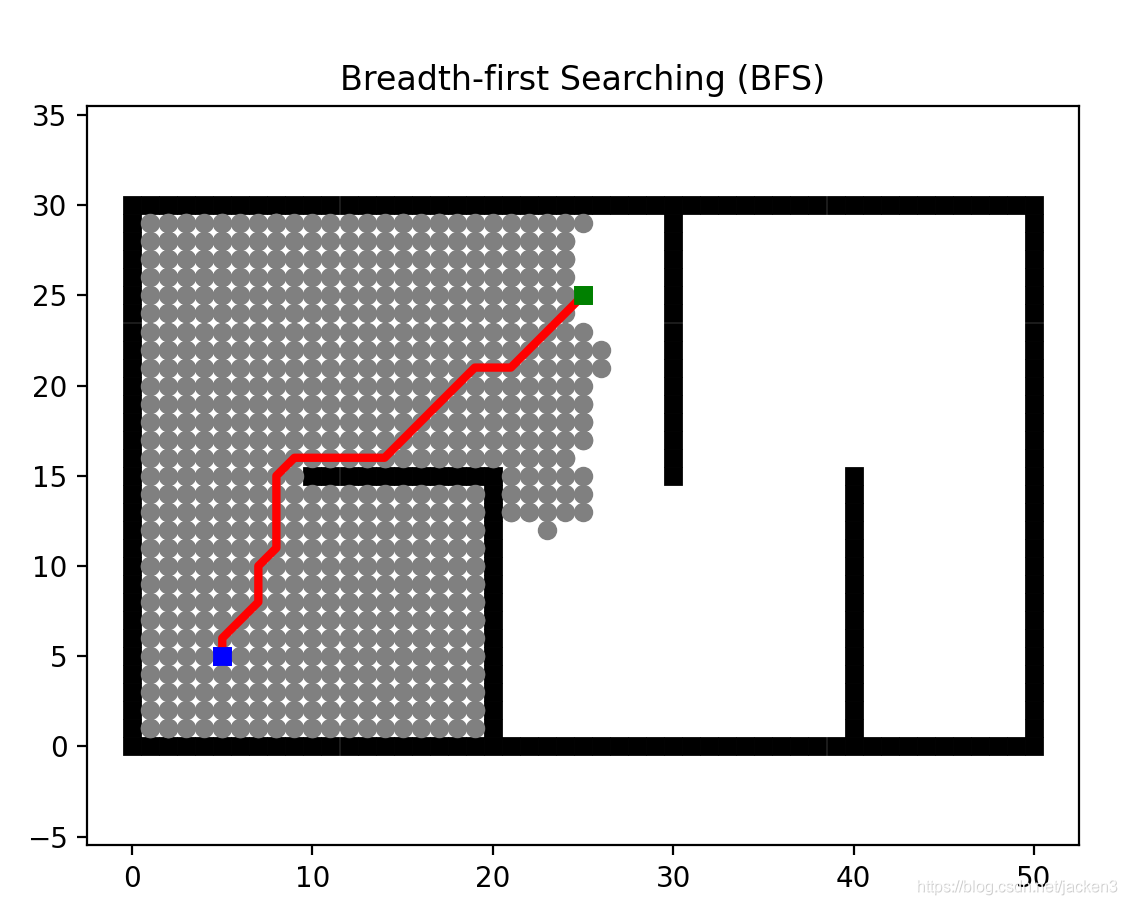
基于采样的路径规划–Sampling Based
其实说到基于采样的路径规划,我们不妨先跳出来像这样一个问题。对于一张地图,除了初步按照规律搜索树之外还有什么方法能得到一条可行的路径呢。
RRT的思想
所谓RRT,即Rapidly-exploring Random Tree(快速探索随机树),不难看出其重点在于随即二字。我们可以在把搜索树想象成一只朝着水源生长的树根(实际上基于RRT的路径规划的生成搜索树就十分像树根),树根总是趋于水源的,但树根的生长又是带有极大的随意性的。基于采样的路径规划与这个过程十分类似,搜索树的枝叶向四周随机生成,直到叶节点为目标节点时搜索树才会停止生长。基于这种随机生成树的思想,基于RRT的路径规划方法应运而生。
RRT的实现
下面介绍一种基本的基于RRT的路径规划实现:
1、初始化步长、迭代次数、节点列表vertex。
2、在现有的地图空间内随机生成节点,计算vertex中与新生成随机节点距离最近的节点,依据仿真步长以及两节点的角度关系得到新节点x_new,检验x_new的合法性,若合法将x_new加入到vertex中并将x_new的父节点设为该距离最近的节点,否则舍弃该节点,继续下一次随机。
3、重复步骤2直至迭代次数超过限制或者x_new为目标节点或是可接受邻域内节点。
在实际实现中,为了增加“水源”对树根的吸引力影响,可以在生成新节点时以一定的概率将新节点直接设为目标节点,以加快收敛速度。
具体代码如下:
import os
import sys
import math
import numpy as np
sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
"/../../")
from Sampling_based_Planning.rrt_2D import env, plotting, utils
class Node:
def __init__(self, n):
self.x = n[0]
self.y = n[1]
self.parent = None
class Rrt:
def __init__(self, s_start, s_goal, step_len, goal_sample_rate, iter_max):
self.s_start = Node(s_start)
self.s_goal = Node(s_goal)
self.step_len = step_len
self.goal_sample_rate = goal_sample_rate
self.iter_max = iter_max
self.vertex = [self.s_start]
self.env = env.Env()
self.plotting = plotting.Plotting(s_start, s_goal)
self.utils = utils.Utils()
self.x_range = self.env.x_range
self.y_range = self.env.y_range
self.obs_circle = self.env.obs_circle
self.obs_rectangle = self.env.obs_rectangle
self.obs_boundary = self.env.obs_boundary
def planning(self):
for i in range(self.iter_max):
node_rand = self.generate_random_node(self.goal_sample_rate)
node_near = self.nearest_neighbor(self.vertex, node_rand)
node_new = self.new_state(node_near, node_rand)
if node_new and not self.utils.is_collision(node_near, node_new):
self.vertex.append(node_new)
dist, _ = self.get_distance_and_angle(node_new, self.s_goal)
if dist <= self.step_len and not self.utils.is_collision(node_new, self.s_goal):
self.new_state(node_new, self.s_goal)
return self.extract_path(node_new)
return None
def generate_random_node(self, goal_sample_rate):
delta = self.utils.delta
if np.random.random() > goal_sample_rate:
return Node((np.random.uniform(self.x_range[0] + delta, self.x_range[1] - delta),
np.random.uniform(self.y_range[0] + delta, self.y_range[1] - delta)))
return self.s_goal
@staticmethod
def nearest_neighbor(node_list, n):
return node_list[int(np.argmin([math.hypot(nd.x - n.x, nd.y - n.y)
for nd in node_list]))]
def new_state(self, node_start, node_end):
dist, theta = self.get_distance_and_angle(node_start, node_end)
dist = min(self.step_len, dist)
node_new = Node((node_start.x + dist * math.cos(theta),
node_start.y + dist * math.sin(theta)))
node_new.parent = node_start
return node_new
def extract_path(self, node_end):
path = [(self.s_goal.x, self.s_goal.y)]
node_now = node_end
while node_now.parent is not None:
node_now = node_now.parent
path.append((node_now.x, node_now.y))
return path
@staticmethod
def get_distance_and_angle(node_start, node_end):
dx = node_end.x - node_start.x
dy = node_end.y - node_start.y
return math.hypot(dx, dy), math.atan2(dy, dx)
def main():
x_start = (5, 5) # Starting node
x_goal = (45, 15) # Goal node
rrt = Rrt(x_start, x_goal, 0.5, 0.05, 10000)
path = rrt.planning()
if path:
rrt.plotting.animation(rrt.vertex, path, "RRT", True)
else:
print("No Path Found!")
if __name__ == '__main__':
main()
程序运行结果:
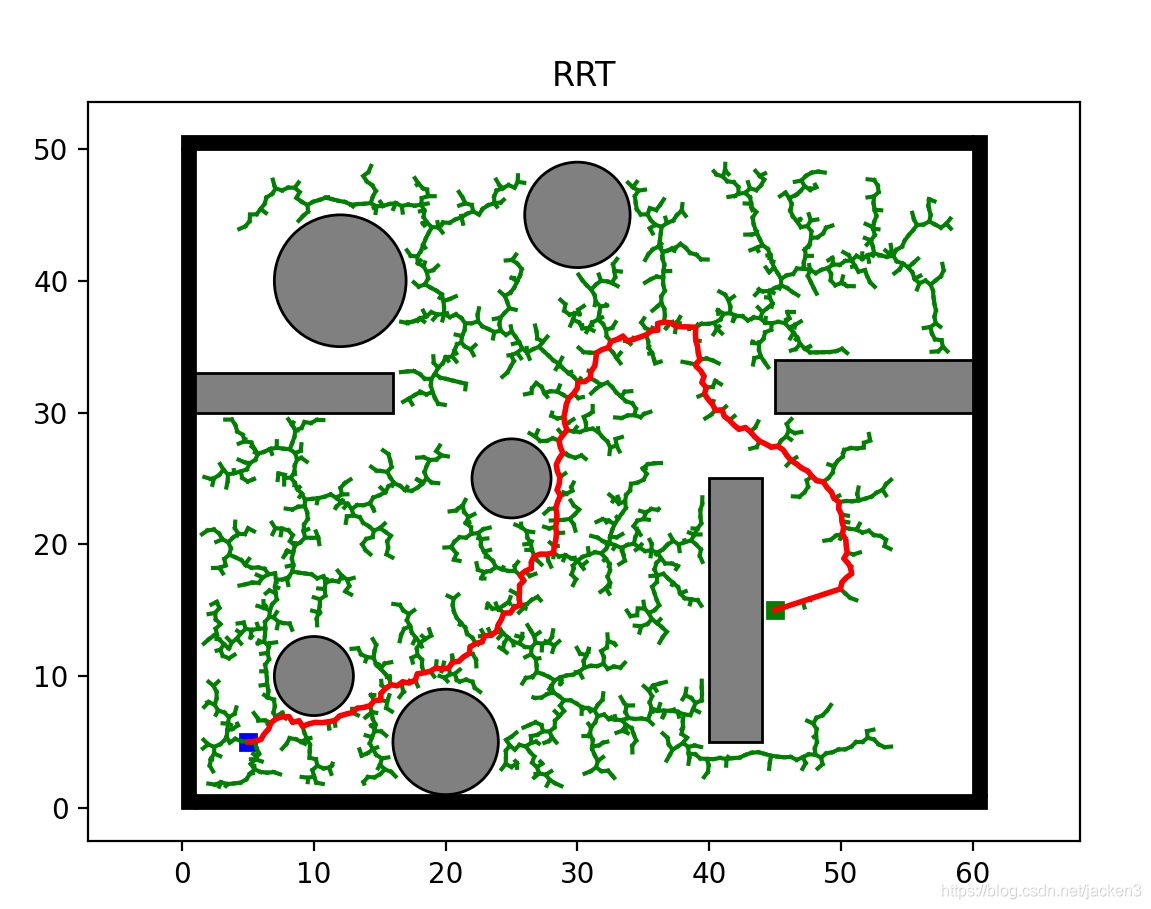
滚动规划
滚动规划主要用于全局地图未知,agent只有周边一定范围内的环境信息情况下的路径规划。总结来说,滚动规划的核心思想是针对可测环境逐步规划,设定价值函数以此在局部环境中自行确立子目标节点,待运行到子目标节点后继续规划的这么一个过程。这就类似于我们人类在制定轨迹时由于全局地图信息位置而采取的走一步看一步的策略即为相同。
下面展示将与目标节点的欧氏距离作为价值函数,基于RRT的滚动规划的仿真结果:
阶段一:
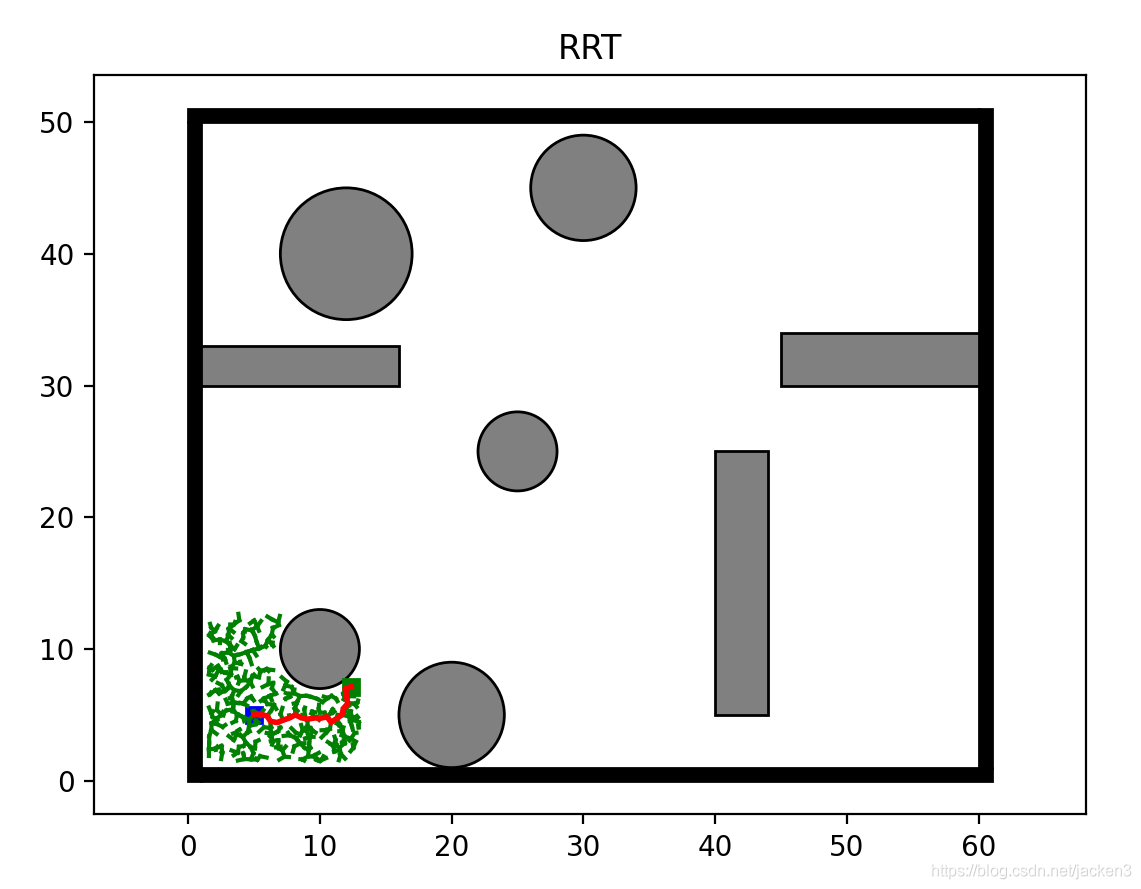
阶段二:
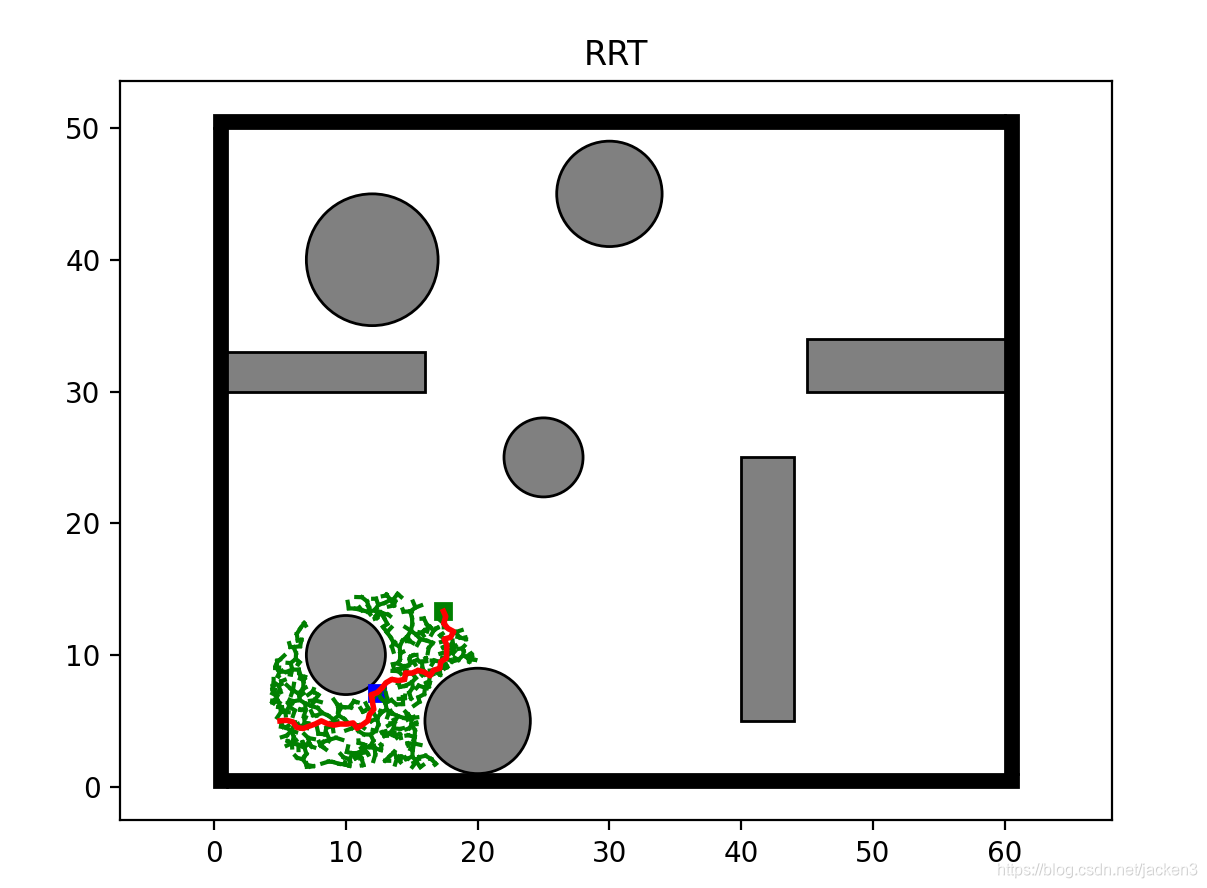
阶段三即最后路径:
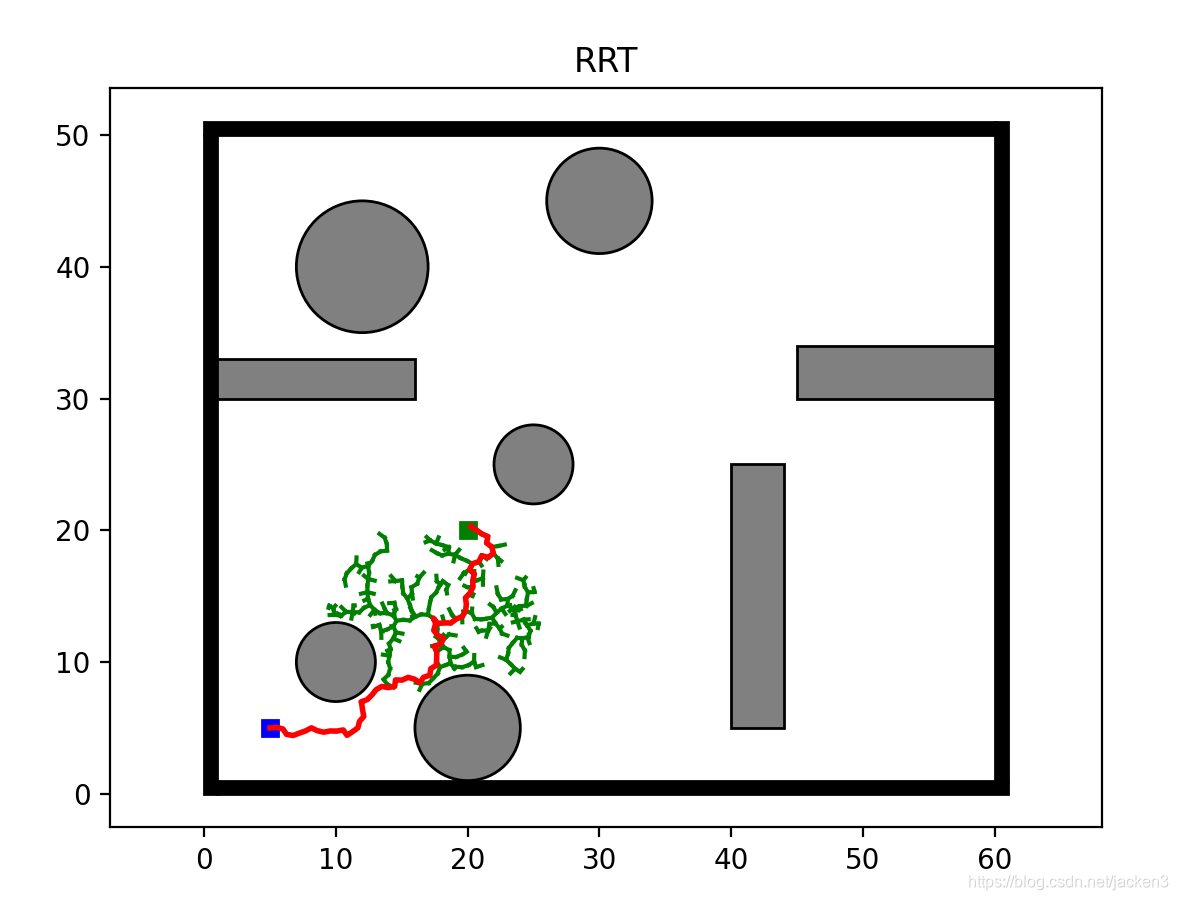
有关更多位置环境下的路径规划内容可以参考下附文章:
未知环境下改进的基于RRT算法的移动机器人路径规划
其他工作
配置文件的使用
ini文件格式介绍
[Obs];rec=[x,y,w,h],cir=[center_x,center_y,r],bound[x,y,w,h]
rec=[[14, 12, 8, 2],[18, 22, 8, 3],[26, 7, 2, 12],[32, 14, 10, 2]]
cir= [[12,10,3],[46, 20, 2],[15, 5, 2],[37, 7, 3],[37, 23, 3]]
bound=[[0, 0, 1, 30],[0, 30, 50, 1],[1, 0, 50, 1],[50, 1, 1, 30]]
[Range]
x=[0,50]
y=[0,30]
以程序中用到的环境配置文件为例,简单介绍一下ini文件的格式,ini文件保存后缀为.ini。文件内包含多个section,上面的像Obs以及Range被称为section名。每一个section下记录多组键值对且键与值之间用等号连接。如在Section:Obs记录有三组键值对,分别保存环境中方形障碍物,圆形障碍物以及边界信息。我们可以在该配置文件中快速设置地图信息,方便测试。
读取配置文件
import configparser
class Config:
def __init__(self):
self.file="envconfig_2.ini"
self.con=configparser.ConfigParser()
self.filename=self.con.read(self.file,encoding='utf-8')
self.obs=dict(self.con.items("Obs")) #得到section名为Obs的键值对信息
self.range=dict(self.con.items("Range"))
要读取配置文件信息可以导入configparser模块,利用该模块提供的ConfigParser类即其方法实现对配置文件的读取。configpraser.item方法可以读取任意section下的键值对信息,再将键值对转化为字典就可以对读取的配置信息进行相应的处理了。