[数据结构与算法]数据结构树

树的定义

线性结构:第一个数元素无前驱,最后一个数据元素无后继,中间节点一个前驱,一个后继
树结构: 根节点无双亲,叶节点无孩子,中间节点一个双亲,多个孩子

树的存储结构

双亲表示法

每个节点有一个data存储数据信息,一个parent存储双亲结点的下标

/*双亲表示法存储结构 parent*/
#define MAXSIZE 100
typedef int TElemType;

typedef struct PTNode
{
	TElemType data;
	int parent;
}PTNode;
typedef struct
{
	PTNode node[MAXSIZE];
	int r;    //根的位置
	int n;    //节点数量
}PTree;

很容易找到双亲节点;若要找它的孩子节点,需要遍历整棵树

孩子节点表示法

方案一:
指针域的个数等于树的度


这种存储对孩子节点数量相差比较大的比较浪费存储空间,好多都为空
方案二:
按照指针个数等于树的度,我们设置一个degree来存储每个节点的孩子数量


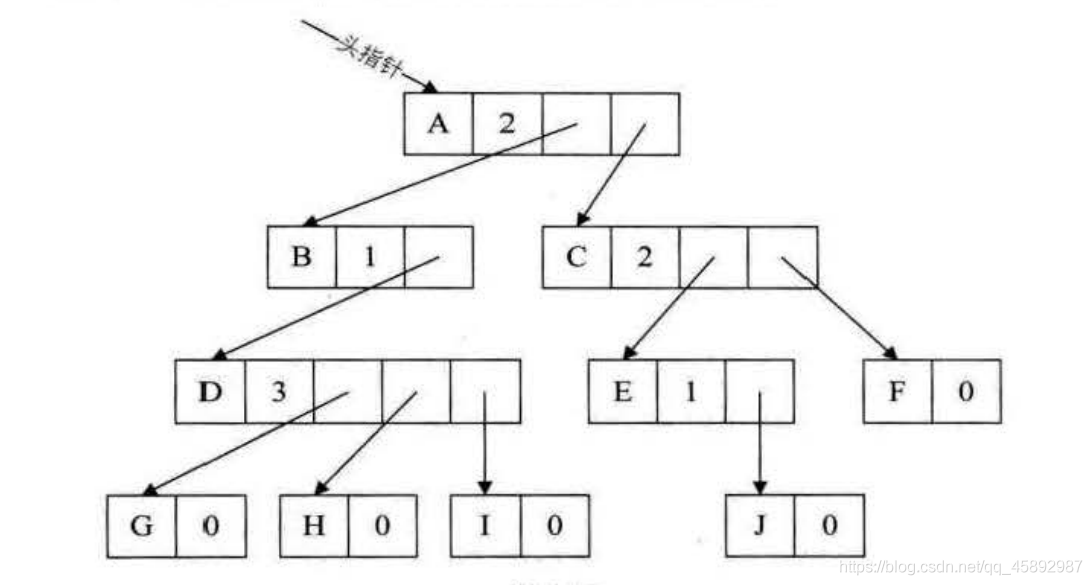
这种存储克服了对空间的浪费,但是每个结点的结构又不相同了
方案三:
每个结点的孩子以单链表的形式连接起来

/*树的孩子表示法结构定义*/

typedef struct CTNode //孩子结点
{
	int child;
	struct CTNode * next;
}*ChildPtr;
typedef struct  //表头结构
{
	TElemType data;
	ChildPtr firstChild;
}CTBox;
typedef struct  //树结构
{
	CTBox node[MAXSIZE];
	int r;    //根的下标
	int n;    //结点的数量
}CTree;

该存储结构对于查找孩子结点只需要遍历单链表即可,但对于查找双亲结点有点困难(可以在结点中加一个存储双亲结点的变量)

孩子兄弟表示法

/*树的孩子兄弟表示法*/
typedef struct CSNode
{
	TElemType data;
	struct CSNode * firstChild;
	struct CSNode * rightSib;
}CSNode,*CSTree;

把一颗复杂的树变成了二叉树

二叉树

存储结构

/*二叉树的二叉链表存储结构*/
typedef struct BiNode
{
	TElemType data;
	struct BiNode * lChild;
	struct BiNode * rChild;
}BiNode,*BiTree;

遍历

前序

/*二叉树的前序遍历递归算法*/
void PreOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	printf("%d ", T->data);
	PreOrderTraverse(T->lChild);
	PreOrderTraverse(T->rChild);
}

中序

/*二叉树的中序遍历递归算法*/
void InOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	InOrderTraverse(T->lChild);
	printf("%d ", T->data);
	InOrderTraverse(T->rChild);
}

后序

/*二叉树的后序遍历递归算法*/
void PostOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	PostOrderTraverse(T->lChild);
	PostOrderTraverse(T->rChild);
	printf("%d ", T->data);
}

建立二叉树

/*按照前序建立二叉树*/
void CreateBiTree(BiTree * T)
{
	TElemType ch;
	scanf("%c", &ch);
	if (ch == '#')
	{
		*T = NULL;
	}
	else
	{
		*T = (BiTree)malloc(sizeof(BiNode));
		(*T)->data = ch;
		CreateBiTree(&(*T)->lChild);
		CreateBiTree(&(*T)->rChild);
	}
}

线索二叉树

存储结构

/*二叉树的的线索存储结构*/
typedef enum 
{
	Link,   //0 指向左右孩子指针
	Thread  //1 指向前驱或后继指针
}PointerTag;
typedef struct BiThrNode
{
	TElemType data;
	struct BiThrNode * lChild;
	struct BiThrNode * rChild;
	PointerTag lTag; //左标志
	PointerTag rTag; //右标志
}BiThrNode,*BiThrTree;

线索化

/*中序的线索二叉*/
BiThrTree pre; //始终指向访问过的结点
void InThreading(BiThrTree p)
{
	if (p)
	{
		InThreading(p->lChild);

		if (!p->lChild)
		{
			p->lTag = Thread;
			p->lChild = pre;
		}

		if (!pre->rChild)
		{
			pre->rTag = Thread;
			pre->rChild = p;
		}
		pre = p;

		InThreading(p->rChild);
	}
}

中序遍历

/* 中序遍历线索二叉*/
void InOrderTraverse(BiThrTree T)
{
	BiThrTree p;
	p = T->lChild;
	while (p != T)
	{
		while (p->lTag == Link)
		{
			p = p->lChild;
		}
		printf("%c", p->data);
		while (p->rTag == Thread && p->rChild != T)
		{
			p = p->rChild;
			printf("%c", p->data);
		}
		p = p->rChild;

	}
}