前言
如果存在什么奇怪的问题
1.压缩包放到linux环境下再解压,并且不要放共享文件夹里做
2.不建议使用wsl1和wsl2
英文水平有限以及对cache理解命中率优化有限参考了现有网上很多大佬的题解
以及这个实验是有一份ppt的,这份ppt里面介绍了两个模拟要用的库函数。
ppt链接:http://www.cs.cmu.edu/afs/cs/academic/class/15213-f15/www/recitations/rec07.pdf
PartA
要求我们模拟cache的行为,函数写在csim.c里面。
实现以下功能。
Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile>
? -h: Optional help flag that prints usage info
? -v: Optional verbose flag that displays trace info
? -s <s>: Number of set index bits (S = 2s
is the number of sets)
? -E <E>: Associativity (number of lines per set)
? -b <b>: Number of block bits (B = 2b
is the block size)
? -t <tracefile>: Name of the valgrind trace to replay刚看到是有点懵逼。
这就是一个字符串的读入,读入的内容在文件里面,所以要main要重定向进行流输入。(getopt)
数据的读入
上面的代码部分就是界面。
1.这次实验只要求我们测试hit/miss/eviction的次数,并没有实际的数据存储?,所以我们不用实现line中的block部分。
2.实验要求使用LRU替换策略
考虑模拟的结构:
1.cache的结构体:组,行,块。动态分配空间,结束时候释放。
2.读入二进制流后获得本次操作的信息,是否打印输出,cache的信息,每次输入数据的文件
3.初始化完cache后准备输入数据的文件进行cache的处理
4.cache的处理部分有查找,命中与不命中,以及不命中时候使用LRU替换策略
#include "cachelab.h"
#include <unistd.h>
#include <stdio.h>
#include <getopt.h>
#include <stdlib.h>
/*要打印的答案*/
long long hit_count,miss_count,eviction_count;
int output;
/*定义cache的结构*/
struct Line{
int valid;
long long s_add;
unsigned long LRU_counter;
};
struct Group{
struct Line* lines;
};
struct Cache{
long long s;
long long E;
long long b;
struct Group* groups;
};
/*初始化cache*/
struct Cache initCache(long long s,long long E,long long b){
struct Cache cache;
cache.s=s;cache.E=E;cache.b=b;
long long S=1<<s;
cache.groups=(struct Group*)malloc( S*sizeof(struct Group) );
for(int i=0;i<S;i++){
cache.groups[i].lines=(struct Line*)malloc(E *sizeof(struct Line) );
}
return cache;
}
void release(struct Cache cache){
long long S=1<<cache.s;
for(long long i=0;i<S;i++){
free(cache.groups[i].lines);
}
free(cache.groups);
}
/*LRU处理cache数据块的读*/
void search(struct Group* group,long long vis,long long E,int flag2){
int ok=0;
int full=1;
int pid=0;
/*找cache中是否存在*/
for(long long i=0;i<E;i++){
if(group->lines[i].valid==1&&vis==group->lines[i].s_add) {
ok=1;
pid=i;
group->lines[i].LRU_counter=0;
}
if(group->lines[i].valid==0) full=0;
}
if(ok){
if(output) printf("hit ");
hit_count++;
for(long long i=0;i<E;i++){
if(i==pid) continue;
group->lines[i].LRU_counter++;
}
return;
}
else{
if(output) printf("miss ");
miss_count++;
}
if(full){ /*当前满*/
if(output) printf("eviction ");
eviction_count++;
long long mx=0;
long long id=0;
/*找到要踢出的块*/
for(long long i=0;i<E;i++){
if(mx<group->lines[i].LRU_counter){
mx=group->lines[i].LRU_counter;
id=i;
}
}
group->lines[id].valid=1;
group->lines[id].s_add=vis;
group->lines[id].LRU_counter=0;
/*更新其他块*/
for(long long i=0;i<E;i++){
if(i==id) continue;
group->lines[i].LRU_counter++;
}
}
else{
/*新增加的块的dfn=0*/
int flag=1;
for(long long i=0;i<E;i++){
if(flag&&group->lines[i].valid==0){
group->lines[i].valid=1;
group->lines[i].s_add=vis;
group->lines[i].LRU_counter=0;
flag=0;
}
else if(group->lines[i].valid==1){
group->lines[i].LRU_counter++;
}
}
}
if(output&&flag2) printf("\n");
}
void solve(FILE* fp,struct Cache cache){
unsigned long address;
int siz;
/*读取文件*/
long long S=1<<cache.s;
char oper;
while( (fscanf(fp,"%c %lx,%d",&oper,&address,&siz) )!=-1 ){
if(oper=='I') continue;
long long ad=(address>>cache.b)&(S-1);/*该数据块的组索引*/
long long vis=(address>>cache.b)>>(cache.s);/*该数据块的标记位*/
if(oper=='S'||oper=='L'){
if(output){
printf("%c %lx %d",oper,address,siz);
}
search(&cache.groups[ad],vis,cache.E,0);/*cache中找块*/
}
if(oper=='M'){
if(output){
printf("%c %lx %d",oper,address,siz);
}
search(&cache.groups[ad],vis,cache.E,0);
search(&cache.groups[ad],vis,cache.E,1);
}
}
}
int main(int argc,char **argv)
{
long long s,E,b;
output=0;
FILE* fp=NULL;
char opt;
while( (opt = getopt(argc,argv,"hvs:E:b:t:") ) !=-1){
switch(opt){
case 'h':
printf("Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n");
printf("Options:\n");
printf(" -h Print this help message.\n");
printf(" -v Optional verbose flag.\n");
printf(" -s <num> Number of set index bits.\n");
printf(" -E <num> Number of lines per set.\n");
printf(" -b <num> Number of block offset bits.\n");
printf(" -t <file> Trace file.\n");
printf("Examples:\n");
printf(" linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n");
printf(" linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n");
exit(EXIT_SUCCESS);
case 'v':
output=1;/*是否输出*/
break;
case 's':
s=atoll(optarg);
break;
case 'E':
E=atoll(optarg);
break;
case 'b':
b=atoll(optarg);
break;
case 't':
fp=fopen((const char*)optarg,"r");
if(fp==NULL){
printf("Open file wrong");
exit(EXIT_FAILURE);
}
break;
default:
exit(EXIT_FAILURE);
}
}
struct Cache cache=initCache(s,E,b);
solve(fp,cache);
printSummary(hit_count, miss_count, eviction_count);
release(cache);
return 0;
}
?PartB
挺魔鬼的..感觉没有彻底吃透
图片参考:https://www.bilibili.com/read/cv2955433/
首先做这个题,我们需要两张图,方便思考。
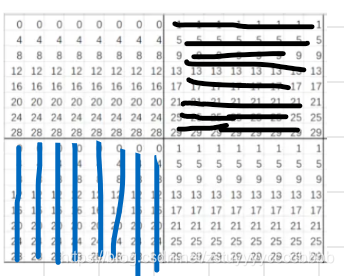
cache的s=5,E=1,b=5.
因此这是32X32时候每个int对应到cache中的组索引?

因此这是64X64时候的组索引?。
?
?先来考虑32X32.
我们发现,一次读掉一行,然后进行转置,如此进行第一个8X8之后。此时cache【0】存A【0】【0】~A【0】【7】。
再进行处理的时候,此时cache【0】,cache【8】,cache【16】...cache【28】已经存下来了。我们想让命中尽可能多,此时可以尝试把第一个8X8的矩阵完成转置。
但是你看到当cache【0】被B覆盖的时候,A【0】【0】~A【0】【7】此时就只赋值了一个,剩下的抖动掉了。
于是我们尝试用12个变量中的8个,来保存这次的A【0】【0】~A【0】【7】,这样就不用再去读导致miss了。
因此我们采取8个一块的策略。
可以观察到,除了对角线上存在多一点的抖动,其他地方主要一次冷不命中。
其结果命中图如下:


?可以计算出A的miss总数为32*4=128
B的miss总数为32*4+7*4=156.
总共为284。
测验得287.说明有函数开销。
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
if(M==32&&N==32){
for (int i = 0; i < N; i +=8 )
{
for (int j = 0; j < M; j +=8 ){
for(int k=0;k<8;k++){
int temp_value0 = A[i+k][j];
int temp_value1 = A[i+k][j+1];
int temp_value2 = A[i+k][j+2];
int temp_value3 = A[i+k][j+3];
int temp_value4 = A[i+k][j+4];
int temp_value5 = A[i+k][j+5];
int temp_value6 = A[i+k][j+6];
int temp_value7 = A[i+k][j+7];
B[j][i+k] = temp_value0;
B[j+1][i+k] = temp_value1;
B[j+2][i+k] = temp_value2;
B[j+3][i+k] = temp_value3;
B[j+4][i+k] = temp_value4;
B[j+5][i+k] = temp_value5;
B[j+6][i+k] = temp_value6;
B[j+7][i+k] = temp_value7;
}
}
}
}?输入./test-trans -M 32?-N 32 测验得287
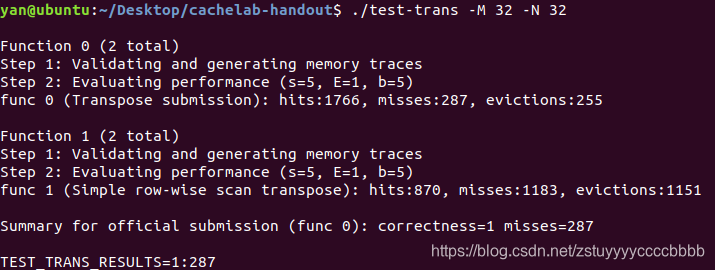
64X64的情况

?我们发现这次4行就是一轮回了,沿用上次代码发现miss率非常高。模拟一下第一个8x8的块就发现存在反复抖动的现象。
我们尝试4X4的分块,发现将刚才的代码改成4X4,能到1699次。其实还是可以的。但是不够优秀。因为我们没有充分利用每次的cache块里面的后面空间。
这里想了挺久不会,参考了网上的题解。
图片来源:https://blog.csdn.net/weixin_43821874/article/details/86481338
? 尝试一个折中的办法,就是将8*8和4*4相结合。虽然不能直接移动到目的,我们可以缓存在一个地方,再放进去。
具体如下:
首先将红色块移至目的地,再将黄色块移至红色块左边“暂存”一下。此时移动是伴随着转置的。
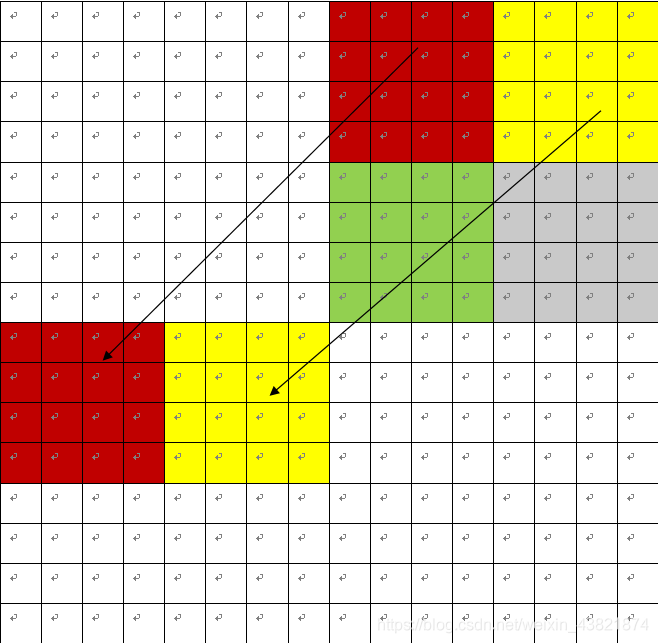
?再实现图中的移动即可,将黄色块移到红色块的下面,在将绿色快移到之前“暂存”黄色块的地方,最后将灰色块移动到目的地即可。
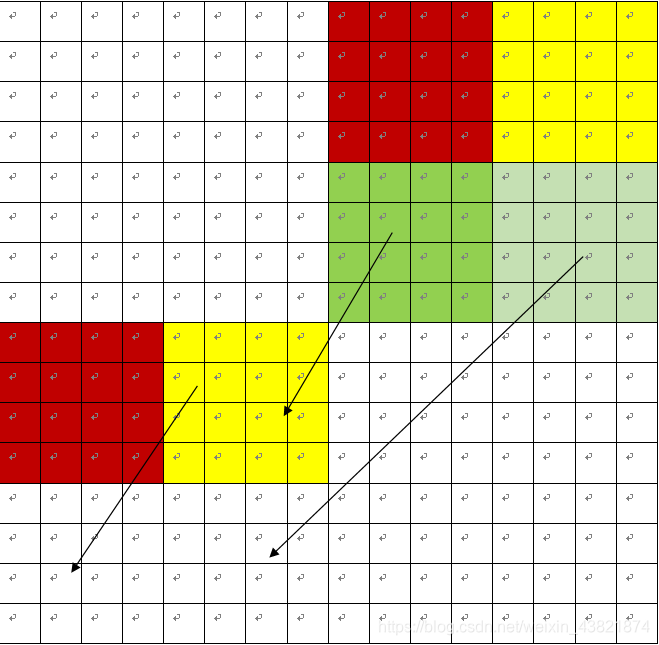
?模拟这个过程还有一个很重要的细节问题。

?结合这张图就能发现。
“再实现图中的移动即可,将黄色块移到红色块的下面,在将绿色快移到之前“暂存”黄色块的地方,最后将灰色块移动到目的地即可。”过程中,我们移动黄色(上一次已经转置)的时候是横着一次性移动过来的,而不是竖着对应竖着。因为横着一次就能把此时的cache【0】用完不用再取黄色块了。而如果竖着每次回来还要接着抖动更多的次数。
因此由黄色块横着移过去,所以绿色块移动方式也确定下来了。用竖着的一列来填补cache[0]。
这样一来就节省很多了。
最后再把灰色的横着转置过来就行,灰色部分提前一步已经在cache中了,黄块转移好的时候cache[0],[8],[16],[24]也好了。因此命中率杠杠的。
if(M==64&&N==64){
for(int i=0;i<N;i+=8){
for(int j=0;j<M;j+=8){
for(int k=i;k<i+4;k++){
int t0=A[k][j];
int t1=A[k][j+1];
int t2=A[k][j+2];
int t3=A[k][j+3];
int t4=A[k][j+4];
int t5=A[k][j+5];
int t6=A[k][j+6];
int t7=A[k][j+7];
B[j][k]=t0;
B[j+1][k]=t1;
B[j+2][k]=t2;
B[j+3][k]=t3;
B[j][k+4]=t4;
B[j+1][k+4]=t5;
B[j+2][k+4]=t6;
B[j+3][k+4]=t7;
}
for(int k=j;k<j+4;k++){
int t0=A[i+4][k];
int t1=A[i+5][k];
int t2=A[i+6][k];
int t3=A[i+7][k];
int t4=B[k][i+4];
int t5=B[k][i+5];
int t6=B[k][i+6];
int t7=B[k][i+7];
B[k][i+4]=t0;
B[k][i+5]=t1;
B[k][i+6]=t2;
B[k][i+7]=t3;
B[k+4][i]=t4;
B[k+4][i+1]=t5;
B[k+4][i+2]=t6;
B[k+4][i+3]=t7;
}
for(int k=i;k<i+4;k++){
int t1=A[k+4][j+4];
int t2=A[k+4][j+5];
int t3=A[k+4][j+6];
int t4=A[k+4][j+7];
B[j+4][k+4]=t1;
B[j+5][k+4]=t2;
B[j+6][k+4]=t3;
B[j+7][k+4]=t4;
}
}
}
}?61X67不能被完整地分块。网上的思路是暴力多次实验块的大小,测得17X17的无脑方式是够的。
因此我们按照17X17的方式分块。
看来不能完整分块的时候还是要多暴力尝试各种分块方式。
if(N==67&&M==61){
for(int i=0;i<N;i+=17){
for(int j=0;j<M;j+=17){
for(int k=i;k<i+17&&k<N;k++){
for(int p=j;p<j+17&&p<M;p++){
int temp=A[k][p];
B[p][k]=temp;
}
}
}
}
}
结语
这个lab还是比较折磨人的。partA部分只是个开胃小菜,让你手动来一个cache。对于LRU的策略优化的时间复杂度还可以优化。不过这是算法部分的策略了,不是这个lab的目的。
partB部分是感觉比较难,难在考虑的情况不好考虑,具体的不命中策略不好计算,当然可以用自己做的partA部分和后期拿到的数据来找哪里的不命中来分析。但是感觉过于细节。难度还是在于不命中率的整体思考角度和想法。
同时其中的转移模拟可以手动模拟,如果容易晕并且麻烦可以代码输出路径,这样更方便模拟,更好找路径以及发现时候存在漏移错移。
起码知道几点:
1.能整块分的尽量按照整块的大小去分。
2.不能整块的暴力尝试分块大小优化。
3.直接转移的命中率高,可以尝试间接转移,找到“缓存区”来转移
4.wsl2很坑
以及对cache有了进一步的理解。