题意:求二叉树的凸包面积
分析:任意方法推出公式即可
参考代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int k;
scanf("%d",&k);
double xrr,yrr,xl,yl,xr,yr;
scanf("%lf%lf%lf%lf%lf%lf",&xrr,&yrr,&xl,&yl,&xr,&yr);
double X=xr-xl;
double H=abs(yrr-yr);
double S3=H*X/2.0;
double l=2*(k-2)+1/pow(2,k-2);
l=l*2-1-2+1/pow(2,k-2);
l*=X;
double T=l*H/2;
double ans=T+S3;
printf("%.3lf\n",ans);
}
}题面:Link with Balls?
题意:m个球,先取0~n个球,再用n个可以取任意个球的框取完剩下的球,求方案数。
分析:枚举先取几个球,再用插板法得到选取方案?隔板法详解(各种方法),于是答案为: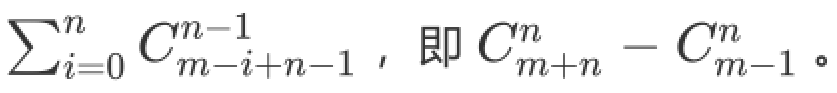
最后套个组合数的板子就好了。
参考代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod=1e9+7;
const int N=3e6;//记得开大
ll fac[N],inv[N];
ll ksm(ll a,ll b,ll p)
{
a%=p;
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
void init()
{
fac[0]=1;
for(int i=1;i<=N;i++)
fac[i]=fac[i-1]*i%mod;
inv[N]=ksm(fac[N],mod-2,mod);
for(int i=N-1;i>=0;i--)
inv[i]=inv[i+1]*(i+1)%mod;
}
int C(int n,int m){
if(m>n) return 0;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{
init();
int t;
cin>>t;
while(t--)
{
int n,m;
cin>>n>>m;
cout<<(C(m+n,n)-C(m-1,n)+mod)%mod<<endl;
}
}题面:Link with EQ
题意:给你条长为n的板凳,每个人都会尽可能选择高情商的坐法,求板凳期望坐下的人数。
分析:先算长度为x时两端有人期望坐下的人数f(x),再算长度为x时一端有人期望坐下的人数g(x),因为是高情商坐法,实际上在任意一端有人时都只有一种坐法(离最近的人最远),故递推可得对f(x)与g(x)当x确定时函数值也唯一确定。最后设h(x)为长度为x的板凳期望坐下的人数(坐哪都相当于两个一端有人的g(x)),且第一个人的坐法是等概率的,故最后对g(x)算个前缀和,每次直接查询期望就好了。



参考代码:
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int N=2e6;
#define ll long long
int f[N],g[N],sum[N],h[N];
void init()
{
for(int i=3;i<=N/2;i++)
{
int tmp=ceil((i-1)/2);
f[i]=(f[tmp]+f[(i-1)-tmp]+1)%mod;//两端有人中间坐
}
for(int i=2;i<=N/2;i++)
{
g[i]=(f[i-1]+1)%mod;//一端有人远了坐
sum[i]=(sum[i-1]+g[i])%mod;
}
}
ll ksm(ll a,ll b,ll p)
{
a%=p;
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
int main()
{
init();
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
printf("%d\n",(1+2*sum[n-1]*ksm(n,mod-2,mod))%mod);
}
}题意:某人卡在了空中,并且他开始往随机方向以初速度为v扔手榴弹(手榴弹受重力g=10影响),经过t秒后手榴弹爆炸,爆炸范围为r,求某人的生存几率(答案作为分数对1e9+7取模)。
分析:考虑转换参考系,给人和手榴弹都加一个反向重力,于是人往上做匀加速直线运动,手榴弹往v方向做匀速直线运动,易求得人和手榴弹最后的位置,于是两球半径和球心距都已知,问题转化为两球相切表面积问题。不会戳这里?球缺体积和球冠表面积的计算公式及应用,算出来的球冠表面积可由余弦定理算出的cosθ表示为2π(vt)^2(1-cosθ),球的表面积公式为4π(vt)^2,故死亡率为(1-cosθ)/2,生存率为(1+cosθ)/2。
?

参考代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod=1e9+7;
const int g=10;
int read()
{
int x=0;char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) x=x*10+c-'0',c=getchar();
return x;
}
void write(int X)
{
if(X<0) {X=~(X-1); putchar('-');}
if(X>9) write(X/10);
putchar(X%10+'0');
}
ll ksm(ll a,ll b,ll p)
{
a%=p;
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
int main()
{
int t;
cin>>t;
while(t--)
{
__int128 t,v,r;//由于我总是担心爆ll
t=read(),v=read(),r=read();
if(4*v*g*t*t*t+4*v*v*t*t+g*g*t*t*t*t-4*r*r<=0) cout<<0<<endl;//必死
else if(4*v*g*t*t*t+4*v*v*t*t+g*g*t*t*t*t-4*r*r>=8*v*g*t*t*t) cout<<1<<endl;//必活
else write((4*v*g*t*t*t+4*v*v*t*t+g*g*t*t*t*t-4*r*r)*ksm(8*v*g*t*t*t,mod-2,mod)%mod),cout<<endl;
}
}题意:求所有环的点权平均值是否相等。
分析:跑了dfs超时(为什么我的dfs跑不出),还是用拓扑吧。跑两次,第一次跑不成环的,将所有成环的点的入度减到1,再对所有环跑一次求平均值即可(自环也算环)。
参考代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int a[100005],ind[100005];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
memset(ind,0,sizeof ind);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),ind[a[i]]++;
queue<int>q;
for(int i=1;i<=n;i++) if(ind[i]==0) q.push(i);
while(!q.empty())
{
int u=q.front();
int v=a[u];
q.pop();
ind[v]--;
if(ind[v]==0) q.push(v);
}
ll ssum=0,scnt=0,f=0;
for(int i=1;i<=n;i++)
{
ll sum=0,cnt=0;
if(ind[i]==0) continue;
while(ind[i])
{
sum+=i;
cnt++;
ind[i]--;
i=a[i];
}
if(ssum==0)
{
ssum=sum;
scnt=cnt;
}
else if(ssum*cnt!=sum*scnt) f=1;
}
if(f) printf("NO\n");
else printf("YES\n");
}
}题意:贪吃蛇吃食物,每次只出现一个食物且前后两个食物不在同一行同一列,输出用最短时间吃到食物的操作序列(c顺时针,u逆时针,f前进)。
分析:直接模拟即可
参考代码:
#include<bits/stdc++.h>
using namespace std;
int X[100005],Y[100005];
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//上右下左
int n;
int zhuanx1(int x,int y,int to,int now)//0 0 0 1
{
int tx=X[now]-x;
int ty=Y[now]-y;
if(tx>0) tx=1;
else tx=-1;
if(ty>0) ty=1;
else ty=-1;
if(dir[to][0]!=tx&&dir[to][1]!=ty)
{
if(dir[(to+1)%4][0]==tx)
{
to=(to+1)%4;
cout<<"c";
}
else if(dir[(to+1)%4][1]==ty)
{
to=(to+1)%4;
cout<<"c";
}
else if(dir[(to-1+4)%4][0]==tx)
{
to=(to-1+4)%4;
cout<<"u";
}
else if(dir[(to-1+4)%4][1]==ty)
{
to=(to-1+4)%4;
cout<<"u";
}
}
return to;
}
int zhuanx2(int x,int y,int to,int now)//0 0 0 1
{
int tx=X[now]-x;
int ty=Y[now]-y;
if(tx>0) tx=1;
else if(tx<0) tx=-1;
if(ty>0) ty=1;
else if(ty<0) ty=-1;
if(dir[(to+1)%4][0]==tx&&dir[(to+1)%4][1]==ty)
{
to=(to+1)%4;
cout<<"c";
}
else if(dir[(to-1+4)%4][0]==tx&&dir[(to-1+4)%4][1]==ty)
{
to=(to-1+4)%4;
cout<<"u";
}
return to;
}
void tcs(int x,int y,int to,int now)//当前坐标 方向 第几次
{
if(now>n)
{
cout<<endl;
return;
}
to=zhuanx1(x,y,to,now);//第一次转向
while(x!=X[now]&&y!=Y[now])//一种方向走完
{
x+=dir[to][0];
y+=dir[to][1];
cout<<"f";
}
if(x!=X[now])//走另一种
{
to=zhuanx2(x,y,to,now);//第二次转向
while(x!=X[now])
{
x+=dir[to][0];
y+=dir[to][1];
cout<<"f";
}
}
else if(y!=Y[now])
{
to=zhuanx2(x,y,to,now);//第二次转向
while(y!=Y[now])
{
x+=dir[to][0];
y+=dir[to][1];
cout<<"f";
}
}
tcs(x,y,to,now+1);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int x,y,to;
scanf("%d%d%d",&x,&y,&to);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&X[i],&Y[i]);
}
tcs(x,y,to,1);
}
}题意:比较喝的速度p与倒的速度q。
分析:签到
参考代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
double p,q;
cin>>p>>q;
if(p>q) cout<<"ENJ0Y YOURS3LF!"<<endl;
else cout<<"N0 M0R3 BL4CK 1CE TEA!"<<endl;
}
}