【c++复健】算法啊,深度优先和dfs广度优先算法bfs
这几天摸了下深度优先算法和广度优先算法。
这俩本质思想是一样的,只不过每次搜的下一个节点不同。
深度优先算法是优先知道一个树中某一个分支的最远的值。优先判断有无子节点,如果有就继续递归,如果无就考虑父节点的其他子节点。
而广度优先算法是一层层的遍历,优先考虑兄弟节点,如果没有,就考虑子节点。
直接上算法题。

这道题没规定是否需要新建树,所以我就直接原地替换了。
官方答案点开我蒙了,反正我没看懂他在干嘛【】
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 != nullptr && root2 != nullptr){
root1->val += root2->val;
if(root1->left != nullptr && root2->left != nullptr){
mergeTrees(root1->left,root2->left);
}
else if(root1->left == nullptr && root2->left != nullptr){
root1->left = root2->left;
}
if(root1->right != nullptr && root2->right != nullptr){
mergeTrees(root1->right,root2->right);
}
else if(root1->right == nullptr && root2->right != nullptr){
root1->right = root2->right;
}
}
else if(root1 == nullptr && root2 != nullptr){
root1 = root2;
}
else if(root1 != nullptr && root2 == nullptr){
root1 = root1;
}
else{
return 0;
}
return root1;
}
};
执行用时: 40 ms , 在所有 C++ 提交中击败了
66.45% 的用户 内存消耗:
31.5 MB , 在所有 C++ 提交中击败了
81.93% 的用户

这个题他实际上还是树,只不过他根节点最多有四个子节点,最少有2个子节点。
其余节点的子节点在两个到三个之间,不过这不重要。
本质上还是一样的,只不过要写四种方向的判断,判断是否是一整个色块。
哦对了,这个题实际上就是刷漆桶问题,题目描述太过混乱。。。。。
直接上代码,这个题更重要的反而是这个vector的定义方法hh,整了好半天,背下来算了。
class Solution {
public:
int s1=-1;
int s2=-1;
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
s1=sr;
s2=sc;
vector<vector<bool>> visit(image.size(),vector<bool>(image[0].size(),false));
dfs(image,sr,sc,newColor,visit);
image[sr][sc]=newColor;
return image;
}
void dfs(vector<vector<int>>& image, int sr, int sc, int newColor,vector<vector<bool>>& visit){
visit[sr][sc]=true;
int v[][2]={{-1,0},{1,0},{0,1},{0,-1}};
for(int i=0;i<4;i++){
int x=sr+v[i][0];
int y=sc+v[i][1];
if(x>=0&&x<image.size()&&y>=0&&y<image[0].size()&&image[x][y]==image[s1][s2]&&!visit[x][y]){
image[x][y]=newColor;
dfs(image,x,y,newColor,visit);
}
}
}
};
下一题和刷漆桶问题类似,他是计算岛屿面积,然后找出最大的那一个。
实际上也是刷漆桶,但是这个不需要改变颜色(但是实际操作中我还是把岛屿的val改成了水的val,这样就可以遍历找岛),而是统计大小。
那区别就在于,需要遍历整个图找到每一个岛屿,然后计算他的面积大小,然后保存在一个temp里面,再去找下一个岛,然后将面积和temp比较,取大的。
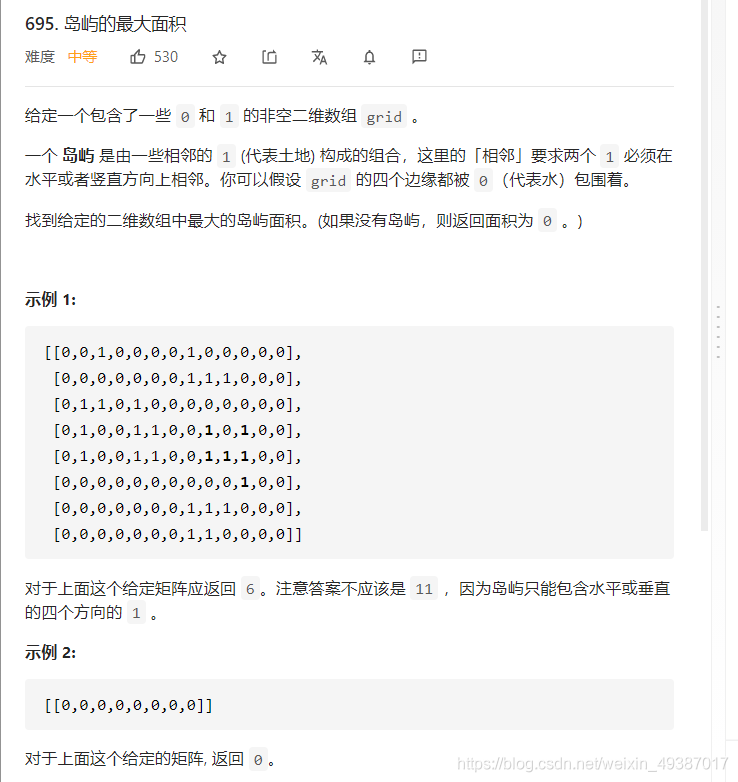
直击上代码,没什么好记录的。
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int lsr = grid.size();
int lsc = grid[0].size();
vector<vector<bool>> visit(grid.size(),vector<bool>(grid[0].size(),false));
int result = 0;
for(int i = 0;i<lsr;i++){
for(int j = 0;j<lsc;j++){
if(grid[i][j] != 0){
int re = 1;
re = isAIsland(grid,i,j,visit,re);
if(result < re){
result = re;
}
}
}
}
return result;
}
int isAIsland(vector<vector<int>>& grid, int sr, int sc, vector<vector<bool>>& visit, int temp){
visit[sr][sc] = true;
int v[][2] = {{-1,0},{1,0},{0,1},{0,-1}};
for(int i = 0;i<4;i++){
int x=sr+v[i][0];
int y=sc+v[i][1];
if(x>=0&&x<grid.size()&&y>=0&&y<grid[0].size()&&grid[x][y]!= 0&&!visit[x][y]){
grid[x][y] = 0;
temp = isAIsland(grid,x,y,visit,temp);
temp++;
}
}
return temp;
}
};
再来个递归题目,:

大意就是把二叉树里面的同层的节点用next连起来,最右边的节点next是空。
我用递归的做的,只需要考虑子节点中,左节点连右节点,右节点连自己的next节点的左节点。
要判读next节点不为空,如果为空的话。
父节点的next节点不为空,则子节点的右节点的next不为空。
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if(root == NULL){
return root;
}
else if(root->left == NULL){
return root;
}
root->left->next = root->right;
if(root->next){
root->right->next = root->next->left;
}
connect(root->left);
connect(root->right);
return root;
}
};
顺便记录一下官方解法,这个是遍历算法。
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr) {
return root;
}
// 初始化队列同时将第一层节点加入队列中,即根节点
queue<Node*> Q;
Q.push(root);
// 外层的 while 循环迭代的是层数
while (!Q.empty()) {
// 记录当前队列大小
int size = Q.size();
// 遍历这一层的所有节点
for(int i = 0; i < size; i++) {
// 从队首取出元素
Node* node = Q.front();
Q.pop();
// 连接
if (i < size - 1) {
node->next = Q.front();
}
// 拓展下一层节点
if (node->left != nullptr) {
Q.push(node->left);
}
if (node->right != nullptr) {
Q.push(node->right);
}
}
}
// 返回根节点
return root;
}
};