跳跃表是啥,跳跃表我个人理解就是多层级的链表,第0级的拥有全部节点,层级往上节点的个数越少,在工程实践上,可以作为红黑树的替代品,redis的有序集合的底层也是基于跳跃表实现的,可以快速的实现查找操作。本质上我认为是一种空间换取时间复杂度的数据结构。
首先来看跳跃表章啥样:
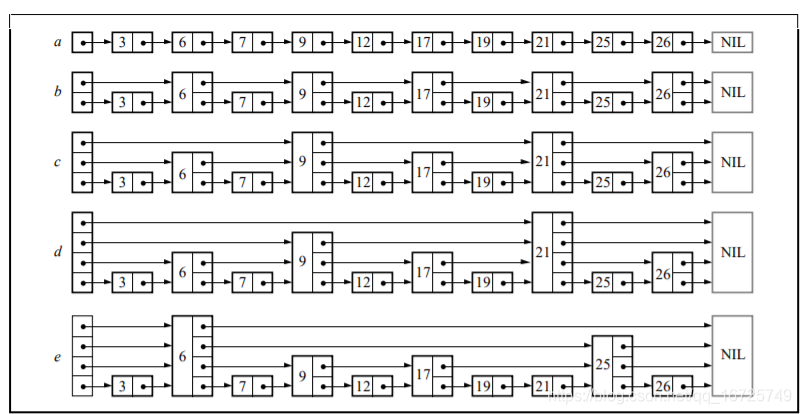
?其实跳跃表的节点里面有一个key,但是它有一个指针数组,每一层级的指针连接起来就是一个单链表。层级越低,节点数越多,低层级不出现的节点,也不会出现在高层级。最左边有个头节点,初始化的时候,用户输入跳跃表最高层级和概率,如果概率是0.5的话,假设0级有16个节点,1级就有8个,2级就有4个,以此类推。
插入:

现在要插入17,首先要初始化更新点数组update[maxlvl],?从上层开始找,找到各层中最后小于17的节点的指针。查找是可以加速的,每次向下移动,不需要从header开始找更新点,比如说,第三层小于17的数字是6,第二层寻找更新点的时候,可以从6这个节点作为开始。
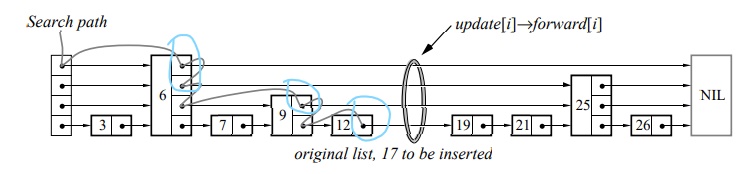
?更新点保存的指针我用蓝线圈起来了。
然后找到最后一个更新点的下一个节点,也是指向19的指针。也就是说17确实是不存在的,17如果存在的话,就没要插入了。接下来就是构造要插入的节点应该要在哪几层出现,如果说被构造的指针要在很高的层上面出现,这个高度甚至高于现在最高的节点。那么从level + 1 到 rlevel(待插入的节点的层数)层的节点要特殊处理。0到level层的节点其实就是多个单链表的插入。rlevel是通过概率产生的,rlevel越大,产生的概率越低。插入17后,17是一定要出现在0层的,有0.5的概率出现在1层,有0.25的概率出现在2层。
删除:

现在要删除17,?要找到各级的更新点,方法和插入函数寻找更新点的方法是一样的。此时找到current是指向12的指针,然后current = current->forward[0],是指向节点17的指针,对比值,确实这个节点就是要删除的节点。然后就是单链表的删除了,从0层向上删除,好处就是轮到第二层做删除17的操作的时候,发现第二层压根没有17这个节点,删除到此结束,第二层不存在的节点,第三层也绝对不会存在。接着要更新跳跃表的level。
查找:

?查找我认为是体现跳跃表高效的地方,假设。要查找19,首先从第三层的header查起,先查到6,然后从第二层的6继续查找,然后从第一层的6开始查找,然后查到9。然后从第一层的9开始查起,查到12。然后比较12的下一个节点是否就是19,如果是,就找到,如果不是,就没找到。
复杂度:
跳跃表查找,删除,插入的平均复杂度是O(logN),空间复杂度是O(N)。优秀的查找,删除,插入速度以及并不很大的时间复杂度使得跳跃表这种数据结构得到了广发的使用。
代码:
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
class Node{
? ? public:
? ? ? ? int key;
? ? ? ? Node ** forward;//多级链表,就是一个指针数组
? ? ? ? Node(int,int);
};
Node::Node(int key,int level){
? ? this->key = key;
? ? forward = new Node*[level + 1];
? ? memset(forward,0,sizeof(Node*) * (level + 1));
}
class SkipList{
? ? int maxlvl;//最高层数
? ? float p;//概率值
? ? int level;//当前最高的节点的层数
? ? Node* header;//头节点
public:
? ? SkipList(int,float);
? ? int randomlevel();//插入的时候返回随机层数
? ? Node* creatNode(int,int);
? ? void insertElem(int);
? ? void deleteElem(int);
? ? void searchElem(int);
? ? void displayList();
};
SkipList::SkipList(int maxlvl,float p){
? ? this->maxlvl = maxlvl;
? ? this->p = p;
? ? level = 0;//初始化层数
? ? header = new Node(-1,maxlvl);
}
int SkipList::randomlevel(){
? ? //返回一个随机层数,层数越高,到达的概率越低
? ? float r =(float)rand() / RAND_MAX;//0 - 1
? ? int lvl = 0;
? ? while(r < p && lvl < maxlvl){
? ? ? ? lvl++;
? ? ? ? r = (float)rand() / RAND_MAX;
? ? }
? ? return lvl;
? ? //假设我们设置的概率是0.5,那么可以到1层的概率是0.5
}
Node* SkipList::creatNode(int key,int level){
? ? Node* n = new Node(key,level);
? ? return n;
}
void SkipList::insertElem(int key){
? ? Node* current = header;
? ? Node* update[maxlvl + 1];//更新点,其实跳跃表就是多级的链表
? ? memset(update,0,sizeof(Node*) * (maxlvl + 1));//全部初始化为空指针
? ? for(int i = level;i >= 0;i--){//level是当前最高的节点的层数,找插入点要从最高的层开始找
? ? ? ? while(current->forward[i] != NULL && current->forward[i]->key < key){
? ? ? ? ? ? current = current->forward[i];
? ? ? ? }
? ? ? ? update[i] = current;//每一层的更新点,保存
? ? }
? ? current = current->forward[0];//最低一层的更新点的下一个节点
? ? if(current == NULL || current->key != key){
? ? ? ? int rlevel = randomlevel();
? ? ? ? if(rlevel > level){//生成的随机层数大于当前存在的level的话
? ? ? ? ? ? for(int i = level + 1;i < rlevel + 1;i++){
? ? ? ? ? ? ? ? update[i] = header;//也就是说如果要插入的节点的层数很高,甚至高过当前的level,高过当前的level的
? ? ? ? ? ? ? ? //更新点用header来赋值
? ? ? ? ? ? }
? ? ? ? ? ? level = rlevel;//更新最高节点的层数
? ? ? ? }
? ? ? ? Node* n = creatNode(key,level);//生成要插入的节点
? ? ? ? for(int i = 0;i <= rlevel;i++){
? ? ? ? ? ? n->forward[i] = update[i]->forward[i];
? ? ? ? ? ? update[i]->forward[i] = n;//其实就是多级单链表的插入罢了,从第0级开始插入
? ? ? ? }
? ? ? ? cout<<"插入节点成功 "<<key<<"\n";
? ? }
}
void SkipList::searchElem(int key){
? ? Node* current = header;
? ? for(int i = level;i >= 0;--i){
? ? ? ? while(current->forward[i] && current->forward[i]->key < key){
? ? ? ? ? ? current = current->forward[i];//查找是从最高层开始查找的,然后转移到下一层继续查找
? ? ? ? ? ? //通过多级索引的方式减少时间复杂度,本质上是空间换时间的做法
? ? ? ? }
? ? }
? ? current = current->forward[0];
? ? if(current && current->key == key){
? ? ? ? cout<<"找到了key:"<<key<<"\n";
? ? }
? ? else{
? ? ? ? cout<<"找不到key: "<<key<<"\n";
? ? }
}
void SkipList::deleteElem(int key){
? ? Node* current = header;
? ? Node* update[maxlvl + 1];
? ? memset(update,0,sizeof(Node*) * (maxlvl + 1));
? ? for(int i = level;i >= 0; i--){
? ? ? ? while(current->forward[i] != NULL && current->forward[i]->key < key){
? ? ? ? ? ? current = current->forward[i];//从上往下找
? ? ? ? }
? ? ? ? update[i] = current;//找更新点,其实就是要删除的节点的前一列指针都要找到
? ? }
? ? current = current->forward[0];//
? ? if(current != NULL && current->key == key){//如果确实current就是要被干掉的节点
? ? ? ? for(int i = 0;i <= level;i++){
? ? ? ? ? ? //删除要从下往上删除,级别越低的链表都不存在的节点,不会在高级别的链表上存在
? ? ? ? ? ? if(update[i]->forward[i] != current)
? ? ? ? ? ? ? ? break;//用不着再往上进行删除了
? ? ? ? ? ? update[i]->forward[i] = current->forward[i];//多级链表的删除
? ? ? ? }
? ? }
? ? delete current;
? ? while(level > 0 && header->forward[level] == NULL){
? ? ? ? level--;//更新跳表的层数
? ? }
? ? cout<<"删除节点:"<<key<<"\n";
}
void SkipList::displayList(){
? ? ?cout<<"\n skiplist"<<"\n";
? ? ?for(int i = 0; i < level;i++){
? ? ? ? Node* node = header->forward[i];
? ? ? ? cout<<"level"<<i<<":";
? ? ? ? while(node){
? ? ? ? ? ? cout<<node->key<<" ";
? ? ? ? ? ? node = node->forward[i];
? ? ? ? }
? ? ? ? cout<<"\n";
? ? ?}
}
int main()
{
? ? srand((unsigned)time(0));
? ? SkipList l(3,0.5);
? ? l.insertElem(3);
? ? l.insertElem(6);
? ? l.insertElem(7);
? ? l.insertElem(9);
? ? l.insertElem(12);
? ? l.insertElem(19);
? ? l.insertElem(17);
? ? l.insertElem(26);
? ? l.insertElem(21);
? ? l.insertElem(28);
? ? l.insertElem(23);
? ? l.insertElem(11);
? ? l.insertElem(1);
? ? l.displayList();
? ? l.deleteElem(19);
? ? l.displayList();
? ? l.searchElem(6);
? ? l.searchElem(600);
? ? return 0;
}