[数据结构与算法]《剑指offer》JZ1 ~ JZ10

JZ1:二维数组中的查找

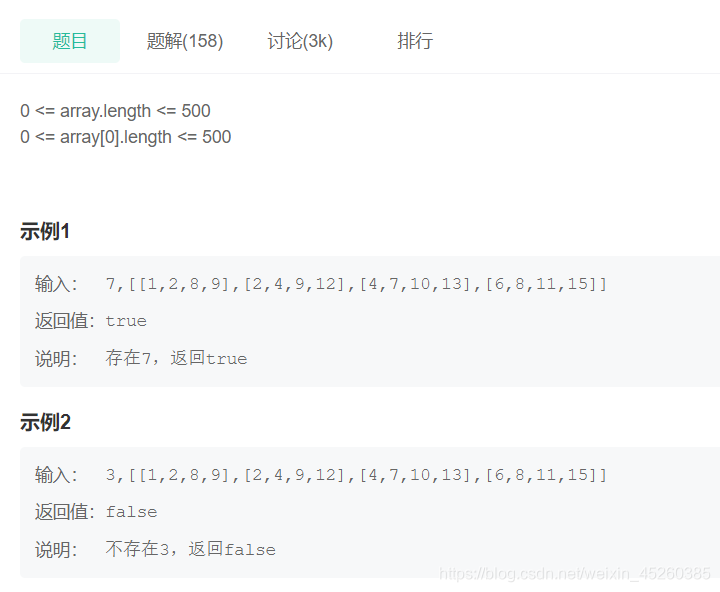
每个一维数组都用二分找.
看了题解还有直接二维数组二分的…

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
        for(int i=0;i<array.size();i++)
        {
            if(array[i].size()==0) continue;
            if(array[i][0] > target) break;
            
            int l=0,r=array[i].size()-1;
            while(l<=r)
            {
                int mid = l+(r-l)/2;
                if(array[i][mid]>target) r=mid-1;
                else if(array[i][mid]<target) l=mid+1;
                else return true;
            }
            
        }
        return false;
    }
};

JZ2:替换空格

过于简单,不宜展示…

JZ3:从尾到头打印链表

先反转链表,再跑一遍取到每个值,纯属为了多写一遍反转链表的代码

关于原地反转链表的博客 (注意有无头节点)

可以直接遍历一遍链表,然后将值放入vector,最后reverse

class Solution {
public:
    vector<int> printListFromTailToHead(ListNode* head) {
        vector<int> ans;
        if(head==NULL) return ans;
        // 反转链表
        ListNode* p = head;
        ListNode* q = NULL;
        ListNode* t;
        while(p)
        {
            t = p->next;
            p->next = q;
            q = p;
            p = t;
        }
        
        while(q)
        {
            ans.push_back(q->val);
            q = q->next;
        }
        return ans;
    }
};

JZ4:重建二叉树

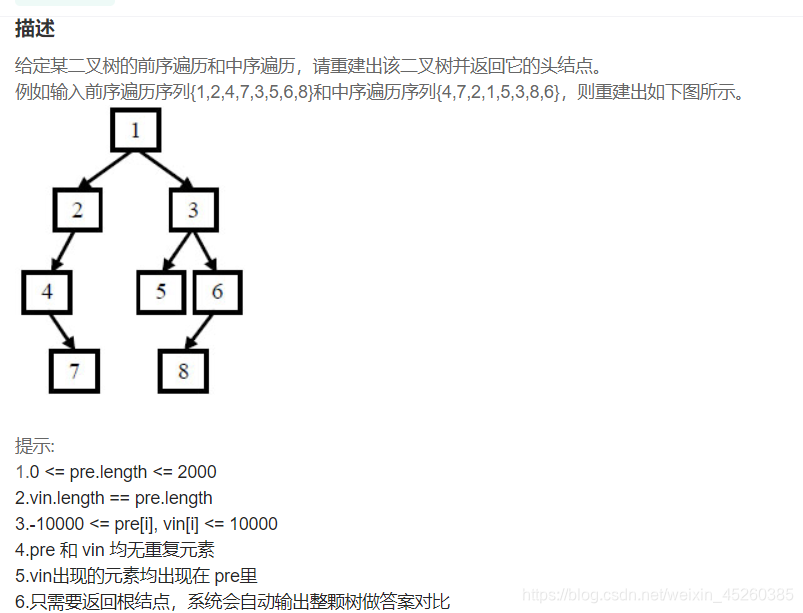
经典的建树,以前写的博客就很多,静态的也有…

类似1

类似2

class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        return create(0, pre.size()-1, 0, vin.size()-1, pre, vin);
    }
    
    TreeNode* create(int qz,int qy,int zz,int zy,vector<int> pre,vector<int> vin)
    {
        if(qz>qy) return NULL;
        TreeNode* root = new TreeNode(pre[qz]);
        int k=zz;
        for(;k<=zy;k++)
            if(vin[k] == pre[qz]) break;
        
        int num = k-zz;
        root->left = create(qz+1,qz+num,zz,k-1,pre,vin);
        root->right= create(qz+1+num,qy,k+1,zy,pre,vin);
        return root;
    }
};

JZ5:用两个栈实现队列

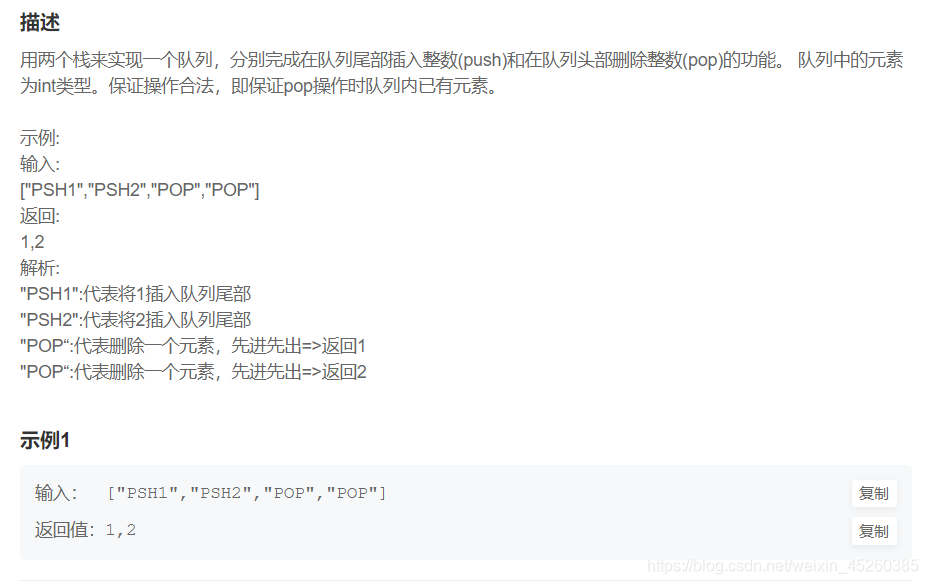
栈的特点是先进后出,队列是先进先出

先用stack1存入push的值,然后再存入stack2,那么倒了两次也就正了,第二个栈也就实现了先进先出…此后,出队都用stack2,而入队都用stack1,等stack2空了(不空就存入会影响顺序),再把stack1存进stack2.

class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        if(stack2.size()==0)
        {
            while(stack1.size())
            {
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        
        int p = stack2.top();
        stack2.pop();

        return p;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

JZ6:旋转数组的最小数字

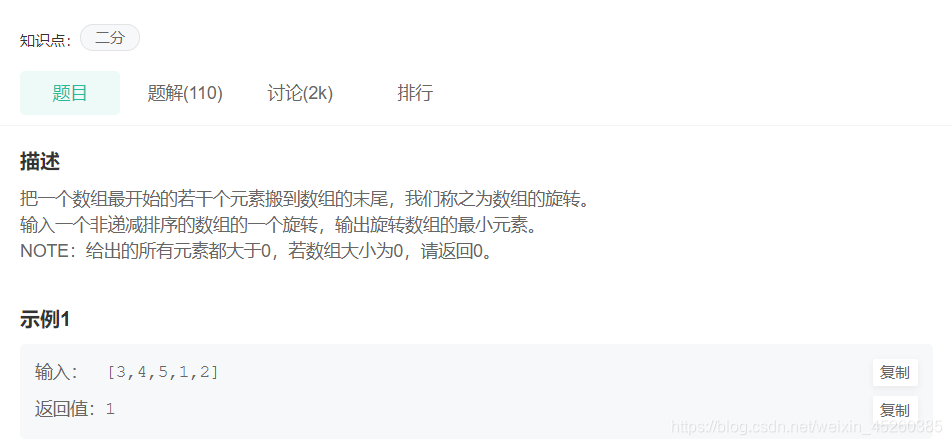
特点: ① 数组非递减 ② 把一个数组最开始的若干个元素搬到数组的末尾

此处选择右端点进行比较:
① mid大于右端点:由于原本数组非递减,所以最小值一定在mid右边
② mid小于右端点:最小值为mid或mid左侧
③ mid等于右端点:无法确定最小值,因此不断左移右端点.

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        int l=0,r=rotateArray.size()-1;
        while(l<r)
        {
            int mid=l+(r-l)/2;
            if(rotateArray[mid]>rotateArray[r])  l=mid+1;
            else if(rotateArray[mid]<rotateArray[r]) r=mid;
            else r--;
        }
        return rotateArray[l];
    }
};

JZ7:斐波那契数列

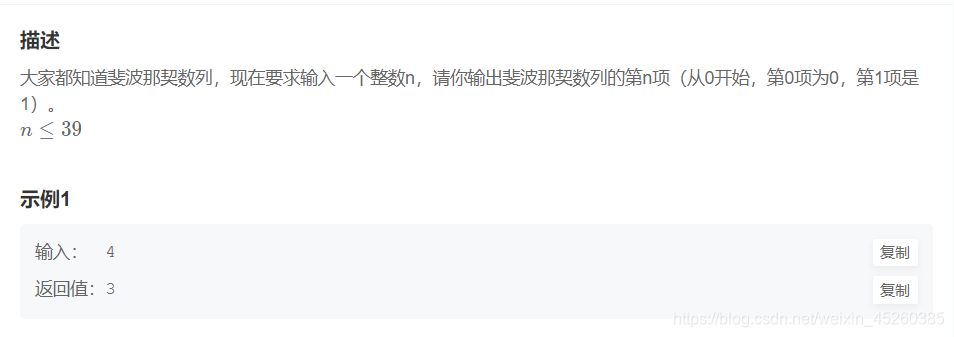
过于简单,不宜展示…

JZ8:跳台阶

此类题目思路就是,当前层的上一步的所有跳法之和
例如需要到第4层,且一次只能跳1或2层
那么就计算第3层和第2层的跳法之和即可,因为这两层可以一步到第4层

因为刚好是只能跳1或2层,所以代码和经典斐波那契差不多

class Solution {
public:
    int jumpFloor(int number) {
        if(number<=2) return number;
        int a=1,b=2,c;
        for(int i=3;i<=number;i++)
        {
            c=a+b;
            a=b;
            b=c;
        }
        return c;
    }
};

JZ9:跳台阶扩展问题

找到了规律,如果找不到规律,根据题意, 每一层的跳法就是前面所有层的跳法加起来再+1(直接跳到该层) 即可

class Solution {
public:
    int jumpFloorII(int number) {
        if(number<=2) return number;
        return pow(2.0,number-1);
   }
};

JZ10:矩形覆盖

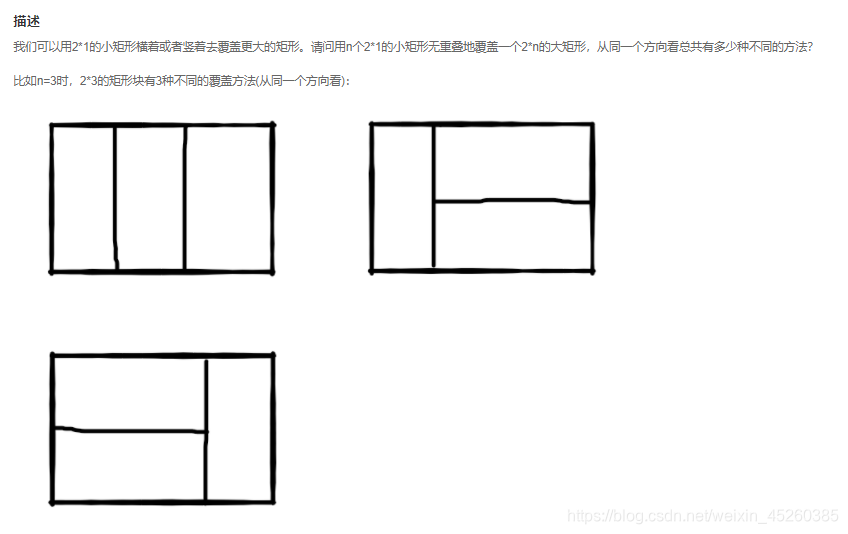
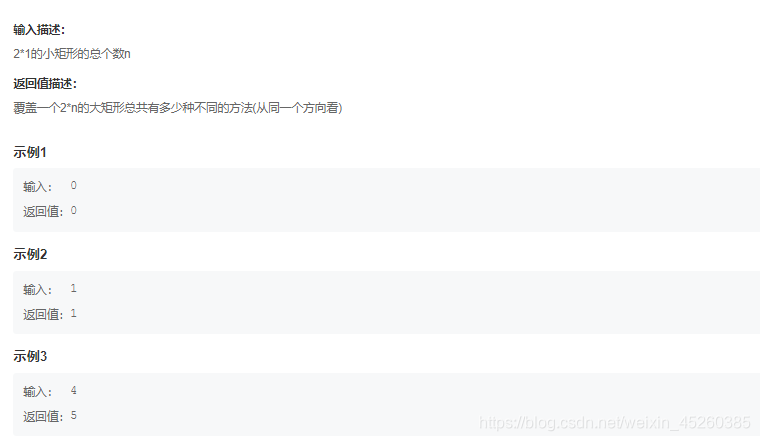
这种类型的题八九不离十就是找规律(JZ7~JZ10代码都差不多),写几个出来就看得出来规律了

class Solution {
public:
    int rectCover(int number) {
        int a=1,b=2,c;
        if(number<2) return number;
        for(int i=3;i<=number;i++)
        {
            c=a+b;
            a=b;
            b=c;
        }
        return c;
    }
};