[数据结构与算法]数据结构与算法

数据结构与算法

2.算法分析

2.1算法的时间复杂度分析

事后分析估算法

public static void main(String[] args) {
    long start =System.currentTimeMillis();

    int sum=0;
    int n=100;
    for (int  i= 1; i<= n; i++) {
        sum += i;

    }
    System.out.println("sum=" +sum);

    long end=System.currentTimeMillis();
    System.out.println(end-start);
}

事前分析估算方法

程序在计算机上运行所消耗的时间主要取决于该算法的运行时间和问题输入规模

需求：计算1到100的求和

解法一：算法时间复杂度o(n)

public static void main(String[] args) {
    int sum=0;  //执行一次
    int n=100;  //执行一次
    for (int i = 1; i < n; i++) {   //执行了n=1次
        sum +=i;  //执行n次
    }
    System.out.println("sum=" +sum);
}

解法二：算法时间复杂度o(1)

public static void main(String[] args) {
    int sum=0;  //执行一次
    int n=100;  //执行一次
    sum=(n+1)*n/2;  //执行一次
    System.out.println("sum=" +sum);
}

2.2算法函数规则

1.算法函数中的常数可以忽略；

2.算法函数中最高次幂的常数因子可以忽略；

3.算法函数中最高次幂越小，算法效率越高。

2.3算法时间复杂度

2.3.1大o记法

推导大o表示法的规则：

1.用常数1取代运行时间的所有加法常数；

2.在修改后的运行次数中，只保留高阶项；

3.如果最高阶项存在，且常数因子不为1，则去除最高项的常数；

2.3.2常见的大o阶

1.线性阶o(n)

一般含有非嵌套循环设计线性阶，线性阶就是随着输入规模的扩大，对应计算次数呈直线增长。

下面这段代码，它的循环时间复杂度为O(n),因为循环体中的代码需要执行n次

public static void main(String[] args) {
    int sum = 0;  //执行一次
    int n = 100;  //执行一次
    for (int i = 1; i <= n; i++) {
        sum += i;
    }
    System.out.println("sum= " + sum);
}

2.平方阶o(n^2)

一般含有嵌套循环

下面这段代码含有嵌套循环，所以时间复杂度为o(n^2)

int sum = 0;  
int n = 100;  
for (int i = 1; i <= n; i++) {
    for (int j = 0; j <= n; j++) {
        sum+=i;
    }
}
System.out.println("sum= " + sum);

3.立方阶o(n^3)

一般含有三层嵌套循环

下面这段代码，每个嵌套执行100次，三个则是100^3次，则时间复杂度为立方阶

 public static void main(String[] args) {
        int x=1;
        int n=100;
        for (int i = 1; i <=n; i++) {  
            for ( int j = i; j < n; j++) {
                for ( j = i ; j <= n; j++) {
                    x++;
                }
            }
        }
        System.out.println(x);

    }
}

4.对数阶o(log n)

下面这段代码，可以看出结果为2^x,当结果大于n时，则退出循环，由高中对数知识，可知x=log(2)n,故时间复杂度为o(log n)

public static void main(String[] args) {
    int i=1,n=100;
    while (i<n){
        i =i*2;
    }
}

5.常数阶0(1)

一般不涉及循环操作的都是常数阶，因为不会随着n的增长而增加操作次数。

以下的代码不管n为多少，都只执行2次，故时间复杂度为o(1)。

public static void main(String[] args) {
    int  n = 100;
    int sum=n*(n+1)/2;
    System.out.println(sum);
}

对常见时间复杂度总结：

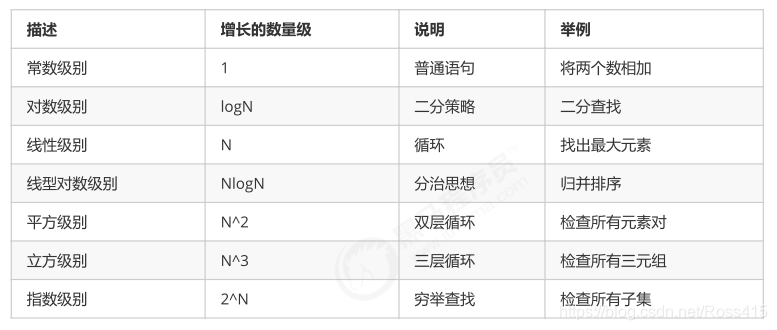
时间复杂度排序：o(1)<o(log n)<o(n)<o(n log n)<o(n^2)<o(n3)

我们尽量在设计结构时，尽量追求的是o(1)，o(log n)，o(n)，o(n log n)这几种时间复杂度，其他的则是不可取，需要进行优化。

2.3.3函数调用的时间复杂度分析

案例一：

下面代码包含一个for循环，而show方法只执行了一行代码，所以show方法的时间复杂度为o(1),而main函数的时间复杂度为o(n).

public static void main(String[] args) {
    int  n = 100;
    for (int i = 0; i < n; i++) {  
        show(i);
    }

}
private static void show(int i){
    System.out.println(i);
}

案例二：

在main函数中有一个for循环，再加上循环体调用了show方法，而show方法包含一个循环，故main方法的时间复杂度为o(n^2)

public static void main(String[] args) {
    int  n = 100;
    for (int i = 0; i < n; i++) {
        show(i);
    }

}
private static void show(int i){
    for (int j = 0; j < i; j++) {
        System.out.println(i);
    }

案例三：

show方法有一个for循环，而main方法在for循环中调用了，另外一个for循环中嵌套了一个循环，故时间复杂度为o(n^2)

public static void main(String[] args) {
    int  n = 100;
    show(n);
    for (int i = 0; i < n; i++) {
        show(i);
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            System.out.println(j);
        }
    }

}
private static void show(int i){
    for (int j = 0; j < i; j++) {
        System.out.println(i);
    }
}

2.3.4最坏情况

案例：在一个存储了n个随机数字的数组里，找出指定的数字

public int search(int num) {
    int[] arr = {11, 10, 8, 9, 7, 22, 23, 0};
    for (int i = 0; i < arr.length; i++) {
        if (c == arr[i]) {
            return i;
        }
    }
    return -1;

最好情况：查找第一个数字就是期望的数字，则算法的时间复杂度为o(1);

最坏情况;

查找的最后一个数字为期望的数字时，算法的时间复杂度为o(n)

平均情况:

每个数字查找的平均复杂度为o(n/2)

最坏情况是一种最基本的保障，即使在最坏的情况下，也能够正常的提供服务。注：除非特殊说明，一般提到的运行时间都指的是最坏情况下的运行时间

2.4算法的空间复杂分析

算法的空间复杂度来描述对内存的占用

2.4.1Java中常见内存占用情况：

1.基本数据类型内存占用情况：

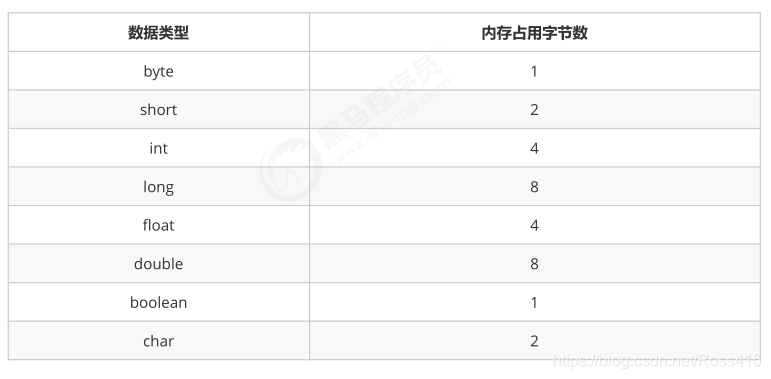
2.计算机访问内存的方式都是一次一个字节

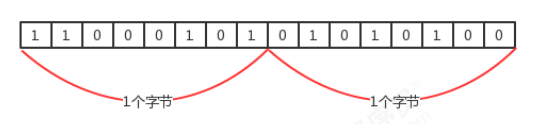
3.一个引用（机器地址）需要8个字节表示：

例如：Data data =new Date();则data这个变量需要占用8个字节来表示

4.创建一个对象，比如 new Data()，除了Data对象内部存储的数据占用的内存，该对象本身也需要占用内存，每个对象占用16个字节，用来保存对象的头信息。

5.一般内存的使用，如果不够8个字节，都会自动被填充为8字节

6.Java中数组被限定为对象，他们一般都会因为记录长度而需要额外的内存，一个原始类型的数组一般需要24字节的头信息，再加上保存值所需要的内存。

2.4.2算法的空间复杂度

了解Java的内存最基本的机制，能够有效帮助我们估计大量程序的内存使用情况。

算法的空间复杂度计算公式：S(n)=O(f(n))，其中n为输入规模，f(n)为语句关于n所占存储空间的函数。

Data对象内部存储的数据占用的内存，该对象本身也需要占用内存，每个对象占用16个字节，用来保存对象的头信息。

5.一般内存的使用，如果不够8个字节，都会自动被填充为8字节

6.Java中数组被限定为对象，他们一般都会因为记录长度而需要额外的内存，一个原始类型的数组一般需要24字节的头信息，再加上保存值所需要的内存。

2.4.2算法的空间复杂度

了解Java的内存最基本的机制，能够有效帮助我们估计大量程序的内存使用情况。

算法的空间复杂度计算公式：S(n)=O(f(n))，其中n为输入规模，f(n)为语句关于n所占存储空间的函数。

但现在电脑的内存比较大，所以不需要去考虑这些。所以普通情况下说复杂度指的是算法的时间复杂度。