[数据结构与算法]《梯度下降法》

概述

• 目的：对原始模型的损失函数进行优化，以便寻找到最优的参数，使得损失函数的值最小
• 梯度指向误差值增加最快的方向，导数为0（梯度为0向量）的点，是一个寻找最优点的过程
• 学习率：学习率或步长，控制迭代的快慢，太小会导致收敛很慢，太大导致会无法收敛
• 梯度下降法容易陷入局部最优解
• 一元线性回归只有全局最优解，没有局部最优解

推导

? 找到合适参数$\theta$，使得损失函数$J(\theta )$(连续可微)最小
$$J(\theta )$$
? 一阶泰勒展开，得到
$$J(\theta )\approx J({\theta }_0)+(\theta ?{\theta }_0)?J^{,}({\theta }_0)+\alpha$$

式中，α是误差项。

? 参数的每次调整
$$\theta ?{\theta }_0=\lambda v$$
? λ是变化大小（标量、步长、学习率）， v是变化方向。

? 每次调整参数，需要函数值减小，则
$$J(\theta )?J({\theta }_0)=\lambda v{J}^{,}({\theta }_0)<0$$
? 当梯度下降方向和微分方向完全相反时，速度下降最快
$$v?J^{,}({\theta }_{)}=||v||?||J^{,}({\theta }_0)||cos(\alpha )$$
? 当cos(α)<0，时向量乘积小于0 ，因为我们希望下降速度是最快的，所以令cos(α) = -1，即两个向量的方向相反
$$v=?\frac{J^{,}({\theta }_0)}{||J^{,}({\theta }_0)||}$$
? $$||J^{\prime }({\theta }_0)||$$为标量合并到λ中得到学习率$lr$，则参数的更新公式为
$$\theta ={\theta }_0?lr?J^{,}({\theta }_0)$$

应用

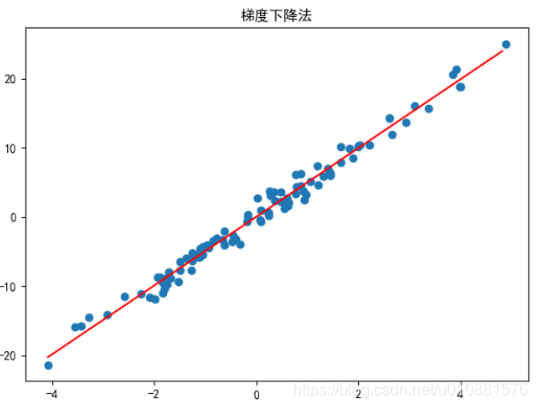
一元线性回归

• 仿真数据

m = 100
X = 2 * np.random.randn(m, 1)
Y = 5 * X +  np.random.randn(m, 1)

• 代价函数

def cost_function(theta, X, Y):
    return np.sum(theta[0] + theta[1] * X - Y) / (2*m)

• 梯度函数

def gradient_function(theta, X, Y):
    B = np.hstack([np.ones((m, 1)), X])
    diff = np.dot(B, theta) - Y
    return (1/m) * np.dot(B.transpose(), diff)

• 梯度下降

def gradient_descent(X, Y, alpha, iter_num = 1000):
    theta = np.ones((2, 1)) # 初始值
    J_ = gradient_function(theta, X, Y) # 求梯度
    num = 0
    while not all(abs(J_) <= 1e-5):     # 当梯度很小时，趋于平滑，最好是为0
        if num >= iter_num: # 限制迭代次数，防止一致不收敛
            break
        theta = theta - alpha * J_   # 梯度下降
        J_ = gradient_function(theta, X, Y)
        num += 1
    return theta

• 结果可视化

fig = plt.figure()
plt.scatter(X, Y)
X_ = np.arange(np.min(X), np.max(X), 0.1)
Y_ = theta[0] + theta[1] * X_
plt.plot(X_, Y_, color = 'red')
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.title('梯度下降法')
plt.show()

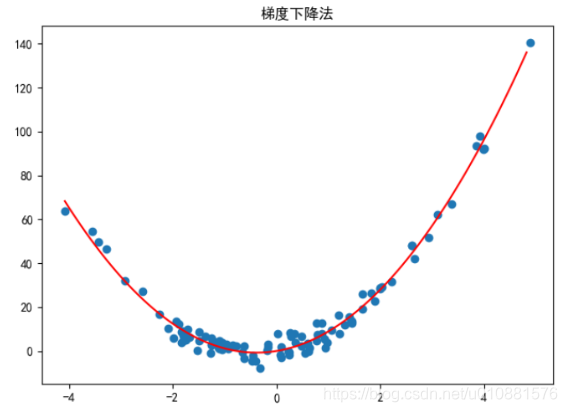
二元非线性回归

• 仿真数据

X = 2 * np.random.randn(m, 1)
Y = 5 * X **2  +  4 * X + 3 * np.random.randn(m, 1)

• 梯度下降

def  gradient_function(para, X, Y):
    B = np.hstack([X**2, X])
    diff = np.dot(B, para) - Y
    return (1/m) * np.dot(B.transpose(), diff)

• 可视化

求极值点

• 仿真函数

def fun(x, y):
    return 3 * x**2 + 4 * y**2

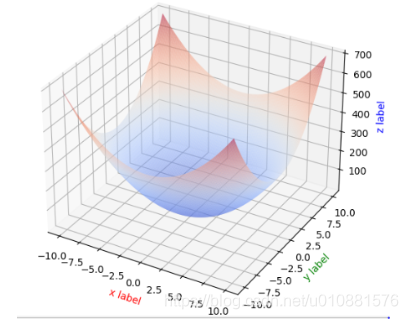
存在极小值

• 求极值点

def get_extreme_point():   # 极小值
    def gradient_func(x, y):
        return [6 * x , 8 * y]

    alpha = 0.01
    x0 = [100, 100]
    f0 = fun(x0[0], x0[1])

    for i in range(10000):
        print("[%d] (%.5f, %.5f): %.5f" % (i, x0[0], x0[1], f0))
        J = gradient_func(x0[0], x0[1])
        x1 = [x0[0]-alpha *J[0] ,x0[1] - alpha * J[1]]
        f1 = fun(x1[0], x1[1])
        if abs(f1 - f0) < 1e-9:
            print("极值点：", x0, " 极小值：", f0)
            break
        x0 = x1
        f0 = f1