算法篇

决策树

决策树的基本组成部分包括：根节点、分节点和叶子节点
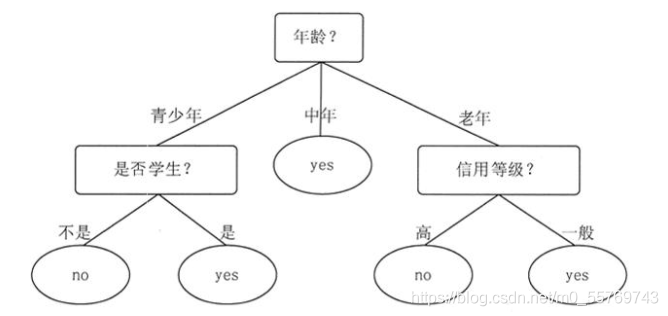
在这里插入图片描述
根节点和分节点通常用方块表示，叶子节点通常用椭圆表示。
决策树的关键在于怎样建立出这样的一个树，怎样建立出一个达到要求的前提下深度最小的树。决策树是由好几个算法组成的，每个算法都有不同的方法来解决构建树的问题。

决策树的优点

推理过程比较容易理解，决策推理过程可以表示为if-else的形式
推理过程完全取决于属性变量的取值特点
可以自动忽略对目标没有贡献的属性，能够判断属性的重要性

决策树中的算法

CLS、ID3、C4.5、CART四种，其中ID3、C4.5、CART都采用贪心方法，其中决策树以自顶向下递归的分治方法构造，并且大多数决策树算法都采用这种自顶向下的方法。所谓贪心方法，通俗的讲就是在选取根节点时把所有的都计算一遍，使用穷举的方法找到最优

**CLS算法

CLS是早期的决策树算法，它并没有给出怎样确定根节点，只是给出了创建决策树的具体方法，其他三种算法都是对CLS的延伸和优化，来看一下CLS算法的基本算法思想：

生成一棵空的决策树和一个训练集样本属性集
若训练集中所有样本都属于同一类，则生成叶子节点，终止算法
根据某种策略从训练集样本属性中选择属性作为分裂属性，生成测试节点
根据测试节点的取值不同分为不同的分支
从训练样本中删除已经分裂过的属性
转至步骤2重复操作，直到分裂出的所有都属于同一类停止
通俗点讲就是，随便选取一列作为根节点，如果它的所有取值都属于同一类就终止，否则删除该列，再根据删除列的取值分支在进行分裂，直到所有分裂都属于同一类。

**ID3算法

ID3算法主要针对的是属性选择问题，使用信息增益度来选择分裂属性

熵

首先就是要了解一下熵，熵是用来衡量信息量大小的，熵的计算要用到的加权平均信息量，先来看一下信息量的计算公式：
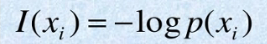
在这里插入图片描述
信息出现的概率越大，表示它的信息量越小，概率越小，信息量越大。比如当概率等于1时，信息量= - log(1)

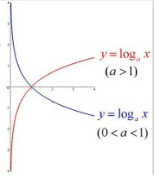
注意：在信息论中，对数通常是以2为底，所以在上图中只需要考虑红色的曲线即可
下面来介绍一下计算熵的公式：
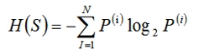
在这里插入图片描述
对于熵的理解可以简化为加权平均信息量。特征S有N种可能的取值，每一种可能出现的概率乘以它的信息量并相加就是加权平均信息量

条件熵

相当于条件概率

第一步先计算结果的熵值
再计算已知某个特征的情况下结果的熵值
比如：
某个特征里有三个取值，标签结果有两个取值
1、先计算出特征每个取值的概率，p1、p2、p3
2、计算每一个取值下结果的熵值
3、条件熵 = 三个取值下结果的三个熵值的加权平均

信息增益

信息增益的作用就是确定作为根节点的特征，用结果的熵值减去已知特征的情况下结果的条件熵，计算公式为：
Gain(特征) = H(结果) - H( 结果 | 特征 )
结论：选择信息增益最大的作为根节点

总结

先有一个若干特征一个标签的训练集
对标签计算出结果熵值
对所有特征中的取值计算对应结果的条件熵
计算每个特征的信息增益，选出最大值作为根节点
将分裂完成此列特征删除，如果结果为同一类，则终止算法
如果不是同一类，则继续计算剩下特征的信息增益，选取最大的作为下一次分裂的特征
重复计算信息增益，选择特征进行分裂，直至所有叶子节点为同一类结束

缺点

ID3只能处理特征为离散类型的数据，只能实现分类算法，假如编号也成为一个特征，编号算得的信息增益最大，则会优先选择编号作为根节点，但是我们并不希望让编号也算进特征中，ID3算法无法解决这种特别多属性值的数据，所以有了下面的C4.5算法来解决这一问题

**C4.5算法

在ID3的基础上做了一些优化，通过使用信息增益率选择分裂属性，克服了ID3算法中通过信息增益无法处理很多属性值的数据的缺陷，信息增益率能够处理离散数据和连续数据，还能处理有确实属性的训练数据。

信息增益率

信息增益率能够有效避免倾向于选择拥有多个属性值的样本
信息增益率公式：
Gainraio(特征) = Gain(特征) / H(特征)
选择增益率最大的特征作为根节点，使用流程和使用信息增益的流程一样

连续值处理

对于连续型数据的处理，就不能再使用信息增益率来处理了，下面来说一下连续值处理的步骤：

某一个特征中有N个连续型数据
将这一列数据去重后升序排序
求出相邻两个值的均值，这样就能得到N-1个数据
先使用第一个数据，计算小于第一个数据的值的条件熵，再计算出信息增益
依次计算剩下N-2个数据的信息增益
比较信息增益，选择最大的信息增益对应的属性值作为分裂点(比如有一列为密度的特征，当密度=0.318时信息增益是最大的，选择这个点为分裂点，这是它的取值就变成了小于0.318的和大于等于0.318的两类，再进行分裂)

结论

信息增益率可以处理属性值特别多的特征；离散数据在经过分裂后会被删除，但是经过连续值处理后的数据分裂后不会被删除，后续还能作为属性划分

缺点

通过上述处理，只能将连续特征进行二分处理，依然是只能实现分类算法，下面的算法又进行了改进，可以实现处理分类算法和回归算法

**CART算法

基尼值

基尼值代表了模型的不纯度，基尼值越小不纯度越低，特征越好。基尼值=样本被选中的概率 - 样本被分错的概率，用公式表示为
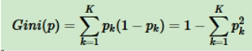
在这里插入图片描述
如果是二分类问题，基尼值还可以称为熵之半，公式可以写成：

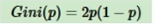
基尼值就相当于(信息量)熵，是对熵的优化，不用在使用log运算，使运算变得更加简单

基尼系数

基尼系数相当于信息增益，公式表示为：
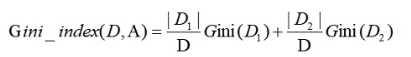
在这里插入图片描述
基尼系数针对的是二分类，只会分为是或否。对于某一个特征，特征里面的所有取值都要计算一下对应结果的基尼值，然后计算基尼系数，选取最小的作为分裂节点
基尼系数只能在分类算法中使用，在上面说过CART算法不仅可以用于分类算法，还能用于会在算法，那么用于回归算法就要使用下面的方法了。

平方误差

使用平方误差计算的是二分类回归算法，对连续型的标签进行处理，具体步骤为：

先选取某一特征的若干个取值进行计算，类似于条件熵，在已知取值的情况下结果的平均误差
选取平均误差小的作为分裂节点
再判断左节点如果小于等于3条，就终止左子树分裂；如果大于3条，就继续判断该节点的变换系数如果小于0.1就停止左子树分裂，否则继续分裂；右子树同理
删除分裂过的特征，继续判断剩下的特征哪个取值平均误差最小
直到变换系数小于0.1或行数小于3时停止，如果停止时标签仍然有两个以上的值，那么就取其均值作为结果
下面介绍一下平均误差的计算，因为是二分类，所以只分为是和否，分类为是的计算出平均误差加上分类为否的平均误差就是该节点平均误差。平均误差的公式为：( X - X均值 )**2，也可称为N次方差。
变换系数：也称为离散系数或者变化系数，离散系数等于标准差除以均值，但是在平均误差中使用的时平均误差除以均值

缺失值处理

在缺失值处理中使用最多的就是权重，下面以信息增益为例：

比如某一特征有缺失值，在计算该列的信息增益时要先把有缺失值的行去掉，计算剩下的行信息增益
其余特征有缺失值也是这样计算
通过对比计算出的信息增益，选择最大的作为根节点，但是这只是选择根节点的方法
选择出根节点后，根据取值进行分裂
比如根节点列有两个缺失值，分了三个分支，每个分支上的数据数目分别为7，5，3；这个时候要把缺失值加回来，因为缺失值对应的行还有结果信息，后续选择还需要使用，每个分支都要加上两个缺失值，三个分支上的数据就变成了9，7，5；
数据每一行的权重都是1，但是有缺失值就不一样了，由于每个分支上的无缺失数据有7，5，3；两个缺失值的权重就变成了：分支数据个数/(7+5+3+2)，也就是7/15，5/15，3/15，无缺值的权重还是1
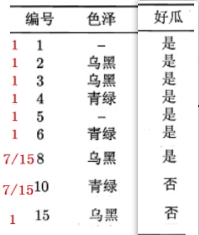
在根据权重分别计算剩余特征的信息增益，去除要计算特征的缺失值，首先计算结果的熵，H(结果) = -p1log(p1) - p2log(p2)，公式中的概率p需要根据权重来计算，p = 非缺失值权重 / 总权重，p1 = (4 + 7/15) / (5 + 2 * 7/15)，条件熵的计算同理，再选择信息增益最大的进行分裂，重复加权计算的过程