[数据结构与算法]力扣算法二叉树篇：树的深度

二叉树的深度

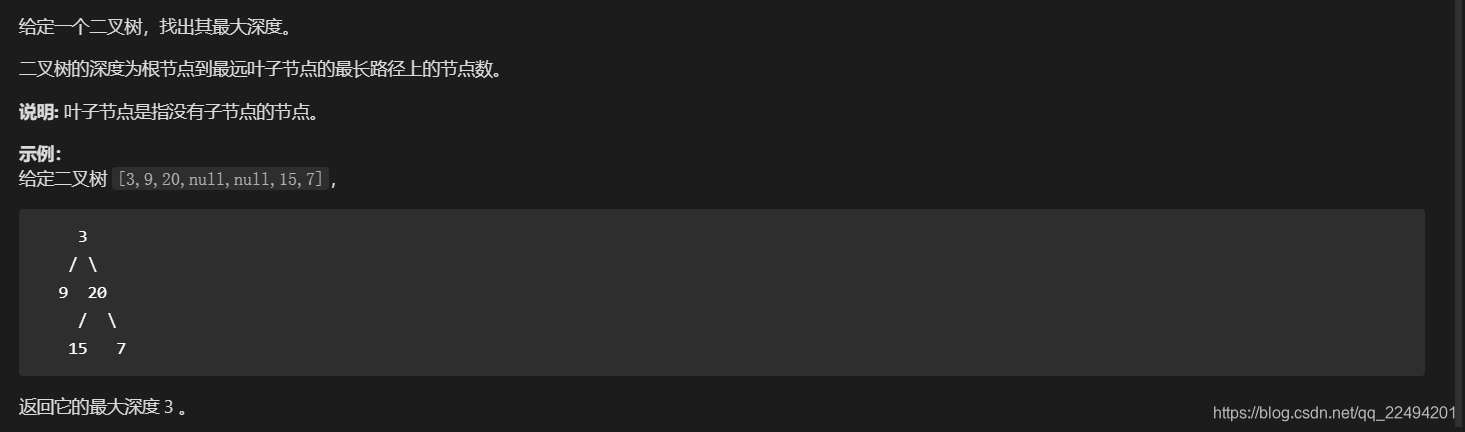
题解：

层序遍历计算深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        //为空直接返回0
        if(root == NULL){
            return 0;
        }
        //层序遍历 队列
        queue<TreeNode*> que;
        //根节点入队
        que.push(root);
        //二叉树的深度
        int deepth = 0;
        //遍历二叉树
        while(!que.empty()){
            //当层结点个数
            int size = que.size();
            //深度加1
            deepth++;
            for(int i =0;i<size;i++){
                //处理的当前结点
                TreeNode *cur = que.front();
                //弹出队头元素
                que.pop();
                //左右子树
                if(cur->left){
                    que.push(cur->left);
                }
                if(cur->right){
                    que.push(cur->right);
                }
            }
        }
        return deepth;
    }
};

递归：

前序遍历：深度回溯求深度

递归三部曲：
1、确定递归函数的参数和返回值
无返回值，参数为该结点的深度以及树结点
2、确定终止条件
没有左右子树（叶节点）时即可终止
3、确定单层递归逻辑
左右子树最深叶节点的深度的最大值

class Solution {
public:
    int result;
    //递归
    void getdepth(TreeNode * node,int depth){
        //中
        result = result>depth?result:depth;
        //左 左子树最深叶节点深度
        if(node->left){
            depth++;
            getdepth(node->left,depth);
            //回溯
            depth--;
        }
        //右子树最深叶节点深度
        if(node->right){
            depth++;
            getdepth(node->right,depth);
            //回溯
            depth--;
        }
        return;
    }
    int maxDepth(TreeNode* root) {
        //前序遍历
        //根节点为空 直接返回0
        if(root == NULL){
            return 0;
        }
        //否则 递归求深度
        getdepth(root,1);
        return result;
    }

};

后序遍历

递归三部曲：
1、确定递归函数的参数和返回值
参数为树的根节点，返回这棵树的深度
2、确定终止条件
空结点返回0
3、确定单层递归逻辑
求左子树深度，再求右子树深度，取左右子树深度的最大值再加1

class Solution {
public:
    //递归
    int getdepth(TreeNode * node){
       if(node==NULL){
           return 0;
       }
       //左子树深度
       int dep1 = getdepth(node->left);
       //右子树深度
       int dep2 = getdepth(node->right);
       //中
       int result = 1+max(dep1,dep2);
       return result;
    }
    int maxDepth(TreeNode* root) {
      //后序遍历 左右中
      int result = getdepth(root);
      return result;
    }
};

n叉树的深度

层序遍历

大致逻辑与求二叉树深度一致 代码整体即为n叉树的层序遍历逻辑

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        //为空直接返回0
        if(root == NULL){
            return 0;
        }
        //层序遍历 队列
        queue<Node*> que;
        //根节点入队
        que.push(root);
        //n叉树的深度
        int deepth = 0;
        //遍历二叉树
        while(!que.empty()){
            //当层结点个数
            int size = que.size();
            //深度加1
            deepth++;
            for(int i =0;i<size;i++){
                //处理的当前结点
                Node *cur = que.front();
                //弹出队头元素
                que.pop();
                //将结点的孩子结点加入队列
                for(int j = 0;j<cur->children.size();j++){
                    que.push(cur->children[j]);
                }
            }
        }
        return deepth;
    }
};

递归

递归三部曲：
1、确定递归函数的参数和返回值
参数为树的根节点，返回这棵树的深度
2、确定终止条件
空结点返回0
3、确定单层递归逻辑
求得孩子结点的最大深度，加1为树的深度

class Solution {
public:
    int maxDepth(Node* root) {
        //为空返回0
        if(root == NULL){
            return 0;
        }
        int depth = 0;
        //求得每一个孩子的深度
        for(int i = 0;i<root->children.size();i++){
            depth = max(depth,maxDepth(root->children[i]));
        }
        //树的深度为孩子结点最大深度+1
        return depth+1;
    }
};