[数据结构与算法] SMSC2021 Day9&Day10 部分题解

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> SMSC2021 Day9&Day10 部分题解 -> 正文阅读

[数据结构与算法]SMSC2021 Day9&Day10 部分题解

SMSC Day9&Day10

Day 9

T1 多边形 poly (简单数学)
T2 螃蟹 crab (期望，搜索，优先队列)

T3 三染色 tres (构造，二分图判定，动态规划解决判定性问题)

在这里插入图片描述
本题为构造题，可以考虑发掘一些性质，首先从题目给出的三个条件可以得到：

同色不与同色相邻，红色不与绿色相邻

由于红色与绿色的性质无差别，我们完全可以将它们看成一种颜色，暂且将它们看作白色。所以问题转化为给出一种染色方案使得这个图中的点同色不相邻，异色相邻。
先不考虑如何染色的问题，先考虑能否构造这种方案。我们可以通过 DFS 对图进行一次初步的染色，任意从一个点开始，用一种数字标记上它已经染色（不必在意是具体哪种颜色，因为现在正在判定而非构造），与它相邻的点用另一种数字标记表示与它颜色不同。每遍历到一个点都将相邻的未染色的点染上与它不同的颜色，并且对于相邻的染过色的点要判断是否合法，一旦遇到不合法的情况就证明不存在构造的方案。事实上，不合法的情况只有一种：图中有奇数个结点组成的环。
在判定可能可以构造一种方案后，我们考虑尝试构造一种合法的方案。对于不同的连通块，有一部分染蓝色，有一部分染白色，可能的情况如下：
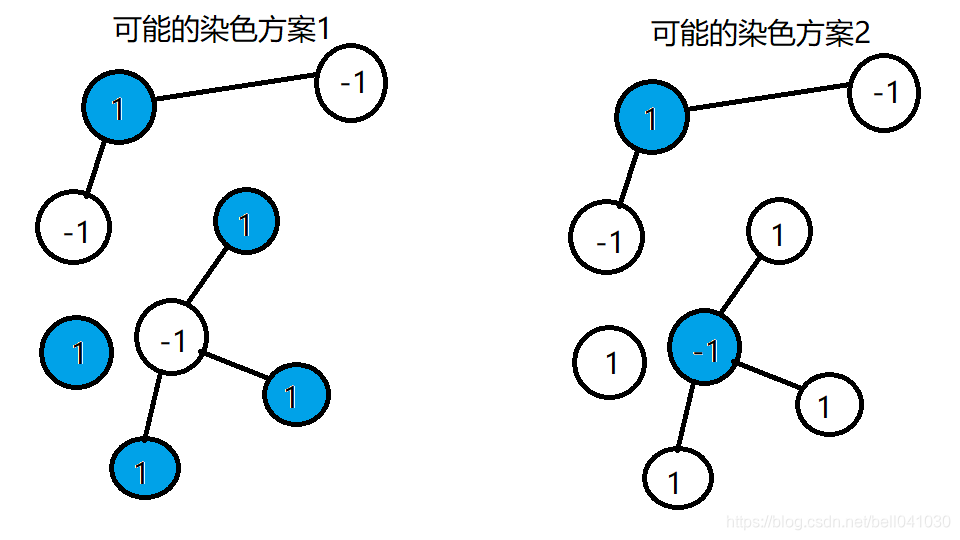
在这里插入图片描述

这其中 $1$ 和 $? 1$ 只是标记了点之间的相对颜色。
也就意味着我们要在 $k$ 个连通块中，给 $n_3$ 个点染上蓝色，或者给 $n_1+n_2$ 个点染上白色。为方便考虑，我们尝试解决在这 $k$ 个连通块中，给 $n_3$ 个点染上蓝色，而每个连通块中可选择的染色点数只有两种，这就转化为经典背包问题了，只不过目标是判定，不是最优化，问能否在这 $k$ 个连通块中选出刚好 $n_3$ 个点塞进背包里。
所以设 $f (i, j)$ 表示在前 $i$ 个连通块中能否塞进 $j$ 个蓝色点。所以有
$\text{if}\; f(i-1,j) = 1 ,f(i,j+siz_1(i)) = f(i,j+siz_2(i)) = 1$
同时为了记录构造的方案，我们要记录 DP 过程中的路径，然后我们就解决了这道题。时间复杂度 $O(nm+k^2)$ ， $k$ 表示连通块的个数。

#include<iostream>
#include<cstdio>

using namespace std;
int n,m,n1,n2,n3,tmp;
int x ,y,head[5005],cnter,siz[5005][2];
int cnt,col[5005],ans[5005],t[5005],v;
struct edge{
	int nxt;
	int to;
}e[12500005];

int pre[5005][5005],g[5005];
bool flag = 1,f[5005][5005],vis[5005];

void addedge(int from,int to)
{
	cnt ++;
	e[cnt].nxt = head[from];
	e[cnt].to = to;
	head[from] = cnt;
	cnt ++;
	e[cnt].nxt = head[to];
	e[cnt].to = from;
	head[to] = cnt;
	return ;
}

void dfs(int u)
{
	if(col[u] > 0) siz[cnter][1] ++;
	else siz[cnter][0] ++;
	t[u] = cnter;
	vis[u] = 1;
	for(int i = head[u];i;i = e[i].nxt)
	{
		v = e[i].to;
		if(!vis[v])
		{
			col[v] = -col[u];
			dfs(v);
		}
		else
		{
			if(col[u] == col[v])
			{
				flag = 0;
				return ;
			}
		}
	}
	return ;
}

int main()
{
	scanf("%d%d",&n,&m);
	scanf("%d%d%d",&n1,&n2,&n3);
	for(int i = 1;i <= m;i ++)
	{
		scanf("%d%d",&x,&y);
		addedge(x,y);
	}
	for(int i = 1;i <= n;i ++)
		if(!vis[i])
		{
			cnter ++;
			col[i] = 1;
			dfs(i);
		}
	if(flag == 0)
	{
		printf("-1\n");
		return 0;
	}
	f[0][0] = 1;
	for(int i = 1;i <= cnter;i ++)
	{
		for(int j = 0;j + siz[i][1] <= n3;j ++)
			if(f[i - 1][j] == 1)
			{
				f[i][j + siz[i][1]] = 1;
				pre[i][j + siz[i][1]] = j;
			}
		for(int j = 0;j + siz[i][0] <= n3;j ++)
			if(f[i - 1][j] == 1)
			{
				f[i][j + siz[i][0]] = 1;
				pre[i][j + siz[i][0]] = j;
			}
	}
	if(f[cnter][n3] == 0)
	{
		printf("-1");
		return 0;
	}
	tmp = n3;
	for(int i = cnter;i >= 1;i --)
	{
		g[i] = tmp - pre[i][tmp];
		tmp = pre[i][tmp];
	}
	for(int i = 1;i <= n;i ++)
	{
		if(g[t[i]] == siz[t[i]][1])
		{
			if(col[i] > 0)
			{
				ans[i] = 3;
				n3 --;
			}
			else
			{
				if(n1 > 0)
				{
					ans[i] = 1;
					n1 --;
				}
				else
				{
					ans[i] = 2;
					n2 --;
				}
			}
		}
		else
		{
			if(col[i] < 0)
			{
				ans[i] = 3;
				n3 --;
			}
			else
			{
				if(n1 > 0)
				{
					ans[i] = 1;
					n1 --;
				}
				else 
				{
					ans[i] = 2;
					n2 --;
				}
			}
		}
	}
	for(int i = 1;i <= n;i ++) printf("%d ",ans[i]);
	return 0;
}

T4 水 aqua (最小生成树，长链剖分)

Day 10

T1 矩阵 mat (构造，性质发掘)
T2 因数 div (数论，约数，质数，算术基本定理)CF1349A Orac and LCM

T3 中位数 mid (性质发掘)

CF1349B Orac and Medians
在这里插入图片描述

#include<iostream>
#include<cstdio>

using namespace std;
typedef long long ll;
ll T,n,k,a[500005];
bool flag, flag2;


int main()
{
	scanf("%lld",&T);
	for(int tt = 1;tt <= T;tt ++)
	{
		scanf("%lld%lld",&n,&k);
		flag2 = 0;
		for(int i = 1;i <= n;i ++)
		{
			scanf("%lld",&a[i]);
			if(a[i] == k) flag2 = 1;
		}
		flag = 0;
		if(flag2 == 0) 
		{
			printf("No\n");
			continue ;
		}
		if(n == 1)
		{
			printf("Yes\n");
			continue;
		}
		for(int i = 1;i < n;i ++)
			if(a[i] >= k && a[i + 1] >= k)
			{
				printf("Yes\n");flag = 1;
				break;
			}
		if(flag == 1) continue;
		for(int i = 1;i < n - 1;i ++)
			if(a[i] >= k && a[i + 2] >= k)
			{
				printf("Yes\n");flag = 1;
				break;
			}
		if(flag == 1) continue;
		printf("No\n");
	}
	return 0;
}

T4 接水果 nel (DP，数据结构优化 DP ，树状数组维护二维偏序)

在这里插入图片描述

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
typedef long long ll;
ll n,a[1000005],t[1000005];
ll f[1000005],ans,bit[1000005];
int map[1000005];

struct fru{
	ll tt;
	ll id;
}b[1000005];

ll GetMax(int i)
{
	ll res = 0;
	for(;i > 0;i -= (i&(-i))) res = max(res,bit[i]);
	return res; 
}

void Update(int i, ll x)
{
	for(;i <= n;i += (i&(-i))) bit[i] = max(bit[i],x);
	return ;
}

bool cmp(fru x,fru y)
{
	return x.tt < y.tt;
}

int main()
{
	scanf("%lld",&n);
	for(int i = 1;i <= n;i ++)
	{
		scanf("%lld",&t[i]);
		b[i].id = i;
		b[i].tt = i + t[i];
	}
	for(int i = 1;i <= n;i ++) scanf("%lld",&a[i]);
	sort(b + 1, b + 1 + n, cmp);
	int j = 1;
	for(int i = 1;i <= n;i ++)
	{ 
		f[i] = a[i]*t[i]; 
		for(;j <= n && b[j].tt <= i;j ++) Update(b[j].id,f[b[j].id]);//100pts
		f[i] = max(f[i],GetMax(i - t[i]) + a[i] * t[i]);
//		for(int j = 1;j < i;j ++)//40pts
//			if(j + t[j] <= i && i - t[i] >= j)
//				f[i] = max(f[i],f[j] + a[i]*t[i]);
	} 
	for(int i = 1;i <= n;i ++) ans = max(ans,f[i]);
	printf("%lld",ans);
	return 0;
}