[数据结构与算法]PTA甲级 1099 Build A Binary Search Tree (C++)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.

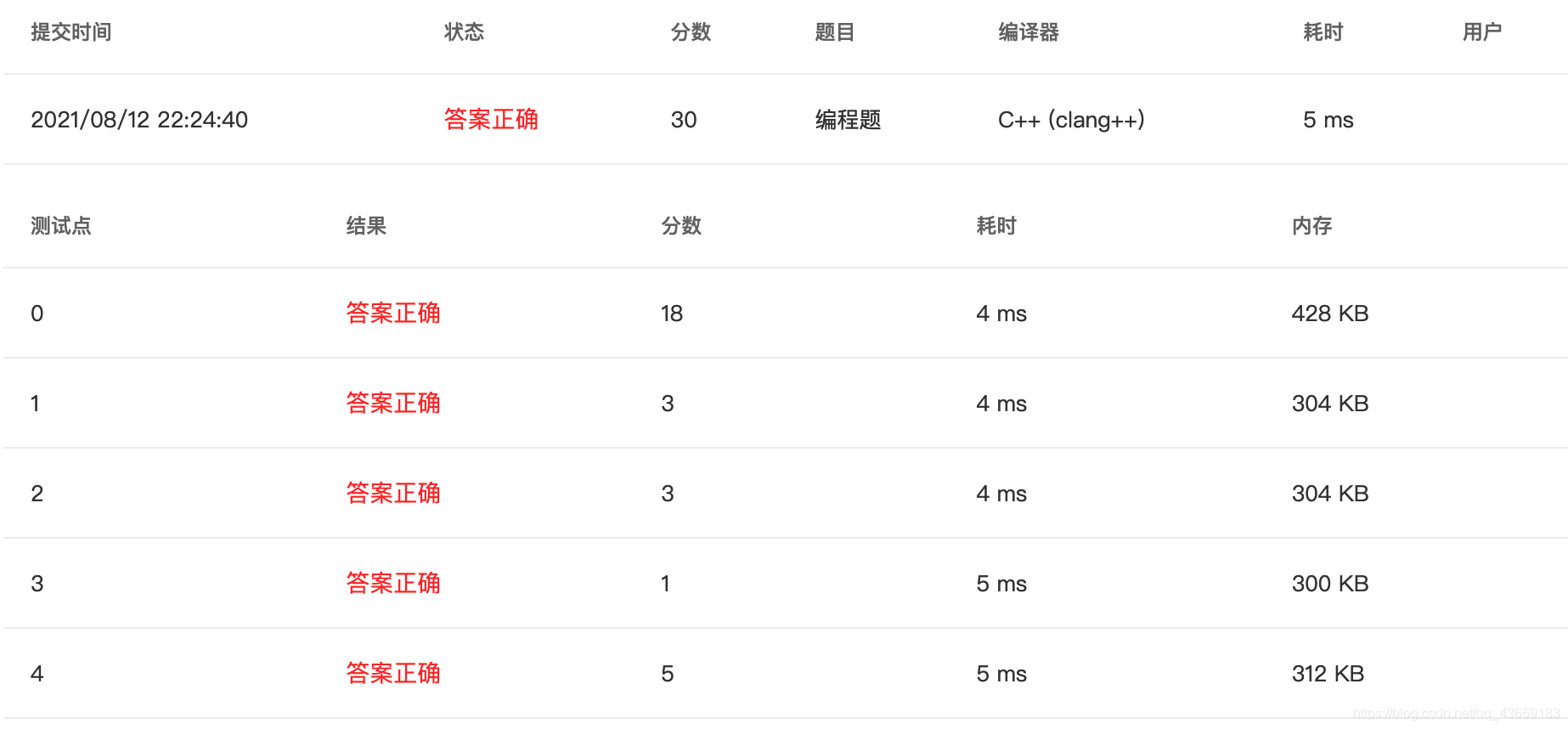
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N(\le 100)$ which is the total number of nodes in the tree. The next $N$ lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to $N?1$, and 0 is always the root. If one child is missing, then $?1$ will represent the NULL child pointer. Finally $N$ distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

Caution:

思路比较简单，先构建好树形，然后进行中序遍历，然后将输入的数组先进行排序后再按照中序遍历的顺序依次填入树中（用到的性质就是二叉搜索树的中序遍历是单调递增的）。

Solution:

// Talk is cheap, show me the code
// Created by Misdirection 2021-08-12 21:44:05
// All rights reserved.

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

vector<vector<int>> tree;

struct Node{
    int num;
    Node *left;
    Node *right;

    Node(int n = 0, Node* l = NULL, Node* r = NULL){
        num = n;
        left = l;
        right = r;
    }
    ~Node(){}
};

vector<Node*> mid;

void findChildren(Node* r){

    if(tree[r -> num][0] != -1) r -> left = new Node(tree[r -> num][0], NULL, NULL);
    if(tree[r -> num][1] != -1) r -> right = new Node(tree[r -> num][1], NULL, NULL);

    if(r -> left != NULL) findChildren(r -> left);
    if(r -> right != NULL) findChildren(r -> right);
    
    return;
}

void midOrder(Node* r){
    // if(r == NULL) return;

    // midOrder(r -> left);
    // cout << r -> num << ' ';
    // midOrder(r -> right);
    // 上面的是检查树形的时候的中序遍历代码

    // 下面的是填入 Node 指针的时候中序遍历代码

    if(r == NULL) return;
    midOrder(r -> left);
    mid.push_back(r);
    midOrder(r -> right);
}

void preOrder(Node *r){
    if(r == NULL) return;

    cout << r -> num << ' ';
    preOrder(r -> left);
    preOrder(r -> right);
}



int main(){
    int n;
    cin >> n;
    
    tree.resize(n, vector<int>(2));

    for(int i = 0; i < n; ++i) scanf("%d %d", &tree[i][0], &tree[i][1]);

    Node *root = new Node(0, NULL, NULL);
    findChildren(root);
    
    // 中序遍历和前序遍历以检查树形
    // midOrder(root);
    // cout << endl;
    // preOrder(root);
    // cout << endl;

    mid.clear();
    midOrder(root);
    
    vector<int> num(n);

    for(int i = 0; i < n; ++i) scanf("%d", &num[i]);
    sort(num.begin(), num.end());

    for(int i = 0; i < n; ++i) mid[i] -> num = num[i];
    // 检查填的对不对
    // preOrder(root);
    // cout << endl;

    // 现在层次遍历
    queue<Node*> q;
    q.push(root);

    while(!q.empty()){
        printf("%d", q.front() -> num);
        
        if(q.front() -> left != NULL) q.push(q.front() -> left);
        if(q.front() -> right != NULL) q.push(q.front() -> right);
        q.pop();

        if(q.empty()) printf("\n");
        else printf(" ");
    }

    return 0;
}