[数据结构与算法]sklearn实现线性模型

用sklearn实现各种线性回归模型，训练数据为房价预测数据，数据文件见https://download.csdn.net/download/d1240673769/20910882

加载房价预测数据

import pandas as pd 
df = pd.read_csv('sample_data_sets.csv')  # 房价预测数据 
print(df.columns)
df.head()

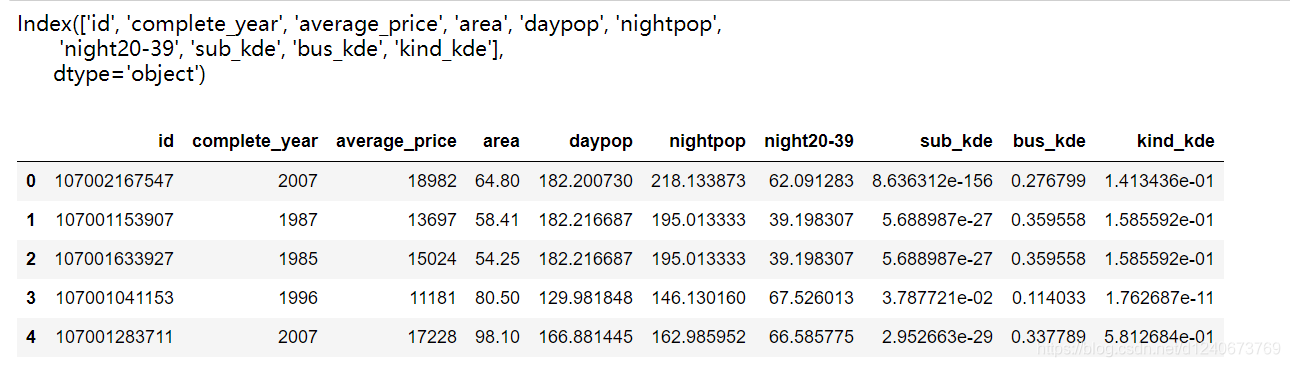
制作标签变量

# 制作标签变量
price_median = df['average_price'].median()   # 房价中位数
print(price_median)

#  定义一个是否是高房价标签（大于中位数为高房价）
df['is_high'] = df['average_price'].map(lambda x: True if x>= price_median else False)
print(df['is_high'].value_counts())

提取自变量和因变量

# 提取自变量
x_train = df.copy()[['area', 'daypop', 'nightpop',
       'night20-39', 'sub_kde', 'bus_kde', 'kind_kde']]
# 提取因变量：数值型
y_train = df.copy()['average_price']
# 提取因变量：类别型
y_label = df.copy()['is_high']

线性回归模型

# 加载pipeline
from sklearn.pipeline import Pipeline

# 加载线性回归模型
from sklearn.linear_model import LinearRegression

# 构建线性回归模型
pipe_lm = Pipeline([
        ('lm_regr',LinearRegression(fit_intercept=True))   # fit_intercept=True 表示拟合截距值
        ])

# 训练线性回归模型
pipe_lm.fit(x_train, y_train)

# 使用线性回归模型进行预测
y_train_predict = pipe_lm.predict(x_train)

# 查看线性回归模型特征参数
print(pipe_lm.named_steps['lm_regr'].coef_)

# 查看线性回归模型截距值
print(pipe_lm.named_steps['lm_regr'].intercept_)

# 提取模型特征参数
coef = pipe_lm.named_steps['lm_regr'].coef_

# 提取对应的特征名称
features = x_train.columns.tolist()

# 构建参数df
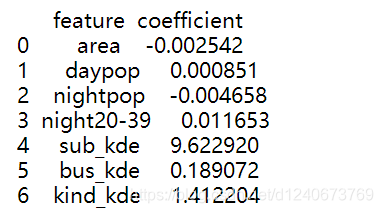
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)

# 加载画图组件matplotlib
import matplotlib.pyplot as plt
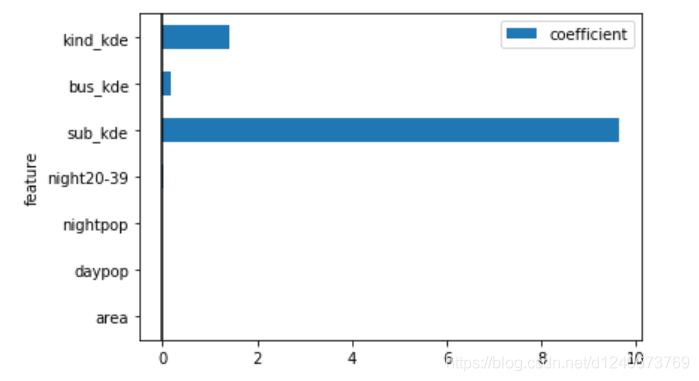
# 绘制参数特征值柱状图
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()

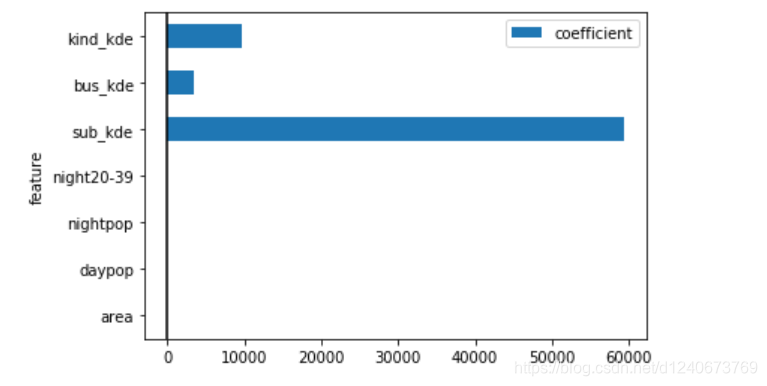
# 绘制参数特征值柱状图
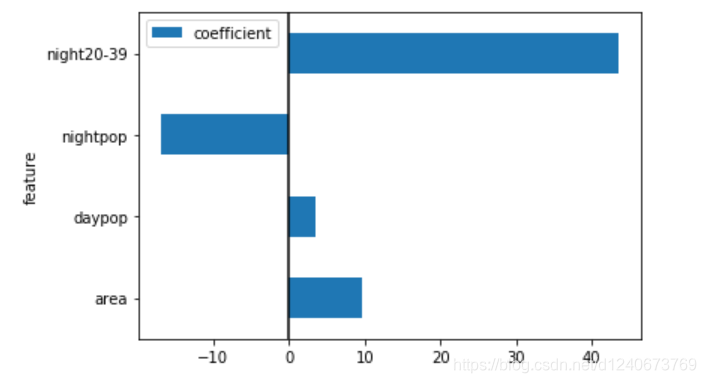
coef_table.set_index(['feature']).iloc[0:4].plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()

lasso线性回归模型

# 加载lasso回归模型
from sklearn.linear_model import Lasso

# 构建线性回归模型
pipe_lasso = Pipeline([
        ('lasso_regr',Lasso(alpha=500, fit_intercept=True))  # alpha控制L1正则系数的约束值
        ])

# 训练线性回归模型
pipe_lasso.fit(x_train, y_train)
# 使用线性回归模型进行预测
y_train_predict = pipe_lasso.predict(x_train)

# 查看线性回归模型特征参数
print(pipe_lasso.named_steps['lasso_regr'].coef_)

# 查看线性回归模型截距值
print(pipe_lasso.named_steps['lasso_regr'].intercept_)

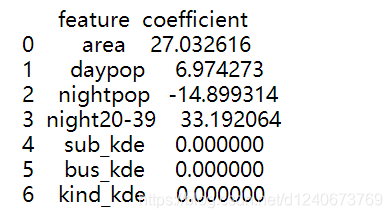
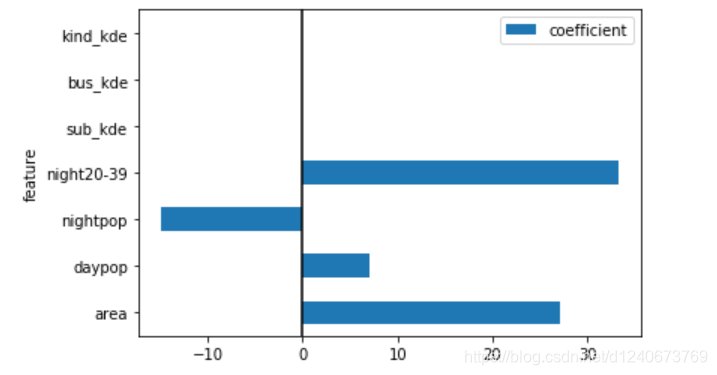
如上图：后三个特征值的参数被约束到0

# 提取模型特征参数
coef = pipe_lasso.named_steps['lasso_regr'].coef_

# 提取对应的特征名称
features = x_train.columns.tolist()

# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)

coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()

ridge线性回归模型

# 加载ridge回归模型
from sklearn.linear_model import Ridge

# 构建ridge回归模型
pipe_ridge = Pipeline([
        ('ridge_regr',Ridge(alpha=500, fit_intercept=True, solver = 'lsqr'))  # solver为求解器，lsqr表示最小二乘法
        ])

# 训练ridge回归模型
pipe_ridge.fit(x_train, y_train)
# 使用ridge回归模型进行预测
y_train_predict = pipe_ridge.predict(x_train)

# 查看ridge回归模型特征参数
print(pipe_ridge.named_steps['ridge_regr'].coef_)

# 查看ridge回归模型截距值
print(pipe_ridge.named_steps['ridge_regr'].intercept_)

# 提取模型特征参数
coef = pipe_ridge.named_steps['ridge_regr'].coef_

# 提取对应的特征名称
features = x_train.columns.tolist()

# 构建参数df
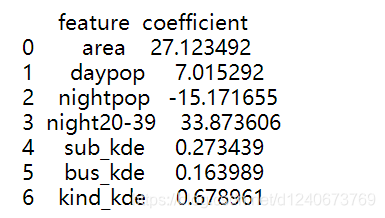
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)

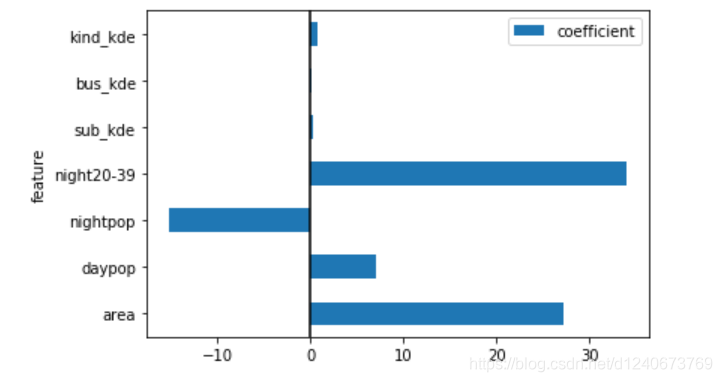
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()

logstic回归模型

# 加载logstic回归模型
from sklearn.linear_model import LogisticRegression

# 构建线性回归模型
pipe_logistic = Pipeline([
        ('logistic_clf',LogisticRegression(penalty='l1', fit_intercept=True, solver='liblinear'))
        ])
# 训练线性回归模型
pipe_logistic.fit(x_train, y_label)
# 使用线性回归模型进行预测
y_train_predict = pipe_logistic.predict(x_train)

逻辑回归模型参数解释:

penalty（默认使用l2正则系数）

• ‘l1’: l1正则系数,
• ‘l2’: l2正则系数
• ‘none’:无正则系数

solver（默认是’liblinear’:坐标下降法）

• ‘liblinear’：坐标下降法，可以处理了l1和l2正则系数，适用于小数据量（一般指10w个样本以下）
• ‘sag’：sag是随机平均梯度下降法，只能处理l2正则系数，适用于大数据量
• ‘saga’: saga是sag的变体，能处理l1和l2正则系数，适用于大数据量

# 查看逻辑回归模型特征参数
print(pipe_logistic.named_steps['logistic_clf'].coef_)

# 查看逻辑回归模型截距值
print(pipe_logistic.named_steps['logistic_clf'].intercept_)

# 提取模型特征参数
coef = pipe_logistic.named_steps['logistic_clf'].coef_[0]

# 提取对应的特征名称
features = x_train.columns.tolist()

# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)

coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()