[数据结构与算法]从头开始设计一个数据结构—堆

一、堆的定义

堆树的定义如下：
（1）堆树是一颗完全二叉树；
（2）堆树中某个节点的值总是不大于或不小于其孩子节点的值；
（3）堆树中每个节点的子树都是堆树。

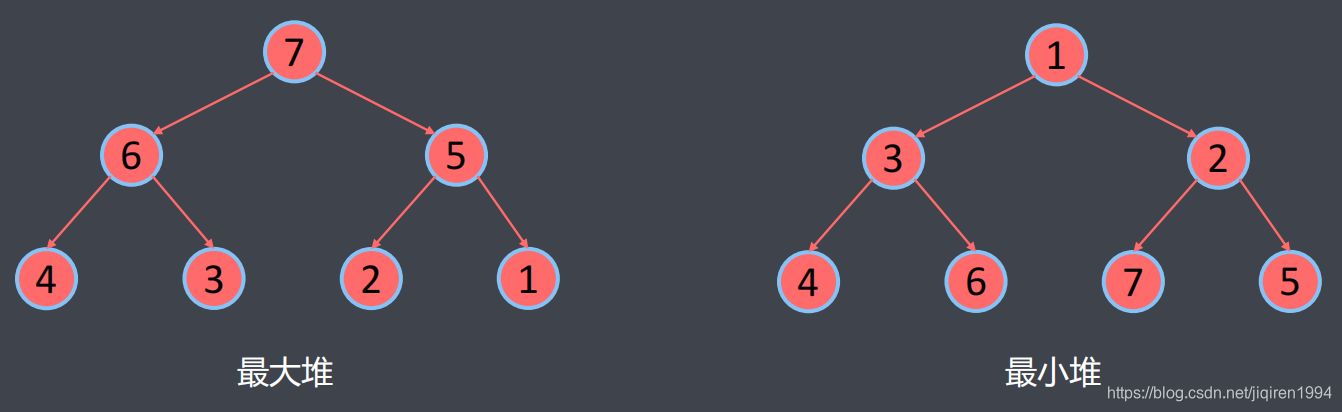
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。
当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

二、堆的特性

已知双亲(parent)的下标，则:

• 左孩子(left)下标 = 2 * parent + 1;
• 右孩子(right)下标 = 2 * parent + 2;

已知孩子(不区分左右)(child)下标，则:

• 双亲(parent)下标 = (child - 1) / 2;

三、堆的分类

当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

四、堆的操作

4.1 堆的建立

1. 倒序遍历数列，因为下标在size/2 - 1之后的节点都是叶子结点，所以可以从size/2-1位
   置开始倒序遍历，减少比较次数。
2. 对二叉树中的元素挨个进行沉降处理，沉降过程为：把遍历到的节点与左右子节点中的最小值比对，如果比最小值要大，那么和孩子节点交换数据，反之则不作处理，继续倒序遍历。
3. 沉降后的节点，再次沉降，直到叶子节点。

4.2 堆的插入

1. 新元素默认插入末尾
2. 指定最后一个元素为当前元素，执行上浮操作

4.3 堆的删除

1. 取根元素
2. 把最后一个元素赋值为根节点
3. 指定根节点为起始节点，执行下沉操作

4.4 堆的上浮

1. 以指定元素为启点
2. 比较当前节点元素与其父元素大小
3. 如果当前节点元素小于其父节点元素，则交互2个节点元素的值，把其父节点置为当前节点；否则算法结束。
4. 重复步骤2~3，直到当前节点为根元素。

4.5 堆的下沉

1. 以指定元素为启点
2. 比较当前节点元素与其子节点元素大小，取最小值
3. 如果当前节点元素为最小元素，则结束算法；如果左子节点为最小元素，则交互2个节点元素的值，把其左子节点节点置为当前节点；如果右子节点为最小元素，则交互2个节点元素的值，把其右子节点节点置为当前节点；
4. 重新获取当前节点的左右子节点
5. 重复步骤2~4，直到当前节点的左右子节点都为空。.

五、堆的实现

public class heap {
    private int [] heapArr;
    private int size=0;
    public heap(){
        heapArr=new int[8];
    }
    public heap(int num){
        heapArr=new int[num];
    }
    public heap(int [] arr){
        heapArr=arr;
        build(arr);
    }

    /**
     * 1.从最后一个父节点开始进行沉降即可
     * @param arr
     */
    private void build(int [] arr){
        for(int i=arr.length/2 - 1;i>=0;i--){
            sinkDown(i);
        }
    }

    /**
     * 1.插入到最后的那个元素,如果大小已经和数组一样大，则进行扩容
     * 2.执行元素校验，检查插入元素是否符合堆的特性，不符合则进行调整，插入采用上浮操作
     */

    public void insert(int des){
        if(size>=heapArr.length){
            resize();
        }
        heapArr[size]=des;
        floatUp(size);
        size++;
    }

    /**
     * 1.交换堆底元素与堆顶元素，为了保持堆的完全二叉树结构，从底部交换方便处理一些
     * 2.弹出堆底部元素，从对顶开始下沉
     */
    public int pop(){
        int temp=heapArr[0];
        heapArr[0]=heapArr[size];
        size--;
        //下沉
        sinkDown(0);
        return temp;
    }
    public void resize(){
        heapArr= Arrays.copyOf(heapArr, heapArr.length*2);
    }

    /**
     * 大顶堆，父元素最大
     * 小顶堆，父元素最小
     * 我们以小顶堆为例
     * 1.与父元素比较，双亲(parent)下标 = (child - 1) / 2;
     * 2.交换两者的位置
     * 3.检查父元素是否符合要求
     * @param index
     */
    private void floatUp(int index){

        if(index<0){
            return;
        }
        int parent=(index-1)/2;
        if(heapArr[parent]>heapArr[index]){
           int temp=heapArr[parent];
           heapArr[parent]=heapArr[index];
           heapArr[index]=temp;
           //检查父元素是否符合要求
            floatUp(parent);
        }
    }

    /**
     * 大顶堆，父元素最大
     * 小顶堆，父元素最小
     * 我们以小顶堆为例
     * 左孩子(left)下标 = 2 * parent + 1;
     * 右孩子(right)下标 = 2 * parent + 2
     *
     * 1.检查两个子元素与父元素比较
     *
     * @param parent
     */
    private void sinkDown(int parent){
        if(parent<0){
            return;
        }

        int leftChild=2 * parent + 1;
        int rightChild=2 * parent + 2;

        int minIndex;
        if(heapArr[leftChild]>heapArr[rightChild]){
            minIndex=rightChild;
        }else{
            minIndex=leftChild;
        }
        //父元素大于子元素的话则进行交换
        if(heapArr[parent]>heapArr[minIndex]){
            int temp=heapArr[parent];
            heapArr[parent]=heapArr[minIndex];
            heapArr[minIndex]=temp;
            sinkDown(minIndex);
        }

    }
}