[数据结构与算法]数据结构与算法_【8】图（C++实现）

参考：数据结构与算法基础（青岛大学-王卓）
传送门：
数据结构与算法_【1】概念引入（C++实现）
数据结构与算法_【2】线性表（顺序表链表）（C++实现）
数据结构与算法_【3】栈和队列（C++实现）
数据结构与算法_【4】串数组广义表（C++实现）
数据结构与算法_【5】树和二叉树（C++实现）
数据结构与算法_【6】树和森林（C++实现）
数据结构与算法_【7】哈夫曼树（C++实现）
数据结构与算法_【8】图（C++实现）

图

数据的逻辑结构：
集合：数据元素间除“同属于一个集合外”，无其他关系
线性结构：一对一，如线性表、栈、队列
树形结构：一对多，如树
图形结构：多对多，如图

1 图的定义和基本术语

图：G=（V，E） Group = （Vertex，Edge）
V：顶点（数据元素）的有穷非空集合
E：边的有穷集合

无向图： 每条边都是无方向的
有向图： 每条边都是有方向的
完全图： 任意两个点都有一条边相连
稀疏图： 有很少边或弧的图（e<nlogn）
稠密图： 有较多边或弧的图
网： 边/弧带权的图
邻接： 有边/弧相连的两个顶点之间的关系，存在（vi，vj），则称vi，vj互为邻接点；存在< vi，vj >，则称vi邻接到vj，vj邻接于vi
关联（依附）： 边/弧与顶点之间的关系，存在（vi，vj）/< vi，vj >，则称该边/弧关联于vi和vj
顶点的度： 与该顶点相关联的边的数目，记作TD(v)，在有向图中，顶点的度等于该顶点的入度与出度之和，顶点v的出度是以v为终点的有向边的条数，记作ID(v)，顶点v的出度是以v为始点的有向边的条数，记作OD(v)

当有向图中仅一个顶点的入度为0，其余顶点的入度为1，此时是何形状？ ---->树

路径： 接续的边构成的顶点序列
路径长度： 路径上边或弧的数目/权值之和
回路（环）： 第一个顶点和最后一个顶点相同的路径
简单路径： 除路径起点和终点 可以 相同外，其余顶点均不相同的路径
简单回路（简单环）： 除路径起点和终点相同外，其余顶点均不相同的路径

连通图（强连通图）：

权与网： 图中边或弧所具有的相关数称为权；表明从一个顶点到另一个顶点的距离或耗费；带权的图称为网
子图：

连通分量（强连通分量）：

有向图中存在强连通分量

极小连通子图： 该子图是G的连通子图，在该子图中删除任何一条边，子图不再连通
生成树： 包含无向图G所有顶点的极小连通子图
生成森林： 对非连通图，由各个连通分量的生成树的集合

2 图的类型定义

3 图的存储结构

图的逻辑结构：多对多

图没有顺序存储结构，但是可以借助二维数组来表示元素间的关系
数组表示法（邻接矩阵）

链式存储结构
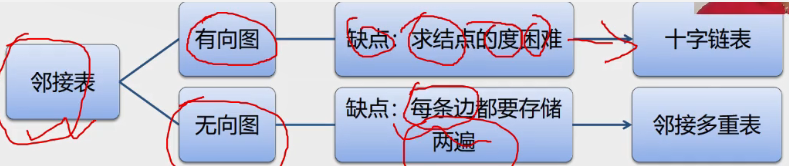
多重链表：邻接表、邻接多重表、十字链表

重点介绍：邻接矩阵（数组）表示法；邻接表（链式）表示法

3.1 邻接矩阵（数组表示法）

无向图例子：

分析1：无向图的邻接矩阵是对称的
分析2：顶点i的度=第i行（列）中1的个数
特别：完全图的邻接矩阵中，对角元素为0，其余为1

有向图例子：

网（有权图）的邻接矩阵表示法：

3.2 邻接矩阵存储表示

代码：

#pragma once
#include<iostream>
using namespace std;
#define MaxInt 32767
#define MVNum 100

class AMGraph {
private:
	char vexs[MVNum];//顶点表
	int arcs[MVNum][MVNum];//邻接矩阵
	int _vexnum, _arrnum;//图的当前点树和边数
public:
	AMGraph() {}//默认构造
	AMGraph(int vexnum, int arrnum);//构造函数
	int LocateVex(char v);//返回结点v在所有结点中的位置，以此推断邻接表的位置
	void CreateAMGraph();
	void ShowAMGraph();

};

AMGraph::AMGraph(int vexnum, int arrnum)
{
	this->_vexnum = vexnum;
	this->_arrnum = arrnum;
	
	//输入结点信息
	cout << "请输入结点信息：" << endl;
	for (int i = 0; i < this->_vexnum; i++)
	{
		cout << "请输入第" << i + 1 << "个结点：" << endl;
		cin >> this->vexs[i];
	}
	cout << "顶点表初始化完毕！" << endl;
	//给邻接矩阵赋初值
	for (int i = 0; i < this->_vexnum; i++)
	{
		for (int j = 0; j < this->_vexnum; j++)
		{
			this->arcs[i][j] = MaxInt;
		}

	}
	cout << "邻接矩阵初始化完毕！" << endl;

	system("pause");
	system("cls");

}

int AMGraph::LocateVex(char v)
{
	//cout << "111" << endl;
	for (int i = 0; i < this->_vexnum; i++)
	{
		if (v == this->vexs[i])
		{
			return i;
		}
	}
	cout << "位置寻找错误！返回-1！" << endl;
	return -1;
}

void AMGraph::CreateAMGraph()
{
	cout << "请输入邻接矩阵信息（v1，v2，w）用空格分割：" << endl;
	for (int j = 0; j < this->_arrnum; ++j)
	{
		char v1, v2;
		int w;
		cout << "请输入第" << j + 1 << "条结点信息：" << endl;
		cin >> v1 >> v2 >> w;

		int a = this->LocateVex(v1);
		int b = this->LocateVex(v2);
		this->arcs[a][b] = w;
		this->arcs[b][a] = this->arcs[a][b];//无向图邻接矩阵对称
	}
	cout << "邻接矩阵构建完毕！" << endl;
	this->ShowAMGraph();
	system("pause");
	system("cls");
}

void AMGraph::ShowAMGraph()
{
	cout << "\t";
	for (int k = 0; k < this->_vexnum; k++)
	{
		cout << this->vexs[k] << "\t";
	}
	cout << endl;

	for (int i = 0; i < this->_vexnum; i++)
	{
		cout << this->vexs[i] << "\t";
		for (int j = 0; j < this->_vexnum; j++)
		{
			cout << this->arcs[i][j] << "\t";
		}
		cout << endl;
	}
}

邻接矩阵优点：

邻接矩阵缺点：

3.3 邻接表（链式）

无向图邻接表

无向图邻接表特点：
（1）邻接表不唯一
（2）若无向图中有n个顶点，e条边，则其邻接表需n个头结点和2e个表结点。适宜存储稀疏图。
（3）无向图中顶点vi的度为第i个单链表中的结点数

有向图邻接表

算法思想：

代码：

#pragma once
#include<iostream>
using namespace std;

#define MVNum 100

class ArcNode;

class VNode {
public:
	char data;//结点名称
	ArcNode* firstarc;//指向第一个边结点的指针
};

class ArcNode {
public:
	int adjvex;//该边所指向的顶点的位置
	ArcNode* nextarc = NULL;//指向下一条边的指针
	int ifo;//和边相关的信息（权值）
};


class ATGraph {
private:
	VNode* vertex;//指向邻接表的头指针
	int _vexnum, _arcnum;
public:
	ATGraph(int vexnum, int arcnum);
	void CreatATGraph();//创建图
	int LocateVex(char v);//定位结点位置
	void ShowATGraph();


};

ATGraph::ATGraph(int vexnum, int arcnum)
{
	this->_vexnum = vexnum;
	this->_arcnum = arcnum;
	this->vertex = new VNode[vexnum];//给邻接表分配空间
	//输入结点信息
	cout << "请输入结点信息：" << endl;
	for (int i = 0; i < this->_vexnum; i++)
	{
		cout << "请输入第" << i + 1 << "个结点：" << endl;
		cin >> this->vertex[i].data;
		this->vertex[i].firstarc = NULL;
	}
	cout << "顶点表初始化完毕！" << endl;
	system("pause");
	system("cls");

}


int ATGraph::LocateVex(char v)
{
	for (int i = 0; i < this->_vexnum; i++)
	{
		if (v == this->vertex[i].data)
		{
			return i;
		}
	}
	cout << "位置寻找错误！返回-1！" << endl;
	return -1;
}

void ATGraph::CreatATGraph()
{
	cout << "请输入邻接矩阵信息（v1，v2，w）用空格分割：" << endl;
	for (int j = 0; j < this->_arcnum; ++j)//需要输入的边的个数
	{
		char v1, v2;
		int w;
		cout << "请输入第" << j + 1 << "条结点信息：" << endl;
		cin >> v1 >> v2 >> w;

		int a = this->LocateVex(v1);
		int b = this->LocateVex(v2);

		//无向网，所以要操作两次
		ArcNode* p1 = new ArcNode;//申请一个存储边结点的空间
		p1->adjvex = b;//邻接点的序号为b
		p1->ifo = w;
		p1->nextarc = this->vertex[a].firstarc;
		this->vertex[a].firstarc = p1;

		//若有向网，则下面可以省略！
		ArcNode* p2 = new ArcNode;//申请一个存储边结点的空间
		p2->adjvex = a;//邻接点的序号为b
		p2->ifo = w;
		p2->nextarc = this->vertex[b].firstarc;
		this->vertex[b].firstarc = p2;

	}
	cout << "邻接矩阵构建完毕！" << endl;
	this->ShowATGraph();
	system("pause");
	system("cls");

}

void ATGraph::ShowATGraph()
{
	
	for (int i = 0; i < this->_vexnum; i++)
	{

		cout << this->vertex[i].data << "\t";
		ArcNode* p = this->vertex[i].firstarc;
		while (p != NULL)
		{
			cout << p->adjvex <<" "<<p->ifo<< "\t";
			p = p->nextarc;
		}

		cout << endl;

	}
}

邻接表特点：

3.4 邻接矩阵和邻接表对比

邻接矩阵多用于稠密图，而邻接表多用于稀疏图。

3.5 十字链表和邻接多重表

4 图的遍历

遍历定义： 从已给的连通图中某一顶点出发，沿着一些边访遍图中所有顶点，且每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算。
遍历实质： 找每个顶点邻接点的过程
图的特点：

常用的遍历：
（1）深度优先搜索DFS

邻接矩阵表示的无向图深度遍历实现：

void AMGraph::DFS(int v, int* visited)
{
	cout << this->vexs[v] << endl;
	visited[v] = 1;
	for (int i = 0; i < this->_vexnum; i++)
	{
		if (this->arcs[v][i] != 0 && (visited[i] != 1))
		{
			this->DFS(i, visited);
		}
	}
}

测试：

不同存储方式 图的遍历比较：

（2）广度优先搜索BFS

邻接表实现BFS：

邻接表表示的无向图广度遍历实现：
所用到的队列在之前的笔记中给出了实现代码：数据结构与算法_【3】栈和队列（C++实现）

void ATGraph::BFS(int v, int* visited)//非递归
{
	cout << this->vertex[v].data << endl;//先打印第v个顶点
	visited[v] = 1;//将此顶点记录为1，后面不再访问
	SeqQueue<int> SQ;
	SQ.EnQueue(v);
	while (!SQ.QueueEmpty())
	{
		int temp;
		SQ.DeQueue(temp);
		//遍历每个顶点后的邻域结点
		for (ArcNode* p = this->vertex[temp].firstarc; p != NULL; p = p->nextarc)
		{
			int i = p->adjvex;
			if (visited[i] == 0)
			{
				cout << this->vertex[i].data << endl;
				visited[i] = 1;
				SQ.EnQueue(i);
			}
		}
	}
}

DFS和BFS算法比较：

5 图的应用

5.1 最小生成树

生成树：所有顶点均由边连接在一起，但不存在回路的图。

无向图的生成树：

最小生成树：

MST性质：

构造最小生成树方法一：普里姆（Prim）算法

构造最小生成树方法一：克鲁斯卡尔（Kruskal）算法

两种算法比较：

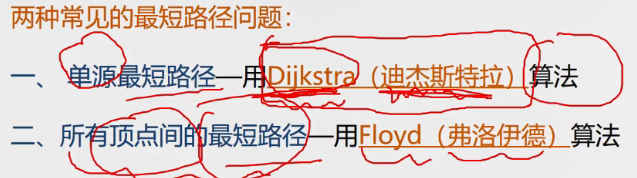
5.2 最短路径

Dijkstra（迪杰斯特拉算法）

Floyd（弗洛伊德算法）

5.3 拓扑排序

有向无环图：

两种网：

AOV网：

拓扑排序：

5.4 关键路径

案例分析：